Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration finite foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Chern character

Bottom of Page

1 to 44 of 44

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeJan 5th 2010

    stub for Chern character

    just the blind definition so far, to be expanded later

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeJan 7th 2010
    • (edited Jan 7th 2010)

    added now the full abstract-nonsense definition to Chern character

    well, or at least I indicate it . The key ingredient is the notion of "fundamental cocycle" on a spectrum. For that I currently just point to page and verse in the literature.

    This is also in reply to my discussion, elswewhere, with Domenico: that fundamental cocycle is essentially (in a special case) that morphism 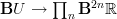\mathbf{B}U \to \prod_n \mathbf{B}^{2n} \mathbb{R} that I kept mentioning.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeJan 7th 2010

    created stub for curvature since I couldn't stand the unsatisfied hyperlinks anymore.

    But nothing substantially there yet.

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeJan 7th 2010

    I couldn't help it:

    now some genuine content at curvature: an "Idea"-section and a section on curvatures of trivial bundles (i.e. of differential forms).

    • CommentRowNumber5.
    • CommentAuthorzskoda
    • CommentTimeJan 7th 2010

    What is k_j in the formula ?

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeJan 7th 2010
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> What is <img src="/extensions/vLaTeX/cache/latex_cd21992f62780aa6e561f8f7874c8326.png" title="k_j" style="vertical-align: -20%;" class="tex" alt="k_j"/> in the formula ? </blockquote> <p>I have now put in the value of <img src="/extensions/vLaTeX/cache/latex_cd21992f62780aa6e561f8f7874c8326.png" title="k_j" style="vertical-align: -20%;" class="tex" alt="k_j"/> following the first source on my desk that I can reach right now, which is <a href="http://ncatlab.org/nlab/show/Simons-Sullivan+structured+bundle">Simons-Sullivan</a>:</p> <p><a href="http://ncatlab.org/nlab/show/Chern+character#KTheory">here</a> is the new version</p> <p>But eventually I'd like to sort this out in a dedicated entry on characteristic classes.</p> </div>
    • CommentRowNumber7.
    • CommentAuthorzskoda
    • CommentTimeJan 7th 2010
    • (edited Jan 7th 2010)

    Thanks. The entry is nicely growing. I think it may be dangerous to call K-theory spectrum by somewhat nonstandard notation KU. I hope we will be able to connect to the standard discussion relating the Chern classes and consequently the Chern character to the business of lambda-rings.

    Cf. blog.

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeJan 7th 2010

    I have to run now. You are right about the notation. Maybe you could inprove it.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010

    I admit that it's something like my third attempt, but I do have a good guess now for the fully general abstract notion of

    Chern character in an (oo,1)-topos

    • CommentRowNumber10.
    • CommentAuthorzskoda
    • CommentTimeFeb 19th 2010

    wow

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010
    • (edited Feb 19th 2010)

    I am now beginning to see much clearer. One just has to use formal topos theory reasoning systematically to see all the structure.

    Here is the next one: I think I understand now also the "infinitesimal path oo-groupoid" functor fully intrinsically:

    recall that non-intrinsically I construct this in the oo-topos of oo-stacks on the site whose objects are infinitesimally thickened cartesian spaces. There is the the obvious site map

    Red : CartSp_{thick} \to CartSp

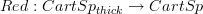
    that forgets the infinitesimal thickening. This should induce an essential geometric morphisms of oo-topos, and the left-left adjoint of that is Pi_inf.

    So intrinsically, what I really want to say is that:

    oo-Lie theory is the cohomology in a relative oo-topos, namely one oo-topos sitting over another by an essential geometric morphism

    \mathbf{K} \to \mathbf{H}

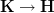
    which is such that it remembers that 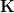\mathbf{K} is an "infinitesimal thickening" of \mathbf{H} .

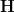    So I think what I need is the gros oo-topos-theortic version of a formal scheme sitting over its underlying scheme, or the like.

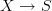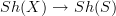    What's the abstract way to say this, in the classical theory: if S is a scheme and X an infinitesimal thickening of S with projection X \to S , let Sh(X) \to Sh(S) be the corresponding geometric morphism of sheaf toposes. Which property of this geometric morphism is it that remembers that X was not just any scheme over S, but an infintesimal thickening?

    • CommentRowNumber12.
    • CommentAuthorzskoda
    • CommentTimeFeb 19th 2010

    I like this about relative point of view to Lie theory. This could explain Lie theory for (algebras over) other operads (see papers by Fresse), which was the motivation of original 1992 Kontsevich work on formal noncommutative symplectic geometry and Ginzburg-Kapranov on Koszul duality for operads about the same time.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010

    Concerning the question how to characterize topos morphisms 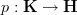p : \mathbf{K} \to \mathbf{H} that characterize infinitesimal thickenings

    I was going to suggest that the condition should be that on topos points the morphism 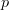p induces a bijection, i.e. that 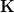\mathbf{K} may be bigger than 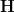\mathbf{H} but not have further genuine points.

    But somehow that does not seem to work here: the points of 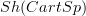Sh( CartSp ) (or Sh(Diff) for that matter) are the stalks on disks, so there is one per natural number. But 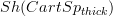Sh(CartSp_{thick}) seems to have a point per "disk times a choice of infinitesimal thickening".

    Hm...

    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010

    ah, wait, I am overl0oking something: those "infinitesimal stalks" don't preserve finte limits, right? so they don't give topos points.

    aha, so the condition might be right after all...

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeMar 10th 2010

    added a reference to Chern character

    • CommentRowNumber16.
    • CommentAuthorzskoda
    • CommentTimeJul 16th 2010

    I expanded somewhat Chern-Weil theory. Please check.

    • CommentRowNumber17.
    • CommentAuthorUrs
    • CommentTimeJul 16th 2010

    added links. Notice we also have Weil homomorphism

    have to run now…

    • CommentRowNumber18.
    • CommentAuthorzskoda
    • CommentTimeJul 16th 2010

    I think people say Chern-Weil homomorphism more often. Currently Chern-Weil homorphism redirects to Chern-Weil theory. Having also Weil homomorphism, some suboptimality of organization may be detected.

    • CommentRowNumber19.
    • CommentAuthorKevin Lin
    • CommentTimeJul 20th 2010
    Things to be added (by me later, or by someone else sooner): Something about (Grothendieck-)Hirzebruch-Riemann-Roch. Something about the Chern character at the level of formal group laws. Some other stuff from this MO post would be nice too.
    • CommentRowNumber20.
    • CommentAuthorzskoda
    • CommentTimeJul 20th 2010

    It is difficult to go to the bottom when Riemann-Roch theorems are considered. In other words it is difficult to take NPOV as the subject is still not well understood. I mean all the proofs are still a hack (in agreement with Grothendieck’s unsatisfaction with his own proof, published by Jean-Pierre Serre). So please be careful when writing, it is easy to make a mess in such a difficult topic.

    • CommentRowNumber21.
    • CommentAuthorKevin Lin
    • CommentTimeJul 20th 2010
    OK.

    I haven't read any of it beyond the abstract, but this paper of Toen might be in the right direction?
    • CommentRowNumber22.
    • CommentAuthorKevin Lin
    • CommentTimeJul 20th 2010
    Is the goal [in general, or of nCafe/nLab/nForum] to make everything fit into the nPOV?
    • CommentRowNumber23.
    • CommentAuthorEric
    • CommentTimeJul 20th 2010

    Is the goal [in general, or of nCafe/nLab/nForum] to make everything fit into the nPOV?

    Maybe some answers: nPOV

    • CommentRowNumber24.
    • CommentAuthorUrs
    • CommentTimeJul 20th 2010
    • (edited Jul 20th 2010)

    Is the goal [in general, or of nCafe/nLab/nForum] to make everything fit into the nPOV?

    No. We want all the good content that we can get. But we take the liberty of allowing us to afterwards go through it and reformulate some of it from the nPOV.

    If you feel energetic, don’t let the nPOV issue stop you from adding stuff. Just create a a subsection with a descrptive title and go.

    • CommentRowNumber25.
    • CommentAuthorzskoda
    • CommentTimeJul 20th 2010

    I took nPOV in the widest possible sense of a natural proof. So far such a proof of Grothendieck-Riemann-Roch has not being found. I know a couple of people who have some insight in the right direction but did not get to the bottom yet.

    • CommentRowNumber26.
    • CommentAuthorTodd_Trimble
    • CommentTimeJul 20th 2010

    Zoran, I’m not sure I understand why you are being so fussy here. Rhetorical question: is every page you write perfectly polished and written with great care, with proofs in conformance with nPOV as you understand the term?

    If Kevin is motivated to write something on Grothendieck-Hirzebruch-Riemann-Roch, then by all means he should proceed full steam ahead, without worrying about whether he (or Grothendieck) has really gotten to the bottom of it according to Zoran. As we all know, nLab pages generally improve over time anyway (with the help of people like Zoran).

    • CommentRowNumber27.
    • CommentAuthorzskoda
    • CommentTimeJul 20th 2010
    • (edited Jul 20th 2010)

    My past experience is that writing a neutral information like references and so on, is harmless, but writing complicated tricky section once done wrong way is very hard to improve (read takes more time to imrpove than to write from the beginning), especially when you care not to hurt the structure from your predecessor (in fact a number of pages where I could contribute I never did just because there are too difficult to tackle, being created in difficult style to start with). So I absolutely did not ask not to write but asked for the care; this is one of the most important entreis. One of the voluems of SGA is dedicated solely to Riemann-Roch. I have created most of the entries on algebraic geometry in nlab and of course would like help from new people, but with similar care and dilligence – so what is wrong with the warning – spent several months last Winter and Spring preparing some grounds on the related circle of questions in nlab e.g. the very related topic of index theory (e.g. entry Fredholm operator), then bibliography stubs like slope filtration, just to have some grounds. I could of course just go to the middle of the topic and write uncarefully rambling statements but this I would not dare.

    I hoped Kevin will write but with care as the topic is tricky. For example, at the most trivial level talking Grothendieck-Hirzebruch-Riemann-Roch is already strange. There is Hirzebruch-Riemann-Roch and there is Grothendieck-Riemann-Roch, the first is corollary of the second in those setups where both apply. In some geometric situations one has HRR but not GHR, as the stronger version does not hold or is difficult to prove or even formulate. There is no Grothendieck-Hirzebruch-Riemann-Roch and I hope it will not appear as an artifact of nlab.

    • CommentRowNumber28.
    • CommentAuthorKevin Lin
    • CommentTimeJul 20th 2010
    • (edited Jul 20th 2010)
    I suppose I should not write about this topic, then, as I am clearly not as expert as Zoran... (This is not a sarcastic comment, rather it's a meek one by a dilettante.)

    I had thought that GHRR was just another name for GRR. My apologies if this is incorrect; I came to this impression after reading the wikipedia entry for "GHRR".
    • CommentRowNumber29.
    • CommentAuthorzskoda
    • CommentTimeJul 20th 2010
    • (edited Jul 20th 2010)

    No, on the contrary, I believe that you have more practical experience with RH than I do. I am on foundational side in algebraic geometry so I just talk more and think more on the foudnational aspect. But I do very little hands on algebraic geometry.

    The wikipedia article is quite good. I would be careful not to merge GRH and HRH for the simple reason that these are two different statements. GRH implies HRH in the situations in which GRH applies.

    • CommentRowNumber30.
    • CommentAuthorUrs
    • CommentTimeApr 28th 2014
    • (edited Apr 28th 2014)

    I have expanded the Idea-section at Chern character; rewording (making more succinct, basically) the statement about the Chern-character on generalized (Eilenberg-Steenrod) cohomology and adding its generalization to the Chern character in cohesion, given by the shape of the Maurer-Cartan form:

    ch E=Πθ E^ ch_{E} = \Pi \theta_{\hat E}

    with pointers to Bunke et al, where this is proven.

    Maybe I find time to further exand later.

    • CommentRowNumber31.
    • CommentAuthorUrs
    • CommentTimeAug 16th 2020

    made explicit that the EE-Chern character in Hopkins-Singer is based on the “Dold-Chern character”, made that term redirect here, and added some references on it:

    • Albrecht Dold, Relations between ordinary and extraordinary homology, Matematika, 9:2 (1965), 8–14; Colloq. algebr. Topology, Aarhus Universitet, 1962, 2–9 (mathnet:mat350), reprinted in: J. Adams & G. Shepherd (Authors), Algebraic Topology: A Student’s Guide (London Mathematical Society Lecture Note Series, pp. 166-177). Cambridge: Cambridge University Press (doi:10.1017/CBO9780511662584.015)

    • Yuli Rudyak, II.7.13 in: On Thom Spectra, Orientability, and Cobordism, Springer 1998 (doi:10.1007/978-3-540-77751-9)

    • {#Upmeier14} Markus Upmeier, Refinements of the Chern-Dold Character: Cocycle Additions in Differential Cohomology, J. Homotopy Relat. Struct. 11, 291–307 (2016). (arXiv:1404.2027, doi:10.1007/s40062-015-0106-y)

    • {#Gross19} Jacob Gross, The homology of moduli stacks of complexes (arXiv:1907.03269)

    diff, v38, current

    • CommentRowNumber32.
    • CommentAuthorDavidRoberts
    • CommentTimeAug 16th 2020
    • (edited Aug 16th 2020)

    What’s with the random ’spring’ in here ?

    • CommentRowNumber33.
    • CommentAuthorUrs
    • CommentTimeAug 16th 2020

    I had removed it, but the redirects-bug keeps it around: It’s not in the source :-)

    • CommentRowNumber34.
    • CommentAuthorUrs
    • CommentTimeAug 16th 2020

    added pointer to

    where the nature of Chern-Dold is made fully explicit.

    diff, v40, current

    • CommentRowNumber35.
    • CommentAuthorUrs
    • CommentTimeAug 16th 2020
    • (edited Aug 16th 2020)

    In the section For spectra and generalized cohomology (here) I have tried to make more explicit what is going on, and which authors find which words for this situation:

    For EE a spectrum and E •E^\bullet the generalized cohomology theory it represents

    E •(X)≃π −•Maps(X,E) E^\bullet(X) \;\simeq\; \pi_{-\bullet} Maps(X,E)

    the EE-Chern-character or Chern-Dold character for EE is simply the map induced by rationalization over the real numbers

    E⟶L ℝE ℝ E \overset{L_{\mathbb{R}}}{\longrightarrow} E_{\mathbb{R}}

    i.e. is

    labelChernDoldCharacterchd:E •(X)≃π −•Maps(X,E)⟶π −•Maps(X,L ℝ)π −•Maps(X,E ℝ)≃E 𝔼 •(X)≃H •(X,π •(E)⊗ ℤℝ). \label{ChernDoldCharacter} chd \;\colon\; E^\bullet(X) \;\simeq\; \pi_{-\bullet}Maps(X,E) \overset{ \pi_{-\bullet}Maps(X,L_{\mathbb{R}}) }{\longrightarrow} \pi_{-\bullet}Maps(X,E_{\mathbb{R}}) \;\simeq\; E^\bullet_{\mathbb{E}}(X) \;\simeq\; H^\bullet(X, \pi_{\bullet}(E)\otimes_{\mathbb{Z}}\mathbb{R}) \,.

    The very last equivalence in (eq:ChernDoldCharacter) is due to Dold 56 (reviewed in detail in Rudyak 98, II.3.17, see also Gross 19, Def. 2.5).

    One place where this neat state of affairs (eq:ChernDoldCharacter) is made fully explicit is Lind-Sati-Westerland 16, Def. 2.1. Many other references leave this statement somewhat in between the lines (e.g. Upmeier 14) and, in addition, often without reference to Dold (e.g. Hopkins-Singer 02, Sec. 4.8, Bunke 12, Def. 4.45, Bunke-Gepner 13, Def. 2.1, Bunke-Nikolaus 14, p. 17)

    Beware that some authors say Chern-Dold character for the full map in (eq:ChernDoldCharacter) (e.g. Upmeier 14, Lind-Sati-Westerland 16, Def. 2.1), while other authors mean by this only that last equivalence in (eq:ChernDoldCharacter) (eq. Rudyak 98, II.3.17, Gross 19, Def. 2.5).

    diff, v40, current

    • CommentRowNumber36.
    • CommentAuthorUrs
    • CommentTimeAug 16th 2020
    • (edited Aug 16th 2020)

    added pointer to

    • V. M. Buchstaber, The Chern–Dold character in cobordisms. I, Mat. Sb. (N.S.), 1970 Volume 83(125), Number 4(12), Pages 575–595 (mathnet:3530)

    diff, v40, current

    • CommentRowNumber37.
    • CommentAuthorUrs
    • CommentTimeAug 27th 2020

    have added pointer to Atiyah-Hirzebruch, and organized the references in two subsections, one for Chern char on K-theory, one for Chern-Dold char on generalized cohomology

    diff, v42, current

    • CommentRowNumber38.
    • CommentAuthorUrs
    • CommentTimeAug 29th 2020

    added pointer to

    (has this been published?)

    diff, v43, current

    • CommentRowNumber39.
    • CommentAuthorUrs
    • CommentTimeAug 29th 2020

    added pointer to

    both for the Chern character on K-theory, and for the Chern-Dold character, and for the proof that the latter reduces to the former

    diff, v43, current

    • CommentRowNumber40.
    • CommentAuthorUrs
    • CommentTimeAug 29th 2020

    added the original references on the Chern character in K-theory:

    diff, v43, current

    • CommentRowNumber41.
    • CommentAuthorUrs
    • CommentTimeSep 24th 2020

    added pointer to:

    diff, v45, current

    • CommentRowNumber42.
    • CommentAuthorUrs
    • CommentTimeSep 25th 2020

    added pointer to:

    • Wolfgang Lück, Chern characters for proper equivariant homology theories and applications to K- and L-theory, Journal für die reine und angewandte Mathematik, Volume 2002: Issue 543 (doi:10.1515/crll.2002.015, pdf)

    diff, v46, current

    • CommentRowNumber43.
    • CommentAuthorUrs
    • CommentTimeOct 4th 2020

    added pointer to:

    diff, v48, current

    • CommentRowNumber44.
    • CommentAuthorUrs
    • CommentTimeDec 6th 2020

    added pointer to:

    diff, v51, current

1 to 44 of 44

  1.