nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Discussion Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 10th 2010
- (edited Oct 14th 2012)
I started to greatly expand the entry module
The new toc now looks like this:
Idea
Basic idea
More general perspectives
Enriched presheaves
Stabilized overcategories
Details
Ordinary concept
In enriched category theory
Examples
- Modules over rings
Related concepts
- Vector bundles and sheaves of modules
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 10th 2010
I am in the process of adding more stuff:
in the subsection As stabilized overcategories the beginning of the proof of what is apparently originally Quillen's identification of modules with abelian group objects in the overcategory
in the subsection Examples: modules over rings more details on the standard definition of ring modules
in the subsection Examples: modules over simplicial rings some statement taken from John Francis' blog comment
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 10th 2010
- (edited Jan 10th 2010)
added an example-section on G-sets as the basic example of the generalized notion of module in the sense of enriched category theory
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeJan 10th 2010
We should be careful -- these guys at many places say that the infty-stable categories agree with A-infinity and other approaches only over fields in characteristics zero. I am not competent to judge, but I would be careful not to go back and forth freely.
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeJan 10th 2010
I think modules (some say algebras) over monads qualify as an important generalization in this entry. We also lack the treatment of modules over monoids in nonstrict monoidal categories, to include the coherences in the definition. I may do this, but if you wait for this it will take a while (tomorrow my boss is returning and we have a paper to finish these days).
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeJan 11th 2010
- (edited Jan 11th 2010)
Following Zoran's suggestion I added a paragraph on algebras over a monad
Then I typed more details of the proof that
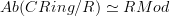 .
.Finally I rearranged the existing examples section: with the different notions being discussed, I thought it would be beter to have the examples collected in the subsections that disscuss the definition of which they are an example of.
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeJan 11th 2010
- (edited Jan 11th 2010)
There are analogues of this theorem (square zero extensions = abelian group objects in comma category) for Lie algebras and some other categories. See also the lecture notes (listed in the references) by Markl et al. One of the people who reintroduced expression module over monad instead of algebra over monad is Deligne in his influential article Categories Tannakiennes; for Grothendieck school this is a must: everything has to be done in relative point of view. The qcoh modules over a relative affine scheme are exactly modules over a monad in the qcoh of the base scheme which has some additional properties (including its own right adjoint).
As far as G-sets are concerned, one takes just the cartesian product with the group G and the modules over that monad are G-sets. This way one does not need enriched point of view, a usual monad will do.
I have one question about usage of [I,C] in codomain fibration and I in other categorical situations, e.g. in treatment of nonabelian cohomology. In one case I is directed on-groupoid category generated by one arrow 0 to 1; while in another I is a groupoid generated by arrows 0 to 1 and 1 to 0. So how can one justify that an interval is played by directed and sometimes by undirected category with two objects ?
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeAug 29th 2012
hereby I am moving an old discussion box from the entry module to here:
[begin forwarded discussion]
+– {: .query}
An earlier version of this entry led to the following discussion.
Eric: The wikipedia page distinguishes left R-modules as covariant functors and right R-modules as contravariant functors. Is that distinction important?
John: Yes, very — but I didn’t have the energy to get into that yet. For any ring R there’s a ring Rop in which xy is redefined to be yx. I defined a left R-module above; a right R-module is the same as a left Rop-module. Eventually we’ll have to discuss all this stuff, which becomes vastly more important when we start talking about bimodules. If we want to show off, we’ll do it all not just for rings, which are monoids in Ab, but more generally for monoids in any symmetric monoidal category. For any monoid M in a symmetric monoidal category we can define a new monoid Mop, and we can define left and right M-modules, and a right M-module is the same as a left Mop-module.
Sridhar: Given that left modules on rings are the covariant functors while right modules on rings are the contravariant functors, why does the above definition of a module on a monoid make the left modules the contravariant functors and the right modules the covariant functors? Is this actually the conflicting convention?
Toby: One problem is that this mixes with the conventions that one adopts for composition. What one person thinks is left multiplication, another will think is right multiplication. I would rather talk about left/right modules for monoids or rings, then talk about covariant/contravariant functors from categories or additive categories.
=–
[end forwarded discussion]
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeSep 1st 2012
I am working on brushing up and expanding the entry module, which has been quite a mess. So far I have
spelled out the full definition at Modules in a monoidal category
and then made the discussion of Module over a ring more systematically a special case of this.
Polished a bit more here and there. But this entry still deserves further editorial attention.
-
- CommentRowNumber10.
- CommentAuthorTodd_Trimble
- CommentTimeSep 1st 2012
- (edited Sep 1st 2012)
There is also a notion of module over an algebra over an operad[1], but I’m not sure how best to fit that in with the article. (I’d also like to think about the shape and size of the article.)
[1] There must be dozens of children’s songs like the one I’m thinking of: “there’s a flea on a fly / on the head of a frog / on a bump on a log / in a hole on the bottom of the sea”.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeSep 1st 2012
A link to module over an algebra over an operad is (well hidden) in the section Modules over higher and generalized algebras .
Yes, I agree, the entry still needs reworking. It’s too long, too much spread-out.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeSep 1st 2012
We have also model structure on modules over an algebra over an operad :-)
Not quite as long yet as the rhyme you quote. But getting close ;-)
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeSep 5th 2012
- (edited Sep 5th 2012)
At module I have added an Examples-section Examples of modules over a ring (just the basic examples). Also rearranged slightly to make the overall section structure cleaner.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeSep 11th 2012
added to the Idea-section of module a section Motivation for and role of of modules: generalized vector bundles with a bit of discussion of how to think of modules geoemtrically, and how that helps to explain their relevance.
-
- CommentRowNumber15.
- CommentAuthorzskoda
- CommentTimeOct 2nd 2012
- (edited Oct 2nd 2012)
I added a bit more on modules over a ring R as Ab-enriched functors, including the observation (quoted in MacLane) that, in this interpretation, the coend of the usual tensor product over integers is the tensor product over R.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeOct 14th 2012
added a section Abelian groups with G-action as modules over the group ring
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeOct 24th 2012
added a section Modules - As stabilized overcategories - Modules over a group.
-
- CommentRowNumber18.
- CommentAuthorTobyBartels
- CommentTimeJul 14th 2014
I emphasized where this article covers modules over an (enriched) category.
-
- CommentRowNumber19.
- CommentAuthorColin Tan
- CommentTimeJul 19th 2014
Is there discussion on the oo-categorial version of modules elsewhere in the Lab? Perhaps a concrete example is G CW-complex.
As a specific example, consider what a oo-module over the discrete group object ℤ/2 internal to ooGrpd ought to be (a homotopical version of real space. An ordinary module over the discrete group ℤ/2 is a set with an involution f (such that f∘f is the identity). Due to being unable to distinguish ℤ/2 from ΩℝP∞ under homotopy equivalences of group objects, a oo-module over the discrete group object ℤ/2 should be a oo-groupoid with a endomap f such that f∘f is homotopic to the identity. Has a general notion of oo-action by a group(oid) object internal to a Grothendieck (oo,1)-topos been stated elsewhere on the Lab?
A side remark: does KR theory make sense when the involution is only up to homotopy?
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJul 19th 2014
Sure, all higher categorical versions are always linked to from theitr 1-categorical counterpart entries.
Try module spectrum, (infinity,n)-module, (infinity,1)-module bundle, for instance.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJul 19th 2014
And for actions, see infinity-action. Naturally.
-
- CommentRowNumber22.
- CommentAuthoradeelkh
- CommentTimeJan 6th 2015
I extracted parts of the page into separate entries modules over a monoid and modules over an enriched category in order to be able to link to them from dg-module.
-
- CommentRowNumber23.
- CommentAuthorJ-B Vienney
- CommentTimeNov 24th 2022
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2023
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeAug 25th 2023
added pointer to:
- {#Lawvere92} William Lawvere, pp. 27 of: Introduction to Linear Categories and Applications, course lecture notes (1992) [pdf, Lawvere-LinearCategories.pdf:file]
(where R-modules are called R-linear spaces)
1 to 25 of 25