nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Discussion Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 11th 2010
- (edited Nov 7th 2012)
I edited the formatting of internal category a bit and added a link to internal infinity-groupoid
it looks like the first query box discussion there has been resolved. Maybe we can remove that box now?
-
- CommentRowNumber2.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 11th 2010
- (edited Jan 11th 2010)
internal-infinity groupoid in Top (nice topological spaces) suggest the notion of n-topological group. if is a toplogical space, then can be topologized, becoming a topological 1-groupoid. more interestingly, if is a topological group, should be a group object in toplogical 1-groupoids, i.e. a topological 2-group (I'd like to consider this example the prototypical topological 2-group, but I guess this is a matter of taste). by looking at as to a topological 2-group one obtains an obvious answer to the question Why is the universal cover of a (nice) topological group a topological group? namely, there is a natural topological groupoid map (here both groupoids are topologicla infinity-groupoids, the fact that the one on the left is a 0-groupoid and the one on the right a 1-groupoid tells us that morphisms are trivial from a certain point, but we do not look at i-groupoids and j-groupoids as objects in different categories from this point of view). taking the homotopy fiber (in groupoids) of over the identity object of one obtains a topological groupoid which is a 0-groupoid (since taking homotopy fiber decreases the "categorical height" by one). so this homotopy fiber is a topological group, and by construction it is the universal cover of .
This extends to higher "covers" of . let us denote by the universal cover. then should be topologized to give a group oject in topological 2-groupoids, and so a topological 3-group. taking homotopy fiber ends up in a natural structure of topological 2-group on the 2-connected cover of . and so on.
From this point of view it is natural to think to String(n) as a topological 3-group. this apparently contrasts both with the topological group point of view on String(n) and on the 2-Lie group point of view. however one is reconciled with the "correct" categorical height of String(n) if one thinks it is built as a homotopy fiber of the fourth delooping of , which is a topological 4-group. lowering down the categorical height of String(n) is then based on realizing as a topological 1-group. this way one trades the 2-group for a topological 1-group, and all levels in the construction of Spin(n) are lowered by one. and since the model for is a Lie 1-group, one can wonder (and actually succeed in finding) whether Sting(n) can be realized as a Lie 2-group. at the topological lever one can iterate the "lower the base step" trick, i.e. one can choose a model for which is a topological group, and so end up with String(n) as a topological 1-group.
maybe David Roberts could be interested in expanding this point of view. -
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeJan 11th 2010
I think that similar ideas for algebraic Galois group are used in Grothendieck's still unfullfilled ideas in his 1980s manuscripts and is in general known in Galois theory (covering spaces and higher Postnikov fibers have natural common generalizations in this context).
-
- CommentRowNumber4.
- CommentAuthorDavidRoberts
- CommentTimeJan 12th 2010
- (edited Jan 12th 2010)
Thankyou for taking an interest in the corner of the playground I frequent, Domenico. PI_1(X) can indeed be topologised, but composition is only continuous when X is locally nice - locally connected and semilocally simply connected. This pattern continues higher up, where increasingly stronger local conditions are needed. Note that to go all the way up to infinity-groupoids, one needs local contractibility. I will respond, but not right now. I only pause to remark that ultimately models of String should be smooth. One thing which I didn't pursue in my thesis, but was aware of, is that the 'universal' 2-covering space (not that I have proved it universal yet - only that it is 2-connected) is smooth when the base space is smooth. In this context one needs to be au fait with Frechet manifolds, sadly an area where I am lacking.
Edit: An easy way to see that the universal cover of a topological group X is topological is that the universal cover = the homotopy fibre of X --> Pi_1(X) at a point x = the source fibre of Pi_1(X) at x. This is a subgroup of the group of arrows, as Pi_1(X) is a strict 2-group as shown by Brown-Higgins in the 70s.
Edit2: The prototypical weak topological 2-group is the fundamental groupoid of a based loop space, subject to the above caveat. The strict case is pretty much as you say. -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 12th 2010
- (edited Jan 12th 2010)
not sure if this is relevant for what you have in mind, but taking path oo-groupoids can be made into a map from a lined oo-topos to itself. For instance taking a topological oo-groupoid
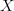 (might be just a topological space) to the topological oo-groupoid
(might be just a topological space) to the topological oo-groupoid 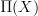 .
.Same for smooth oo-groupoids. For the smooth model of String, one can start with the Lie 2-algebra
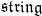 , then form the smooth space (sheaf)
, then form the smooth space (sheaf) 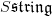 which is such that its plots
which is such that its plots 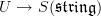 are precisely the flat
are precisely the flat 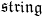 -valued differential forms on
-valued differential forms on 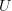 . Then one can form the smooth oo-groupoid
. Then one can form the smooth oo-groupoid 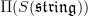 of that space. Finally, we can take from this simplicial sheaf degreewise the underlying concrete sheaf (=diffeological space) to get the smooth oo-groupoid
of that space. Finally, we can take from this simplicial sheaf degreewise the underlying concrete sheaf (=diffeological space) to get the smooth oo-groupoid 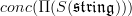 . The claim is that that's a smooth version of
. The claim is that that's a smooth version of 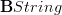 .
.This is discussed in some detail (though with slightly more antiquated tools than I have now) in section 5.2.3 here.
Concerning the categorical degree, I feel like remarking that it's only the homotopy groups (of an infinity-stack) that have intrinsic meaning, not the degrees of a truncated model.
Fur instance the goup
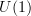 looks like, well, a group, but it is equivalent to the 2-group that comes from the crossed module
looks like, well, a group, but it is equivalent to the 2-group that comes from the crossed module ![\mathbb{R}//\mathbb{Z} = [\mathbb{Z} \hookrightarrow \mathbb{R}] \mathbb{R}//\mathbb{Z} = [\mathbb{Z} \hookrightarrow \mathbb{R}]](/extensions/vLaTeX/cache/latex_585a438ef55fbbd9d8c043a40fe16407.png) .
.Similarly, the String 2-group is a
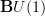 -central extension of an ordinary group
-central extension of an ordinary group 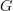 , hence a 2-group extension, but this is equivalent to a
, hence a 2-group extension, but this is equivalent to a 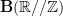 -central extension, which looks like a 3-group extension, but is really equivalent to the original 2-group extension.
-central extension, which looks like a 3-group extension, but is really equivalent to the original 2-group extension. -
- CommentRowNumber6.
- CommentAuthorAndrew Stacey
- CommentTimeJan 12th 2010
@David: you wrote
In this context one needs to be au fait with Frechet manifolds, sadly an area where I am lacking.
I have a little facility with Frechet manifolds. Is there something here that I could help with?
-
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeJan 12th 2010
Aha, he fell for my cunning plan! :)
But seriously...
I have proofs in chapter 5 of my thesis establishing Pi_2(X) as a topological bigroupoid for a locally well-behaved space X. I don't think it is too hard, given a fin. dim. manifold, to get the smooth (Frechet) structure on the _spaces_ involved in Pi_2, the trick is to show all the various structure maps (compositions, associator, unitor and unit/counit) are smooth. This is something I'm serious about doing, but I only have my spare time in which to do it, so it will be a slow process. -
- CommentRowNumber8.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 13th 2010
- (edited Jan 13th 2010)
<div> @David: <br/><br/><blockquote><br/>PI_1(X) can indeed be topologised, but composition is only continuous when X is locally nice - locally connected and semilocally simply connected.<br/></blockquote><br/><br/>This is nice: if I'm not wrong here these are exactly the conditions for X to have a universal cover; also I find it nice that one needs more and more local regularity as higher covers come into play. <br/><br/><blockquote><br/>An easy way to see that the universal cover of a topological group X is topological is that the universal cover = the homotopy fibre of X --> Pi_1(X) at a point x = the source fibre of Pi_1(X) at x. This is a subgroup of the group of arrows, as Pi_1(X) is a strict 2-group as shown by Brown-Higgins in the 70s.<br/></blockquote><br/><br/>That's exactly what I was trying to say. what i think is important to stress is that there is a subtle interplay here between topological and groupoidal aspects: from the topological perspective one ends up with an object which is clearly a simply connected cover and then has to show that this carries a natural group structure; from the groupoids point of view, the object one ends up with is clearly a group, but one now has to show that it is a simply conneced cover. And an incredible elegant way to prove both things at a time is to perform the two constructions independently, and to see that they produce the same object. here I think there should be some very general argument a priori telling me that the two constructions will lead to teh same object, but I'm still missing this argument.<br/><br/>@Urs:<br/><blockquote><br/>Concerning the categorical degree, I feel like remarking that it's only the homotopy groups (of an infinity-stack) that have intrinsic meaning, not the degrees of a truncated model.<br/></blockquote><br/><br/>edit: let me see if I correctly undersatnd this. if we start with the action groupoid of on what we are dealing with is not only a groupoid, but a groupal groupoid (since is a group and the -action is compatible with the group operation of ). so the 0-th truncation of this groupoid is a group. this 0-th truncation is evidently , so we should think of not as our basic object but rather as . right? </div> -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 14th 2010
well, it's better than that. The "groupal groupoid" (2-group) is equivalent, as a 2-group to the 2-group which is just the group .
The best way to see this is to notice that the obvious 2-functor of the corresponding delooping 2-groupoids is an equivalence: it is a k-surjective functor for all k. -
- CommentRowNumber10.
- CommentAuthorDavidRoberts
- CommentTimeJan 15th 2010
- (edited Jan 15th 2010)
As a small contribution, the discussion about U(1) is a special case of the (weak) equivalence of 2-groups \tilde G // pi_1(G) --> G for a topological group G admitting a universal cover \tilde G - where we forget the topology. If we try to do this in a 2-category of topological 2-groups, we need to use anafunctors for this to be an equivalence. -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJan 15th 2010
- (edited Jan 15th 2010)
Just a comment, probably no news to anyone, but just for the record:
to realize the equivalence as a homotopy equivalence (morphisms going back and forth, being weak inverses) one needs to find suitable ana-2-functors, inverting the evident morphism from one 2-groupoid to the other, but for just knowing that the two are equivalent it is sufficient to have that one morphism and checking that it is a weak equivalence.
This is true for topological infinity-groupoid realizations of the situation and even for Lie-infinity-groupoid realizations.
For that one may observe that the functor
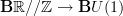 is k-surjective for all k on all stalks of Top or Diff: these are the germs of n-dimensional disks (as described by Dugger in the reference cited at topological infinity-groupoid.) So for
is k-surjective for all k on all stalks of Top or Diff: these are the germs of n-dimensional disks (as described by Dugger in the reference cited at topological infinity-groupoid.) So for 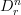 the standard n-disk of radius r, we form the groups of group-valued maps
the standard n-disk of radius r, we form the groups of group-valued maps 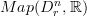 ,
, 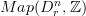 and
and 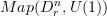 and then check that the functor of ordinary 2-groupoids
and then check that the functor of ordinary 2-groupoids 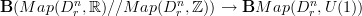 is k-surjective for all k for some r small enough. And it clearly is: on any disk, any U(1)-valued function (continuous or even smooth) may be lifted to an
is k-surjective for all k for some r small enough. And it clearly is: on any disk, any U(1)-valued function (continuous or even smooth) may be lifted to an 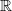 -valued function, and the nonuniquenss of the lifts are precisely given by
-valued function, and the nonuniquenss of the lifts are precisely given by 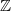 -valued functions on the disk.
-valued functions on the disk. -
- CommentRowNumber12.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 15th 2010
at first sight, the "equivalence of 2-groups" point of view confused me: if and are equivalent, why should I prefer ? but on second thought, I think a plausible perspective could be the following: both and are models for the same infinity-group; is a 1-connected model. one could go further and look for 2-connected models, 3-connected models.. of as an infinity-group, and it turns out that is such a model, since is infinity-connected. the same point of view would apply to other groups. e.g., I should not look at the string group as to something different from but rather as a 3-connected model of .
this could have some relevance in thinking to cohomology with coefficients in . namely, the "true object" is independent of the chosen model, but in carrying out explicit computations an highly connected model could be convenient (in nice situations, to compute one choses a fibrant replacement for ..). -
- CommentRowNumber13.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 15th 2010
- (edited Jan 15th 2010)
the above should be somehow relevant to nonabelian group cohomology. by the way, as it is stated at the beginning of that entry, nonabelian group cohomology largely discusses Schreier theory of nonabelian group extensions – but from the nPOV. this is a bit unsatisfactory: nonabelian group cohomology should be something more intrinsic form the nPOV, which is then seen to be equivalent to Schreier theory. namely, I find the use of AUT(K) something which works, but which is chosen in quite an arbitrary way. maybe it's worth creating a Schreier theory entry to discuss it (there's also a lot of material on this at group extension), so to make the other entrier related to Schreier theory lighter and more confined on their title subject (cleraly adding links to Schreier theory wherever needed). in particular nonabelian group cohomology could benefit from such a reorganization, since cohomology is one strong points of the nPOV slogan. my feeling is that nonabelian group cohomology could be rewritten making the fibration sequences the main tool, but even if this should tun out not to be incorrect, I'm not expert enough to attemp a reorganization of nonabelian group cohomology along these lines. -
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeJan 15th 2010
but on second thought, I think a plausible perspective could be
Yes, precisely: very different looking objects may all be equivalent to the same 2-group, (or the same oo-groupoid). The highest degree of nondegenerate cells is not an invariant under this. Instead, the main invariants are the intrinsically defined homotopy groups
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJan 15th 2010
I find the use of AUT(K) something which works, but which is chosen in quite an arbitrary way. maybe it's worth creating a Schreier theory entry to discuss it
Yes, I agree with all you say here. As far as I am concerned: I don't have the energy and time this particular project right now, though. Probably later sometime.
-
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeJan 15th 2010
- (edited Jan 15th 2010)
Schreier theory is included in group extension entry.
It is instructive the way Faro et al. pharse in their article, placing the role of AUT K via interpreting the Grothendieck construction. I will once write about it.
-
- CommentRowNumber17.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 16th 2010
- (edited Jan 16th 2010)
unfortunately, me too will be unable to seriously work on the lab for a couple of weeks. I'll just write something here for later use.. or immediate use if someone is interested in it and wants to pick it up :-)
in the nPOV approach to cohomology one basically defines only 0-th cohomology. cohomology in other degrees is then defined by shifting the second variable. a classical example is . this suggests that the natural setting for cohomology in different degrees is a stable (infinity,1)-category. for instance in nonabelian group cohomology with coefficients in the group , the natural object to work with seems to be the stabilization of . it would be interesting to compare this to Schreier theory. -
- CommentRowNumber18.
- CommentAuthorDavidRoberts
- CommentTimeJan 17th 2010
@Domenico, re 1-connected model
R//Z is not 1-connected _as a 2-group_, only its component spaces are (if we say that a disconnected space is 1-connected if its path-components are, which is a little bit of a fudge). This is still a desirable thing, though, as the topological complexity has been reduced (at the cost of introducing more algebraic structure). There are ways to define homotopy groups pi_n for topological groupoids (at least in print for n<3, and in my notes for all n) such that the map R//Z --> U(1) we have been discussing induces isomorphisms (this is contained in proposition 2.130 in my thesis, using U(1) = BZ). There is a bit of this in the work by Urs and Konrad Waldorf, but they are looking at the special case of a Cech groupoid. -
- CommentRowNumber19.
- CommentAuthorDavidRoberts
- CommentTimeJan 17th 2010
@Domenico, re nonabelian group cohomology
The point of nonabelian cohomology is to _not_ use stable theory, which is, at least in my view, a sort of minimal abelianisation of homotopy theory. But you are correct about using only 0-th cohomology. Actually I would say that there are, for n-group coefficients, two one would use: 0-th and 1-st. For example, take a 2-group G. We can then form the group H^0(X,G), and the pointed set H^1(X,BG). The first, for the case G = AUT(K) classifies K-bibundles, the second classifies K-bundle gerbes. This is in general, given an n-group, how much one can do - just H^0 and H^1. If H is an n-groupoid that can be delooped m times, we can form H^0, H^1,...,H^m by taking successive deloopings of the coefficients.
The most that Schreier theory can do (that I am aware of) for a group K is look at H^3, which we would now call cohomology with coefficients in BAUT(K). This was done in papers by Dedecker in the 50s. After this, I'm not sure what can be done. -
- CommentRowNumber20.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 17th 2010
<div> <blockquote>The point of nonabelian cohomology is to _not_ use stable theory</blockquote><br/><br/>so that's why it's called "nonabelian" or "unstable"! I should have known, but actually it was this remark above that really made me clear this fact, thanks!<br/><br/>still, I'd like to think of going from to as a suspension. in other words, when dealing with a cohomology with degrees I'd like to have two functors raising and lowering the degrees. in the stable theory these are looping and delooping, but one could have a nice theory in any case one has a nice shift. <br/><br/>this is somehow reminiscent of "old way" triangulated categories stuff. there teh shift functor is a basic datum; then in the stable infinity-category approach the shift is no more basic but it is recovered from homotopy pullbacks and pushforwards to the zero object. but we could still think of "unstable cohomology with degrees" as something coming from a shift functor which is not defined in terms of homotopy pullbacks/pushforwards to the zero object.<br/><br/>clearly, in order to have a nice and quite general theory, one would presumibly need not only the shift but also some good functorial behaviour. and then one could check that to indeed provides an example of this structure. </div> -
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJan 17th 2010
- (edited Jan 17th 2010)
There are ways to define homotopy groups
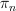 for topological groupoids
for topological groupoidsThere is, by the way, something even more general: the notion of homotopy group (of an infinity-stack)
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeJan 17th 2010
- (edited Jan 17th 2010)
a classical example is
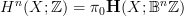 . this suggests that the natural setting for cohomology in different degrees is a stable
. this suggests that the natural setting for cohomology in different degrees is a stable 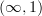 -category.
-category.It is true that only if the coefficient object has arbitrary delooping that the above definition of
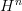 makes sense for all
makes sense for all  . But there is a priori no requirement that such a definition needs to make sense. For general nonabelian coefficients degree
. But there is a priori no requirement that such a definition needs to make sense. For general nonabelian coefficients degree  cohomology is defined only up to some finite
cohomology is defined only up to some finite  . This is a standard thing in the literature on nonabelian cohomology.
. This is a standard thing in the literature on nonabelian cohomology.But you can always form loops to go don do lower degrees.
-
- CommentRowNumber23.
- CommentAuthorDavidRoberts
- CommentTimeJan 17th 2010
@Domenico
The AUT construction is not a functor, as Aut is not an endofunctor on groups (Aside: this is why Giraud's original formulation of nonabelian cohomology from 1970 (or so) wasn't functorial in the 1-group K, but as we now know (following Debremecker, Aldrovandi-Noohi), it is functorial in the 2-group.) Certainly the autoequivalences of the delooping of an n-group form the objects of an (n+1)-group, but I don't know if the relation between the cohomologies with coefficients BK and Eq(BK) = AUT(K) has been studied for K a general n-group. -
- CommentRowNumber24.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 18th 2010
fine. so, till the right functorial setting is not clear, let us call a certain way of going from an n-group to an (n+1)-group just a "rule" R. for abelian groups this rule could be , whereas for an arbitrary group this could be (unpleasently, the two does not coincide on abelian groups, but this is classical and maybe unavoidable). so for each rule there is an higher cohomology with coefficients in a group : it is just cohomology with coefficient object . such a general nonsense accounts for cohomology with coefficients in an abelian group and for nonabelian group cohomology, but it is evidently something too general to be meaningful. so, the question is: what is reasonable to ask to R in order to have a good theory? clearly there could be classical cohomology theories where is not related to the n-th iteration of a rule R; it could be a good idea to try look at them from the nPOV to see what's really happening there. -
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeMar 8th 2012
Am hereby moving an old Discussion-section from internal category to here
[begin forwarded discussion]
Previous versions of this entry led to the following discussions
+–{: .query} I think things are mutliply inconsistent in this entry. I do not want to change as I do not know what the intentional notation to start with was. If p1;s=p2;t that mean that target is read at the left-hand side (composition as o, not as ;), while the diagrams before that suggest left to right composition. Then finally the diagram for groupoids has s both for source and inverse, and there is only for right inverse, and one should also check convention, once it is decided above.-Zoran
You're right; I think that I caught all of the inconsistencies now. Incidentally, one needs only inverses on one side (as long as all such inverses exist), although it's probably best to put both in the definition. (For groupoids, one also needs only identities on that same side too! This proof generalises.) —Toby =–
+–{: .query}
Question: I’ve looked at the definition of category in A for a while and still haven’t been able to absorb it. Could we walk through an explicit example, e.g. “This is exactly what C0 is, this is exactly what C1 is, this is exactly what s,t,i are, and this is how it relates to the more familiar context”? For example, an algebra is a monoid in Vect. I’ll try to step through it myself, but it will probably need some correcting. - Eric
Eric, one example to ponder is: how is an internal category in Grp the “same” as a crossed module? As a partial hint, try to convince yourself that given a internal category, part of whose data is (C1,C0,s,t), the group C1 of arrows can be expressed as a semidirect product with C0 acting on ker(s). The full details of this exercise may take some doing, but it might also be enjoyable; if you get stuck, you can look at Forrester-Barker. - Todd
Urs: I don’t know, but maybe Eric should first convince himself of what Todd may find too obvious: how the above definition of an internal category reproduces the ordinary one when one works internal to Set. Eric, is that clear? If not, let us know where you get stuck!
Tim: I have just had a go at 2-group and looked at the relationship between 2-groups and crossed modules in a little more detail, in the hope it will unbug the definition for those who have not yet ’groked’ it.
Eric: Oh thanks guys. I will try to understand how a small category is a category internal to Set first and then move on to category in Grp and the stuff Tim wrote. I’m sure this is all obvious, but don’t underestimate my ability to not understand the obvious :)
Eric: Ok. Duh. It is pretty obvious for Set EXCEPT for pullback. Pullbacks in Set are obvious, but what about other cases? Why is that important and what is an example where there are not pullbacks? In other words, is there an a example of something that is ALMOST a category in some other category except it doesn’t have pullbacks, so is not?
Tim: If I remember rightly the important case is when trying to work on ’smooth categories’, that is, general internal categories in a category of smooth manifolds. Unless you take care with the source and target maps, the pullback giving the space of composible pairs of arrows may not be a manifold. (I remember something like this being the case in Pradines work in the area.) The point is then that one works with internal categories with extra conditions on s and t to ensure the pullback is there when you need it.
Toby: Usually in the theory of Lie groupoids, they require s and t to be submersions, which guarantees that the pullback of any map along them exists. =–
[end forwarded discussion]
-
- CommentRowNumber26.
- CommentAuthorzskoda
- CommentTimeMay 20th 2012
- (edited May 20th 2012)
Reference
- Renato Betti, Formal theory of internal categories, Le Matematiche Vol. LI (1996) Supplemento 35-52 pdf
at internal category has a bogus pdf link which redirects to internal category! Is somebody having a correct pdf link ?
Urs 25, when you delete a discussion and archive it, then please leave the backlink to the archived version from the old place, otherwise is essentially lost. I done it this time (into references).
I have created a new entry locally internal category and listed it under related notions at internal category.
-
- CommentRowNumber27.
- CommentAuthorTim_Porter
- CommentTimeMay 20th 2012
- (edited May 20th 2012)
@Zoran I was not sure what you meant by the first sentence of locally internal category. I have amended it to mean what I think you meant but please check.
-
- CommentRowNumber28.
- CommentAuthorMike Shulman
- CommentTimeMay 21st 2012
I added a bit more.
-
- CommentRowNumber29.
- CommentAuthorzskoda
- CommentTimeMay 21st 2012
- (edited May 21st 2012)
Very nice, Mike !
On the other hand, why saying “in the sense of the appendix of (Johnstone)” at stack semantics, rather than more correctly attributing phrase “in the sense of Penon 1974”. Is there a slight difference ? (I did not look at Penon’s article yet; strangely I can find CR Acad Paris at the partly free gallica repository till 1973 and then again from 1979, but not for 1974-1978)
-
- CommentRowNumber30.
- CommentAuthorzskoda
- CommentTimeMay 21st 2012
I resolved the bogus pdf link which was asked about it 26 and will correct it at internal category in a minute:
- Renato Betti, Formal theory of internal categories, Le Matematiche Vol. LI (1996) Supplemento 35-52, pdf
-
- CommentRowNumber31.
- CommentAuthorMike Shulman
- CommentTimeMay 21st 2012
I didn’t write that phrase at stack semantics. Feel free to correct it if you know the correct reference.
-
- CommentRowNumber32.
- CommentAuthorTobyBartels
- CommentTimeMay 21st 2012
“in the sense of the appendix of (Johnstone)” was written by Ingo Blechschmidt.
-
- CommentRowNumber33.
- CommentAuthorIngoBlechschmidt
- CommentTimeMay 22nd 2012
zskoda: Sorry, that was indeed my mistake. It is fixed now. -
- CommentRowNumber34.
- CommentAuthorzskoda
- CommentTimeMay 22nd 2012
It is not a mistake, just more people together know more about the history :) and it is good when we agree (as often mathematicians do not agree on history).
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
I have brushed-up the entry internal category a little. Added the remark on cartesian closure discussed in another thread to a Properties-section
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeNov 8th 2013
- (edited Nov 8th 2013)
I just noticed how hard it is (or was) to find the crucial discussion at 2-topos – In terms of internal categories if all one does is search the nLab for “internal category”.
So I have now added a pointer to that at internal category by way of a brief paragraph a Properties – In a topos.
Should be expanded.
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeJun 13th 2018
added one more item to the list of examples:
- A groupoid internal to a category of presheaves is a presheaf of groupoids.
-
- CommentRowNumber38.
- CommentAuthorUrs
- CommentTimeMar 23rd 2021
added pointer to:
- Francis Borceux, Chapter 8 in Vol 1 Basic Category Theory of: Handbook of Categorical Algebra, Cambridge University Press (1994) (doi:10.1017/CBO9780511525858)
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeMar 23rd 2021
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeMar 23rd 2021
added publication data to:
- Jean Pradines, In Ehresmann’s footsteps: from Group Geometries to Groupoid Geometries, Banach Center Publications, vol. 76, Warsawa 2007, 87-157 (arXiv:0711.1608, doi:10.4064/bc76-0-5 )
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeMar 23rd 2021
added pointer to:
- Charles Ehresmann, Catégories structurées, Annales scientifiques de l’École Normale Supérieure, Série 3, Tome 80 (1963) no. 4, pp. 349-426 (numdam:ASENS_1963_3_80_4_349_0)
There are more articles by Ehresmann that would deserve to be cited here, but I am out of patience now and will leave it at that.
-
- CommentRowNumber42.
- CommentAuthorDavidRoberts
- CommentTimeMar 24th 2021
Added the real original reference:
- Charles Ehresmann, Catégories topologiques et categories différentiables Colloque de Géométrie différentielle globale, Bruxelles, C.B.R.M., (1959) pp.137-150
(Jean Pradines said in his talk at the New Spaces conference that the concept of Lie groupoid was already used, but not formally defined, by Ehresmann in earlier 1958 work on finite pseudogroups a la Cartan, but I haven’t yet found it. And possibly it is in Gattungen von lokalen Strukturen, but I wouldn’t be able to tell)
-
- CommentRowNumber43.
- CommentAuthorDavidRoberts
- CommentTimeMar 24th 2021
-
- CommentRowNumber44.
- CommentAuthorDavidRoberts
- CommentTimeMar 24th 2021
- (edited Mar 24th 2021)
I found Ehresmann’s 1958 paper in Compte Rendus on pseudogroups, and he uses the Lie groupoid of germs and certain Lie subgroupoids, but is really still just doing rather formal differential geometry, rather than thinking of Lie groupoids per se.
-
- CommentRowNumber45.
- CommentAuthorUrs
- CommentTimeMar 24th 2021
re #42 Thanks! That’s the way to go.
I am producing a standalone pdf of that article. In process…
I can have a look at “Gattungen…” but I haven’t gotten hold of that one yet, as it doesn’t seem to be in the oeuvres pdf
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeMar 24th 2021
So I uploaded a pdf copy of Ehresmann’s Catégories topologiques et categories différentiables.
Looking at it, I find it may be a little anachronistic to attribute the notion of internalization to this article: It defines topological and Lie categories by explicit description of the conditions, not by appeal to a general concept of internalization. The would-be ambient categories of TopologicalSpaces and of SmoothManifolds are not even being mentioned, are they? (I have only skimmed over it, I admit. If the actual notion of internalization is in there, let’s extract the page number and point to it.)
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeMar 24th 2021
It seems to be the actual notion of internal categories only appears later in
- Charles Ehresmann, Catégories structurées, Annales scientifiques de l’École Normale Supérieure, Série 3, Tome 80 (1963) no. 4, pp. 349-426 (numdam:ASENS_1963_3_80_4_349_0)
where it is probably Definition 3 in part II on p. 36.
(Not sure, though. I find reading this article is dizzying. Not the French, but the mathematical notation and terminology. So I don’t claim to have penetrated what it’s saying. If anyone has, let’s add specific pointers.)
-
- CommentRowNumber48.
- CommentAuthorDavidRoberts
- CommentTimeMar 24th 2021
Oh, I don’t claim the 1959 paper has any abstract notion of internalisation, but that’s not what the text was saying when I made the edit. But this paper gave what was they key motivation for the definitions of internal category and groupoid, rather than just a purely formal idea, and in categories without all pullbacks, to boot (a generality many other authors don’t consider).
Ehresmann is hard to read for many reasons, not least the non-Bourbaki-ized mathematical style (probably more influenced by Cartan) and the isolation from other category theorists leading to non-standard terminology.
-
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeMar 24th 2021
I adjusted the text after I suspected that your “real original reference” (#42) is not really about internal categories. It’s instead probably the original reference on topological categories and smooth categories , and I did copy it to there.
So possibly the first mentioning of internalization of categories is the reference given in #41. If you have the energy, you might sanity check whether we could quote Def. 3 on p. 63 there as the original definition (as suggested in #47).
-
- CommentRowNumber50.
- CommentAuthorDavidRoberts
- CommentTimeMar 24th 2021
I was looking at it, but I’ll have to come back. It seems that either Ehresmann is defining something only equivalent to what we would call an internal category, like maybe an externalisation, or else he’s only working in a concrete setting, since the definition of internal groupoid, for instance, just says that some data is a (plain!) groupoid, on top of having a structured category.
-
- CommentRowNumber51.
- CommentAuthorUrs
- CommentTimeMar 24th 2021
- (edited Mar 24th 2021)
Okay, thanks.
It seems then my impression (here) is correct that the credit for understanding and articulating the concept of internalization goes to Eckmann-Hilton 1961.
Oh the mysterious ways of attribution. This could well have been “Eckmann-Hilton theory”, but instead their names are hardly mentioned at all in this context, outside of their one eponymous example (of many they gave), and all authors use their term “group object” as if it was always called that way, since the beginning of time.
-
- CommentRowNumber52.
- CommentAuthorDavidRoberts
- CommentTimeMar 25th 2021
- (edited Mar 25th 2021)
This could well have been “Eckmann-Hilton theory”
to be honest, that’s a terrible way to name something. Giving people credit is not the same as using their names as the name of a thing. Imagine if we had “Eilenberg–Mac Lane theory” instead of “category theory”…
Maybe it’s a citation culture difference. Bénabou once tried publicly shaming me because my anafunctor paper had so many citations, whereas his bicategory paper had so few. Not to mention the whole issue of there not being category theory journals for so long that results were transmitted at meetings and conferences, and sometimes published in Springer’s LNM.
-
- CommentRowNumber53.
- CommentAuthorUrs
- CommentTimeMar 25th 2021
Hi David, don’t let yourself be distracted that easily. I was hoping you would come back with a closer reading of Ehresmann, as promised in #50. We are still looking for where in his writings we can first recognize the notion of internalization. I count on you.
-
- CommentRowNumber54.
- CommentAuthorDavidRoberts
- CommentTimeMar 25th 2021
Yeah, sorry :-). I’m going to have to ask on the categories mailing list, I think, or else take some more time to digest.
-
- CommentRowNumber55.
- CommentAuthorUrs
- CommentTimeMar 25th 2021
- (edited Mar 25th 2021)
Okay. If you do ask on the mailing list, please make clear that we are looking for the notion of internalization as such, not just for some construction that we can recognize, after the fact, as equivalent to an internalized structure.
-
- CommentRowNumber56.
- CommentAuthorUrs
- CommentTimeMar 25th 2021
moved a section “Internal vs. enriched categories” from internalization to here
-
- CommentRowNumber57.
- CommentAuthorDavid_Corfield
- CommentTimeMar 25th 2021
- (edited Mar 25th 2021)
The import from internalization needed some adjustment for its new home.
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeMar 25th 2021
All right, thanks. And maybe we should have the corresponding comment and cross-link also at enriched category. (Can’t edit myself right now.)
-
- CommentRowNumber59.
- CommentAuthorDavid_Corfield
- CommentTimeMar 25th 2021
We already have this section at enriched category. There are a lot of ideas there. Maybe even we could have a page on enrichment/internalization comparisons, and then link from each side. But that’s beyond my skills to synthesize.
-
- CommentRowNumber60.
- CommentAuthorDmitri Pavlov
- CommentTimeMar 25th 2021
Bénabou once tried publicly shaming me because my anafunctor paper had so many citations, whereas his bicategory paper had so few.
This is weird, since
16 citations: Roberts, David Michael Internal categories, anafunctors and localisations. Theory Appl. Categ. 26 (2012), No.29, 788–829. (Reviewer: Enrico Vitale) 18D05 (18F10 22A22)
336 Citations: Bénabou, Jean Introduction to bicategories. 1967 Reports of the Midwest Category Seminar pp. 1–77 Springer, Berlin (Reviewer: J. R. Isbell) 18.10
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeMar 25th 2021
- (edited Mar 25th 2021)
Clearly he meant items listed in the article’s bibliography, not citations to/of the article.
I guess it refers to the idea that the less you cite the more of a bigshot you must be.
-
- CommentRowNumber62.
- CommentAuthorAlec Rhea
- CommentTimeMar 25th 2021
-
- CommentRowNumber63.
- CommentAuthorDavidRoberts
- CommentTimeMar 25th 2021
@Dmitri,
Urs has it. Apparently it meant my ideas must have been less original (though that’s a shallow reading of bibliographic entries). But this is, as Urs pointed out, off the thread :-)
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeMar 26th 2021
It is somewhat on-topic in that it illustrates which social mechanisms are behind the desaster we have been struggling with above, of a whole field citing so unprofessionally as to forget the origin even of its most basic notions (here: internalization in general, which we discovered is due to Eckmann-Hilton, who are never credited for it, their peers possibly fearing to compromise their own originality if they did; and internal categories in particular, where tradition decided to attribute it to the article Catégories structurées which, however, on actual inspection, is at best a big mess).
I’m still interested in finding, and recording here, which reference first articulated the notion of internal categories, clearly.
Proper citation and attribution is part of professional academia. Not citing your precursors is not a sign of originality but of fraudulency.
-
- CommentRowNumber65.
- CommentAuthorDavid_Corfield
- CommentTimeMar 26th 2021
I’ve added in a link to the parallel treatment of the internalization/enrichment comparison at enriched category.
-
- CommentRowNumber66.
- CommentAuthorUrs
- CommentTimeJun 18th 2021
- (edited Jun 18th 2021)
At long last, we have found the origin of the definition of internal categories (thanks to Dmitri here!):
- Alexander Grothendieck, p. 106 (9 of 21) of: Techniques de construction et théorèmes d’existence en géométrie algébrique III: préschémas quotients, Séminaire Bourbaki: années 1960/61, exposés 205-222, Séminaire Bourbaki, no. 6 (1961), Exposé no. 212, (numdam:SB_1960-1961__6__99_0, pdf)
I have added that reference now, together with the precursor
- Alexander Grothendieck, p. 340 (3 of 23) in: Technique de descente et théorèmes d’existence en géométrie algébriques. II: Le théorème d’existence en théorie formelle des modules, Séminaire Bourbaki : années 1958/59 - 1959/60, exposés 169-204, Séminaire Bourbaki, no. 5 (1960), Exposé no. 195 (numdam:SB_1958-1960__5__369_0, pdf)
where the general definition of internalization is given.
So then, to the reference of Ehresmann’s “Catégories structurées” – which most authors cite as the origin of internal cateories – I have added the comment that
the definition is not actually contained in there, certainly not in its simple and widely understood form due to Grothendieck61.
-
- CommentRowNumber67.
- CommentAuthorDavidRoberts
- CommentTimeJun 19th 2021
And, interesting to note, that second, precursor, reference also has the Yoneda embedding, and the fact it preserves finite products!
-
- CommentRowNumber68.
- CommentAuthorDELETED_USER_2018
- CommentTimeJun 20th 2021
- (edited Apr 11th 2023)
[deleted]
-
- CommentRowNumber69.
- CommentAuthorDavidRoberts
- CommentTimeJun 20th 2021
Absolutely!
-
- CommentRowNumber70.
- CommentAuthorUrs
- CommentTimeJun 20th 2021
- (edited Jun 20th 2021)
-
- CommentRowNumber71.
- CommentAuthorDELETED_USER_2018
- CommentTimeJun 20th 2021
- (edited Apr 11th 2023)
[deleted]
-
- CommentRowNumber72.
- CommentAuthorUrs
- CommentTimeJun 20th 2021
- (edited Jun 20th 2021)
Thanks. But checking out the web version on my system, it appears broken: Most of the pages I see there appear empty except for a section headline, and those that are not empty break off in the middle of a sentence after a few lines. (using Firefox 89.0.1 (64-bit) on Windows 10)
-
- CommentRowNumber73.
- CommentAuthorDELETED_USER_2018
- CommentTimeJun 20th 2021
- (edited Apr 11th 2023)
[deleted]
-
- CommentRowNumber74.
- CommentAuthorUrs
- CommentTimeJun 20th 2021
Oh, I see. Great.
-
- CommentRowNumber75.
- CommentAuthorUrs
- CommentTimeAug 28th 2021
added pointer to:
- Peter Johnstone, Chapter 2 of: Topos theory, London Math. Soc. Monographs 10, Acad. Press 1977, xxiii+367 pp. (Available as Dover Reprint, Mineola 2014)
-
- CommentRowNumber76.
- CommentAuthorUrs
- CommentTimeAug 28th 2021
added pointer to:
- Enrico Ghiorzi, Complete internal categories (arXiv:2004.08741)
-
- CommentRowNumber77.
- CommentAuthorjuliang
- CommentTimeJul 5th 2022
- (edited Jul 5th 2022)
I think the s and t in the 2nd-5th pullback diagrams in the Internal categories section are inconsistent with those in the first pullback diagram and the laws specifying the source and target of composite morphisms; the earlier diagrams have p1 being the first of the morphisms and p2 being the second in the composition (so s∘c=s∘p1 for example), whereas the 2nd-5th pullback diagrams seem to have them the other way round. But I may be wrong, so I am hesitant about making this edit.
-
- CommentRowNumber78.
- CommentAuthorjuliang
- CommentTimeJul 5th 2022
On further thought, I’m pretty sure I’m right so I’ll make the changes. Feel free to undo them if I’m wrong!
-
- CommentRowNumber79.
- CommentAuthornLab edit announcer
- CommentTimeJul 5th 2022
-
- CommentRowNumber80.
- CommentAuthorvarkor
- CommentTimeOct 4th 2022
-
- CommentRowNumber81.
- CommentAuthorvarkor
- CommentTimeOct 4th 2022
The definition of internal category is due to Grothendieck. However, what’s the earliest reference for internal functors, natural transformations, and profunctors?
-
- CommentRowNumber82.
- CommentAuthorUrs
- CommentTimeOct 4th 2022
For what it’s worth, Johnstone’s “Topos theory” (1977) considers internal functors in section 2.1 and internal profunctors in section 2.4. That seems to be the earliest mentioning of these concepts among the references already collected in the entry (here), though I have no idea if there is an earlier one.
-
- CommentRowNumber83.
- CommentAuthorvarkor
- CommentTimeOct 4th 2022
Internal profunctors and 2-cells between them are already present in §5.1 of Bénabou’s Les distributeurs (1973), which must be the earliest definition for those. I don’t see a definition of internal functor or natural transformation there, though I would imagine it to be known earlier.
-
- CommentRowNumber84.
- CommentAuthorUrs
- CommentTimeOct 4th 2022
- (edited Oct 4th 2022)
added pointer to
- Jean Bénabou, §5.1 of: Les distributeurs, Université Catholique de Louvain, Institut de Mathématique Pure et Appliquée, rapport 33 (1973) [pdf]
for the definition of internal profunctors (to readers who already know all about internal categories?).
-
- CommentRowNumber85.
- CommentAuthorvarkor
- CommentTimeOct 4th 2022
We have a page for internal profunctor, but it would seem reasonable to me to collapse that page into the internal category entry. There doesn’t seem to be an advantage to having two different pages. Would anyone object if I made this change?
-
- CommentRowNumber86.
- CommentAuthorMike Shulman
- CommentTimeOct 9th 2022
Well, I think there may be many places where someone would want to link directly to internal profunctor. It’s a different concept, so why not have a different page for it? The page internal category is already quite long.
-
- CommentRowNumber87.
- CommentAuthorUrs
- CommentTimeJan 22nd 2023
added pointer to:
- Bart Jacobs, Chapter 7 in: Categorical Logic and Type Theory, Studies in Logic and the Foundations of Mathematics 141, Elsevier (1998) [ISBN:978-0-444-50170-7, pdf]
-
- CommentRowNumber88.
- CommentAuthorUrs
- CommentTimeMay 20th 2023
added pointer to:
- Saunders MacLane, §XII.1 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (second ed. 1997) [doi:10.1007/978-1-4757-4721-8]
-
- CommentRowNumber89.
- CommentAuthorUrs
- CommentTimeSep 16th 2023
added pointer to:
- Jean Bénabou, §5.4.3 in: Introduction to Bicategories, Lecture Notes in Mathematics 47 Springer (1967) 1-77 [doi:10.1007/BFb0074299]
-
- CommentRowNumber90.
- CommentAuthorUrs
- CommentTimeNov 8th 2023
added pointer to:
Marta Bunge, Robert Paré, Stacks and equivalence of indexed categories, Cahiers de Top. et Géom. Diff. Catég 20 4 (1979) 373-399 [numdam:CTGDC_1979__20_4_373_0]
Marta Bunge, Stack completions and Morita equivalence for categories in a topos, Cahiers de Top. et Géom. Diff. Catég 20 4, (1979) 401-436 [numdam, MR558106]
André Joyal, Myles Tierney, Strong stacks and classifying spaces, in: Category Theory (Como, 1990), Lecture Notes in Mathematics 1488, Springer (1991) 213-236 [doi:10.1007/BFb0084222]
Tomas Everaert, Rudger W. Kieboom, Tim Van der Linden, Model structures for homotopy of internal categories, Theory and Applications of Categories, 15 3 (CT2004) 66-94 [tac:15-03]
-
- CommentRowNumber91.
- CommentAuthorvarkor
- CommentTimeDec 9th 2023
Moved content to enrichment versus internalisation.
-
- CommentRowNumber92.
- CommentAuthorvarkor
- CommentTimeOct 1st 2024
-
- CommentRowNumber93.
- CommentAuthorvarkor
- CommentTimeOct 1st 2024
1 to 93 of 93