nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 14th 2010
I wanted to add to rational homotopy theory a section that gives a summary overview of the two Lie theoretic approaches, Sullivan's and Quillen's, indicating the main ingredients and listing the relevant references, by collecting some of the information accumulated in the blog discussion.
But, due to my connection problem discused in another thread, even after trying repeatedly for about 45 minutes, the nLab software still regards me as a spammer and won't let me edit the entry.
I'll try again tomorrow. Meanwhile, in case a good soul here can help me out, I post the text that I wanted to add to the entry in the next message. It's supposed to go right after the section ""Rational homotopy type".
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 14th 2010
## Lie theoretic models for rational homotopy types
There are two main approaches in rational homotopy theory for encoding rational homotopy
types in terms of Lie theoretic data:
1. In the **Sullivan approach** a 1-connected rational space,
in its incarnation as a simplicial set,
is turned into something like a piecewise smooth space by realizing
each abstract $n$-simplex by the standard $n$-simplex in $\mathbb{R}^n$; and
then a dg-algebra of differential forms on this piecewise smooth space
is formed by taking on each simplex the dg-algebra of ordinary rational polynomial
forms and gluing these dg-algebras all together.
This goes back to
* Dennis Sullivan, _Infinitesimal computations in topology_ .
1. In the **Quillen approach** the loop space of the rational space/simplicial set is formed
and its H-space structure strictified to a simplicial group, of which
then a dg-Lie algebra (a strict L-infinity-algebra) is formed by
mimicking the construction of the Lie algebra of a Lie group from the
primitive elements of its completed group ring: the group ring of the
simplicial group here is a simplicial ring, whose degreewise primitive elements
hence yield a simplicial Lie algebra. The Moore complex functor maps this
to the dg-Lie algebra functor that models the rational homotopy type in the
Quillen approach.
This goes back to
* Dan Quillen, _Rational homotopy theory_, The Annals of Mathematics,
Second Series, Vol. 90, No. 2 (Sep., 1969), pp. 205-295
([JSTOR](http://www.jstor.org/stable/1970725))
The connection between these two appoaches is discussed in
* Martin Majewski, _Rational homotopy models and uniqueness_ , AMS Memoir (2000):
the Sullivan dg-algebra of forms is dual to an L-infinity algebra
and may be strictified to a dg-Lie algebra, and this is equivalent to
the dg-Lie algebra obtained from Quillen's construction. -
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeJan 14th 2010
- (edited Jan 14th 2010)
OK, I've posted that.
I made the header
###instead of##to fit in with the headers that already existed.I also indented the references inside the bullet points.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 14th 2010
Thanks, Toby! -
- CommentRowNumber5.
- CommentAuthorTim_Porter
- CommentTimeFeb 28th 2010
@ Urs Some of the code and text from differential forms on simplices might be useful for some of your recent rational homotopy entries (saving you time).
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeFeb 28th 2010
- (edited Feb 28th 2010)
right, I am working on rational homotopy theory in an (infinity,1)-topos
I may need to talk about differential forms on simplices in a while, then I shall link to this entry, yes.
for the moment, it is noteworthy what one can say without using forms on simplices. I think if one goes through this story (i.e. in Toen's article) one finds that replacing a copy of
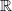assigned to a simplex with the quasi-isomorphic dg-algebra of forms on that simplex before taking the limit over all simplices serves to make the (quasi-isomorphic) result land in commutative dg-algebras, instead of in non-commutative ones. So its something like a choice of cofibrant replacement more than an intrinsic operation. -
- CommentRowNumber7.
- CommentAuthorTim_Porter
- CommentTimeMar 1st 2010
That is what I would expect, in as much as I have looked at Toen's stuff. Karoubi wrote some articles on a non-commutative analogue of this, I seem to remember.
The relevant list of publications of Karoubi is at http://people.math.jussieu.fr/~karoubi/Topologie.algebrique.html
1 to 7 of 7