Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: geometric theory

Bottom of Page

1 to 40 of 40

  1.  
    • CommentRowNumber1.
    • CommentAuthorMike Shulman
    • CommentTimeJan 14th 2010

    Added a description of several different approaches to geometric theory.

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeJan 14th 2010
    • (edited Jan 14th 2010)
    is there a good example of a geometric theory to keep in mind? I have looked at your entry, but I am still lacking a feeling for what geometric theories are like. Some motivating examples would maybe help me.
    • CommentRowNumber3.
    • CommentAuthorTobyBartels
    • CommentTimeJan 14th 2010

    First of all, every cartesian theory, regular theory, or even coherent theory is a geometric theory. Of course, we don't have those articles yet, but perhaps Mike is planning to write them. In any case, they certainly include all finitary algebraic theories, but also a lot more.

    A good example of a coherent theory that is not algebraic (in any of the usual senses, although it comes from algebra) is the theory of a local ring; a similar example is the theory of a discrete field.

    But to really answer your question, I need an example of a geometric theory that is not coherent. I actually don't know of a good example; it would involve some sort of infintary disjunction (indexed by an external set, like some sort of ground field or the set of all natural numbers, not by an internal object, since coherent theories can have that). Perhaps Mike does, or perhaps there is one in the Elephant.

    • CommentRowNumber4.
    • CommentAuthorTobyBartels
    • CommentTimeJan 14th 2010

    Looks like we do have a stub at coherent logic already.

    • CommentRowNumber5.
    • CommentAuthorMike Shulman
    • CommentTimeJan 14th 2010

    I didn't have immediate plans to write those other articles; geometric theories are in some sense the most important. One nice example of a (propositional) non-coherent geometric theory is the theory of a real number, whose classifying topos is the topos of sheaves on R. There are some other good ones in the Elephant, I'll look them up and add some examples to the page.

    • CommentRowNumber6.
    • CommentAuthorMike Shulman
    • CommentTimeJan 14th 2010

    I added some examples to geometric theory.

    • CommentRowNumber7.
    • CommentAuthorTobyBartels
    • CommentTimeJan 15th 2010

    I thought of another example and added it: the theory of a finite set. (Mike should probably check to make sure that there isn't a stupid mistake there, but it looks right to me.)

    • CommentRowNumber8.
    • CommentAuthorMike Shulman
    • CommentTimeJan 15th 2010

    I don't think you can take the disjunction of a set of sequents. The disjunctions have to happen inside the positive formulae on either side of the sequents.

    • CommentRowNumber9.
    • CommentAuthorTobyBartels
    • CommentTimeJan 15th 2010

    Dang, you're right! (And without loss of generality, the disjunctions take place on the right-hand side.) So there's my stupid mistake.

    But it would have been a nice example, wouldn't it?

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeJan 15th 2010
    • (edited Jan 15th 2010)

    Thanks for the large number of examples!

    I haven't really absorbed this, though. Maybe I don't really fully know what a "theory" is and what it even means for it to be preserved under geometric morphisms.

    I also don't know what "extensional essence" of a Grothendieck topos means.

    I know what a Lawvere theory is, some kind of category. Is the idea that I define a Lawvere theory in a topos T1 as a cateory internal to T1 and then ask if its image under a geometric morphisms 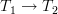T_1 \to T_2 takes it to an internal categeory that is still a Lawvere theory?

    If the answer is: "yes, sure, what did you think?" I'll add a remark making this explicit...

    • CommentRowNumber11.
    • CommentAuthorMike Shulman
    • CommentTimeJan 16th 2010

    Sorry, I mis-wrote. It's the topos that's the extensional essence of the theory, not vice versa. And it's not the theory that's preserved by geometric morphisms, only its models. The theory itself is defined independently of any topos (or, if you like, internal to the base topos, which is usually Set). Does that help?

    • CommentRowNumber12.
    • CommentAuthorMike Shulman
    • CommentTimeJan 16th 2010

    @Toby: On p815 of the Elephant is described a different sort of "theory of a finite set" which has one n-ary relation symbol 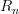R_n for each n, where 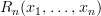R_n(x_1,\dots,x_n) is to be interpreted as "the elements 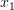x_1 through 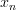x_n exhaust the set." Its models in Grothendieck topoi are the K-finite objects.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeJan 16th 2010
    • (edited Jan 16th 2010)

    So a theory is some category, a model is a (co)presheaf on it with special properties, and the question is whether these properties are preserved under functors on the (co)presheaf topos?

    • CommentRowNumber14.
    • CommentAuthorTobyBartels
    • CommentTimeJan 17th 2010
    • (edited Aug 16th 2010)

    I still think of a theory (not yet existing, but one of us should write something there) as usually understood in logic, that is as something specified syntactically. If a theory of some kind (of some ‘doctrine’, roughly speaking) can be characterised by a category, then so much the better, but I don’t think of that as what the theory is.

    In fact, I doubt that every useful kind of theory can be described as a category (consider the theory of a category, for example), although I have hopes that they might all be describable as ∞\infty-categories. So ideally, the choice to view a theory as a syntactic concept or as a higher category should simply be a matter of taste and perpsective.

    Anyway, yes, if you specify a theory by a category, then (at least in the simplest situation) a model of the theory is a functor from that category to SetSet, possibly equipped with extra stuff/structure/property. However, you can also consider models in some other category; for example, a model in TopTop of the theory of groups is a topological group.

    • CommentRowNumber15.
    • CommentAuthorMike Shulman
    • CommentTimeJan 17th 2010

    @Toby: The theory of categories can be described as a category, namely the syntactic category of the theory of a category. It's not a Lawvere theory, since the theory of categories is not a finite-product theory, but rather is a lex category, since the theory of categories is "essentially algebraic." Internal categories in a lex category C are equivalent to lex functors into C from the syntactic category.

    I do also prefer to think about "theories" as being syntactically described, with the resulting syntactic category encapsulating the "extensional essence" of the theory (relative to a given doctrine). In particular, two theories with equivalent syntactic categories are "Morita equivalent" in the sense that they have the same models in all categories (in the relevant doctrine), but I would still not call them the same theory. The other point of view is valid too, though, and from that perspective you can say that a theory is a (small) category T in some doctrine, and a T-model in a category C (in the same doctrine) is a functor 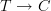T\to C (in that doctrine). In particular, Lawvere theories are the same as theories in the doctrine of finite products (the extra condition separating Lawvere theories, as usually defined, from arbitrary small categories with finite products, is just a "cofibrancy" condition that can safely be ignored if you allow your functors to preserve finite products non-strictly).

    I'm not sure if that's exactly what you meant by "(co)presheaf," Urs. I think of "presheaf" as usually meaning a functor with values in Set, whereas here the whole point is that the functors can take values in arbitrary categories (in the doctrine).

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeJan 17th 2010
    • (edited Jan 17th 2010)

    okay, so preservation of models under geometric morphisms is about whether a functor 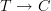T \to C composed with some functor 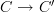C \to C' yields a functor 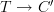T \to C' that still satisfies some conditions?

    • CommentRowNumber17.
    • CommentAuthorTobyBartels
    • CommentTimeJan 17th 2010

    @ Mike:

    But is that really the theory of categories? I would say that it is the theory of strict categories; in particular, it includes a notion of equality of objects. It is perhaps the closest approximation to the theory of categories that is itself a category, but it contains extraneous features in the resulting language and does not automatically recover the desired notion of when two categories are equivalent. One can only notice this if one has a previous, more logically oriented notion of what the theory of categories is, derived from practice.

    Technical note: An arbitrary (small) category with finite products corresponds to a typed finite-products theory (with smally many types), while a Lawvere theory as usually defined corresponds to an untyped finite-products theory. But that disctinction is also not terrible essential; the generalisation to simply typed theories is quite natural and easy to handle.

    • CommentRowNumber18.
    • CommentAuthorMike Shulman
    • CommentTimeJan 17th 2010

    @Urs: yes, that's one way to say it. In a sense, though that trivializes the idea, or incorporates it into the definition; the real meat being then in the correspondence between the syntactic presentation of theories and their syntactic categories.

    @Toby: To be completely precise, I would call it the theory of internal categories in the doctrine of lex categories. Some people might call it the theory of small categories; strict categories is reasonable too. I agree that this is not the same as the speak-no-evil approach that the two of us, at least, would prefer to regard as "the theory of categories," but I think saying without explanation that "the theory of categories is not a category" gives the wrong impression.

    Regarding typing, I presume that by "untyped" you mean what I would call "single-typed." And yes, I generally tend to gloss over the natural-and-easy generalization to multiple types, but maybe that is a bad habit.

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeJan 18th 2010

    okay. I created theory with the little that I understand about it now. Puny as it is, this bit of information is what I was lacking when reading geometric theory

    • CommentRowNumber20.
    • CommentAuthorUrs
    • CommentTimeJan 18th 2010

    By the way, it seems that elsewhere on the Lab Lawvere theories at least are not distinguished from their syntactic categories. The entry on Lawvere theory says that a Lawvere theory is a certain catgeory. In view of your comments above, maybe the wording should be made more precise?

    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeJan 18th 2010

    also, typically on the lab it says that a model is a functor to 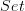Set. In order to understand the entry geometric theory one should probably say that in general a model is something in an arbitrary topos?

    • CommentRowNumber22.
    • CommentAuthorTobyBartels
    • CommentTimeJan 18th 2010
    • (edited Jan 18th 2010)

    A model is, by default, a functor to Set, much as a presheaf is, by default, a functor to Set. But in both cases, one can considers other targets if one wishes (topological models, ring-valued sheaves, etc). And some fields may even have a different default (although I don't know that any do for models).

    The term Lawvere theory generally does mean a category; it was Lawvere who first said that we can think of theories as categories rather than as linguistic constructs (with finite-products theories as the first example), and we honour him for his insight with this name.

    • CommentRowNumber23.
    • CommentAuthorUrs
    • CommentTimeJan 18th 2010
    • (edited Jan 18th 2010)

    A model is, by default, a functor to Set, much as a presheaf is, by default, a functor to Set.

    Fine, but so the reader of the entry on geometric theories should be alerted that here we consider explicitly models in arbitrary toposes and how they behave as we move geometrically between these.

    The term Lawvere theory generally does mean a category

    Okay with me, I just made that remark in the light of Mike's comment that

    ... that trivializes the idea, or incorporates it into the definition; the real meat being then in the correspondence between the syntactic presentation of theories and their syntactic categories.

    I am not the expert on this stuff. I am just giving you feedback on how I perceive the entry on geometric theory. When I first read it, it wasn't clear to me if the toposes in question were those where the models take values, or were the toposes of Set-valued presheaves in which the Set-valued models live. So that should be said explicitly in the entry.

    • CommentRowNumber24.
    • CommentAuthorMike Shulman
    • CommentTimeJan 18th 2010

    I made that comment because we were talking about theories in general, not specifically about Lawvere theories, and to me the default meaning of "theory" is syntactic, not a category. In other words, "Lawvere" is a red herring adjective. (-:

    I think it depends on your background whether a model is by default in Set. That's certainly true in model theory, but not so much in categorical logic. But clarification in any particular context is always a good idea.

    • CommentRowNumber25.
    • CommentAuthorUrs
    • CommentTimeJul 10th 2010

    I renamed at geometric theory the section that used to be titled “from logic to geometry” to In terms of sheaf topoi. Then I put a standout box around the statement that geometric theories are effectively identified with sheaf topoi.

    • CommentRowNumber26.
    • CommentAuthorJohn Baez
    • CommentTimeJul 13th 2010

    Mike wrote:

    In a sense, though that trivializes the idea, or incorporates it into the definition; the real meat being then in the correspondence between the syntactic presentation of theories and their syntactic categories.

    I got the impression from Jim Dolan that going from the “syntactic presentation” of a theory to the corresponding category was mainly a bunch of bureaucratic red tape, and that the really fun starts when we get past that stage and think of theories as being those categories. Sort of like how groups are more fun than group presentations, though of course those presentations are very useful. So, I’m a bit surprised that you seem to be taking more of the viewpoint of the traditional fuddy-duddy logician who likes nothing more than manipulating well-formed formulas according to purely syntactic rules - or at least contemplating such manipulations.

    • CommentRowNumber27.
    • CommentAuthorMike Shulman
    • CommentTimeJul 14th 2010

    I think that deserves a longer answer and a wider audience.

    • CommentRowNumber28.
    • CommentAuthorUrs
    • CommentTimeNov 8th 2011

    added a pointer to Barr’s theorem to geometric logic (in a new Properties-section)

    • CommentRowNumber29.
    • CommentAuthorNikolajK
    • CommentTimeJan 12th 2016
    • (edited Jan 12th 2016)

    The axioms for the existence of arrows/objects XX with a particular universal property (think: requirement that a category has a subobject classifier) always appear to go like “the category has an object, such that for every arrow from…”.

    I.e. ∃X.∀.…\exists X.\,\forall .\,\dots

    So are those theories then typically or always not geometrical theories?

  30. = included in definition of geometric theory.

    Steve Vickers

    diff, v37, current

  31. Tidying up presentation of theory of real numbers, to clarify difference between side conditions and sequents.

    Steve Vickers

    diff, v37, current

  32. Added example of flat diagrams, the most general theory of presheaf type.

    Steve Vickers

    diff, v39, current

    • CommentRowNumber33.
    • CommentAuthorThomas Holder
    • CommentTimeMay 14th 2020

    While providing some interconnections for theory of flat functors I saw that the nLab already had some material on this even in a nicer notation than the one I used in the other entry. Well, I set some pointers.

    diff, v40, current

    • CommentRowNumber34.
    • CommentAuthorThomas Holder
    • CommentTimeMay 19th 2020
    • (edited May 19th 2020)

    Added the empty and inconsistent theories as examples, as well as a link to an online version of the Reyes-Makkai monograph.

    diff, v42, current

    • CommentRowNumber35.
    • CommentAuthorThomas Holder
    • CommentTimeJun 14th 2020

    Since it is a good illustration of the expressiveness of infinitary disjunctions I’ve expanded the example of the natural numbers.

    diff, v43, current

    • CommentRowNumber36.
    • CommentAuthorMike Shulman
    • CommentTimeJun 14th 2020

    Tweaked the wording a bit. I think it would be helpful to give a link explaining the relevant notion of “complete theory”. Also, exactly what theory in FOL are we comparing it to? PA?

    diff, v45, current

    • CommentRowNumber37.
    • CommentAuthorThomas Holder
    • CommentTimeJun 14th 2020
    • (edited Jun 14th 2020)
    I was thinking of PA with the semantic equivalence between NNOs and models of PA in toposes in the background. I guess this might count as cheating though since it is not a fair competition on the syntax level. My main point here was mostly that the theory of standard sucessor algebra (homebrewed terminology I am not particularly happy with for its novelty but it seems to me to capture best what is in fact axiomaticized here) is indeed complete. Feel free to edit (away) the contrast with finitary FOL when you find it more irritating than helpful.

    Concerning your first point, the model theory of geometric logic in general is only sporadically covered on the nLab. If I find the time I'll add something in the near future, I guess definitions of quotient theory and expansion are also missing.
    • CommentRowNumber38.
    • CommentAuthorUrs
    • CommentTimeNov 24th 2021
    • (edited Nov 24th 2021)

    I have added pointer to this review:

    I came across this while looking for references that would make explicit the origin/motivation of the terminology “geometric logic” as indeed pertaining to geometry. On this point, Vickers’ text starts out with

    The historical roots of this idea must surely go back to Grothendieck’s dictum that “A topos is a generalized topological space”

    and then helpfully expands on the justification of the terminology. But do we know where the term actually originates and what the original source offered as motivation/explanation?

    diff, v49, current

  39. I replaced “all the same models in all Grothendieck topoi” by “categories of models in all Grothendieck topoi up to equivalence”, because that’s only what is true by the definition of classifying topoi!

    Vincent R.B. Blazy

    diff, v53, current

  40. I replaced “all the same models in all Grothendieck topoi” by “categories of models in all Grothendieck topoi up to equivalence”, because that’s only what is true by the definition of classifying topoi!

    Vincent R.B. Blazy

    diff, v53, current

1 to 40 of 40

  1.