nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: André Joyal's CatLab
Bottom of Page-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 19th 2010
- (edited Jan 19th 2010)
Dear André,
maybe we could use this thread here for conversation about issues related to your web, the CatLab. Notably you should drop us a note here whenever there is any question on wiki-related technical matters.
I saw that yesterday you started experimenting with the HomePage (joyalscatlab) by copy-and-pasting material from the nlab into it. This is good, you should get yourself acquainted with the inner workings of the wiki this way.
But seeing what you did, I thought I might be able to help a bit. Now, offering help is always dangerous, as the help might not in fact be desired. If the following does not suit you, just let me know and I'll "rollback" the status of the CatLab to exactly where you left it yesterday.
That said, I thought I'd indicate a bit how one could go about establishing the kind of wiki structure that it seems to me you intend to establish eventually.
Please have another look at your HomPage (joyalscatlab). You will see before the copy-and-pasted material that you had there, I have inserted a few lines. These are to indicate how one might make the HomePage something like a table of contents that guides the user to the deeper inner realms of the CatLab.
In a message in another thread you said that you are thinking of using the CatLat as a place to give an exposition of basic category theory using the natural model structure on Cat. Building on that comment I created an entry Homotopical Category Theory (joyalscatlab) on your lab. This currently contains nothing but a simple template into which one might fill further material. This is just meant as a suggestion. This entry can be renamed (for that click "edit" on the entry and then in the checkbox below the edit window click "change page name") or it can be entirely removed again.
All I want to indicate with this entry is how one might go about creating a web-structure of pages and links between them.
For doing these things the software provides the following technical tools. Some of them you probably already know, but I mention them anyway, just for the record:
creating a new page You create a new page on your web simply by creating a link to it: on any existing page you include somewhere in the text in double square brackets the name of the page to be created. Since the page does not exist yet, the link to it will appear in a grayish style, followed by a green question mark. Clicking on this question mark leads you to an edit box for a new page. Try it out, for instace, by clicking on one of the grayish links that I created at Homotopical Category Theory (joyalscatlab)
cross-web links There may be some material on the nLab that you feel you don't want to reproduce on the CatLab, but just want to point to. For that you create a link in double square brackets as usual, but precede the keyword inside it with "nLab:". For instance typing
[ [ nLab:category ] ]into an edit box on your web (without the spaces) will create a link on your web pointing to the entry "category" on the nLab.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 19th 2010
- (edited Jan 19th 2010)
Here is a problem that we ran into before:
the inclusion of the floating table of contents at HomePage (joyalscatlab) produces ill-formatted output.
Does anyone see how to fix this?
edit: now it works.
-
- CommentRowNumber3.
- CommentAuthorjoyal
- CommentTimeJan 19th 2010
Dear Urs,
I thank you very much for the CatLab and for your help.
There seems to be a bit of confusion about my plan for category theory.
I do not plan to develop the theory of homotopical categories in the CatLab, except possibly in relation with the theory of quasi-categories. I wish to use the natural model structure on Cat for developing certain basic aspects of category theory. I dont think that this is done anywhere, except in my personal notes. Incidently, I find it curious that the category theorists who claim (I dont really know who) that the natural model structure is "folk" have never used it in their work, except possibly very recently. I also would like to develop the theory of quasi-categories extensively in the CatLab. The theory exposed by Lurie in the Higher Topos Theory is very impressive, but badly done. The subject is not really that difficult.
I dont know exactly what the CatLab will be, and what will be its relation with the nLab. It could be a satellite of the nLab, or it may become more independant, only the future will tell. One may wonder why I am not writing in the nLab. Fundamentally, it is because I am old. I have developed over my lifetime a personal style which is now quite rigid, written in stone in my brain. I feel intolerant to certain ideas. Writing in the nLab demands flexibility, tolerance and times, all things I have scarcely. I intend to retire from the CatLab once my basic contribution is done, so that I wont be around to oblige peoples to think like myself! The nLab is open to all sort of novel ideas. All directions should be explored, because some of them may be fruithful. I have been wrong many times in my life in thinking that a direction was not worthy. -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 19th 2010
There seems to be a bit of confusion about my plan for category theory.
Sorry I must have misunderstood what you said, I took this from a recent message of yours here on the forum. But all I meant to provide was some more indication about how the coding of the pages work -- probably that was unnecessary. Please remove whatever of that doesn't fit your plans. I promise not to interfere again.
I find it curious that the category theorists who claim (I dont really know who) that the natural model structure is "folk" have never used it in their work
On the nLab the use of terminology was also influenced by the article A folk model structure on omega-Cat by Lafont, Metayer and Worytkiewicz. I don't really know of the origin of the term, and I take your point that "natural model structure" is more sensible. We should maybe change terminology accordingly on the nLab.
One may wonder why I am not writing in the nLab.
No worries, I think I understand your reasons.
The theory exposed by Lurie in the Higher Topos Theory is very impressive, but badly done. The subject is not really that difficult.
There should be a large demand for good expositions of quasi-category theory. As far as I am personally concerned: next term in Ieke Moerdijk's group in Utrecht we will run a kind of seminar on quasi-category theory, with an eye towards its generalization to quasi-operads (i.e. using dendroidal sets). I am in the process of preparing some seminar outline based on your Barcelona lecture notes and on Lurie's book. I'll be quite interested in whater of this topic you develop on the CatLab.
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeJan 19th 2010
Amusingly, I was just thinking earlier today that "folk model structure" should be changed. What about "categorical model structure"? Steve Lack comments on that in his recent preprint about the (whatever-it-is) model structure on Gray-cat. One reason I would prefer not "natural model structure" is that it suggests a connection with natural weak factorization systems, which is misleading (although the categorical model structure is "natural" in the latter precise sense).
-
- CommentRowNumber6.
- CommentAuthorjoyal
- CommentTimeJan 20th 2010
I would love to be able to quote a sentence by using a blue band as you do. Can you explain me how you do that?
Urs wrote:
[On the nLab the use of terminology was also influenced by the article A folk model structure on omega-Cat by Lafont, Metayer and Worytkiewicz. I don't really know of the origin of the term, and I take your point that "natural model structure" is more sensible. We should maybe change terminology accordingly on the nLab]
The "folk" model structure on omega-cat is not folk at all. Lafond told me that we was trying to respect a terminology adopted before (by who?) for the model structure on 2-categories
and for the "natural" model structure on Cat. I often call the model structure on 2-categories,
the "Lack model structure". Nobody can pretend seriously that the Lack model structure is folk.
The natural model structure on Cat was not folk, but it is easy to establish once you have the idea.
Maybe it could be called the "easy" model structure. But I would not want to say that the Lack model structure is the "easy" one. The "folk" terminology is completely wrong.
Michael wrote:
[Amusingly, I was just thinking earlier today that "folk model structure" should be changed. What about "categorical model structure"? Steve Lack comments on that in his recent preprint about the (whatever-it-is) model structure on Gray-cat. One reason I would prefer not "natural model structure" is that it suggests a connection with natural weak factorization systems, which is misleading (although the categorical model structure is "natural" in the latter precise sense).]
The "natural weak factorisation systems" look rather artificial to me. I never saw one (I do not mean to say that they are not interesting). I do not object strongly to calling them "natural", but I would prefer using another name. In any cases, I would hate to say that a Quillen model structure is "natural" because it is using some artificial "natural factorisation systems".
Mathematics is difficult and the terminology should help understanding the nature of ideas.
We should try to respect the meaning of the words in natural languages. I admit that this is sometime difficult. Let me tell a little story. Samuel Eilenberg once told me that when he wrote "Homological Algebra" with Henri Cartan, they putted a blank space instead of a word in their manuscript everywhere the terminology was uncertain. Because if you decide to use a temporary terminology, it sticks in your mind even if it is wrong. -
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeJan 20th 2010
I would love to be able to quote a sentence by using a blue band as you do. Can you explain me how you do that?
Make sure that the radio button labeled "Markdown" is selected below your comment box, and then put a ">" sign at the beginning of the line you want to quote.
The "folk" terminology is completely wrong.
No argument. I do believe that NWFS are, in fact, natural in the non-technical sense, though certainly more technically complicated than ordinary WFS, but certainly a more descriptive word like "algebraic" for them could be preferable. But I also think that "categorical model structure" for the model structures on Cat, 2Cat, etc. is more clear and descriptive than "natural model structure." Is there a reason you would prefer "natural model structure" over "categorical model structure"?
-
- CommentRowNumber8.
- CommentAuthorjoyal
- CommentTimeJan 20th 2010
Michael Shulman wrote:
But I also think that "categorical model structure" for the model structures on Cat, 2Cat, etc. is more clear and descriptive than "natural model structure." Is there a reason you would prefer "natural model structure" over "categorical model structure"?
I normally say that a notion is "categorical" if it is defined within category theory. The notion of Quillen model structure is categorical in this sense. I would say that every model structure is categorical.
The weak equivalences of the "blank" model structure on Cat are the equivalences of categories, a class of maps naturally found in category theory. The cofibrations and the fibrations of the model structure are natural in the same sense.
The naturality of the "blank" model structure on 2Cat also comes from the fact that its weak equivalences are the equivalences of 2-categories. Similarly for the "blank" model structure on omegaCat.
The Thomason model structure on Cat in not natural in category theory. I do not mean that it is against nature.
If the "blank" model structure is called "categorical", the Thomason model structure will become "non-categorical" by contrast , which is strange, since every model structure is categorical.
PS: Thanks for the blue band.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
What about "canonical model structure"? Canonical because categories do by their very nature already come with a notion of "weak" equivalence, and the blank-model structure is the one respecting that. While the Thomason model structure is not. So that is a non-canonical choice of model structure on Cat.
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeJan 20th 2010
Or ‘standard model structure’ in a similar vein?
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeJan 20th 2010
Urs, I haven't actually read what you're talking about, but it seems like that usage of 'canonical' would coincide with grothendieck's usage of it for topologies. It's the coarsest structure such that the 'usual nice properties' hold, if you will. However, I really don't know what you're talking about, so if what I said is blindingly stupid, you don't need to rub it in. -
- CommentRowNumber12.
- CommentAuthorjoyal
- CommentTimeJan 20th 2010
I think that the terms "canonical", "standard" and "natural" are quite good. The word canonical is often used for a structure which can be defined canonically. For example, every small category has a "canonical" Grothendieck topology. The "blank" model structure can be said to be canonical because it is using the "natural" class of equivalences in the given context. I must admits that the cofibrations and the fibrations are less obvious in the general cases, and there could be some variations. The word "standard" is good because it is up to the community to adopt a standard. However, a standard is often an arbitrary convention, like the meter standard. If the "blank" model structure is really natural, it should not be called "standard". What do you think? We may raise the problem at the categories list.
-
- CommentRowNumber13.
- CommentAuthorHarry Gindi
- CommentTimeJan 20th 2010
If the 'blank' model structure can be defined canonically, we might as well use canonical. It would be one of those great cases where a word means the same thing in different places. -
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
It is a pity that there is no formalization of what canonical means. It feels that just as category theory gave a formalization of what "natural" means, it should be able to give one for "canonical".
i remember John Baez once mentioned a formal definition of "canonical" by Jim Dolan. But I couldn't see how that proposal captured the right idea. I also forget what the proposal actually was, though.
-
- CommentRowNumber15.
- CommentAuthorHarry Gindi
- CommentTimeJan 20th 2010
Could you find that again? I've never seen it before. -
- CommentRowNumber16.
- CommentAuthorTobyBartels
- CommentTimeJan 20th 2010
Jim Dolan's definition of canonical transformation is … well, I'll just write it up at the Lab, shall I?
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Thanks, Toby!!
This reminds me: this kind of weakened natural transformation is precisely what Chris Schommer-Pries considers in one categorical degree higher in his work on extended TFTs with defects.
Search this entry for the word "unnatural" or "supernatural".
That might be of interest. Chris's observation in this context I hold in high regard: he characterizes (n-1)-dimensional TFTs with defects and boundaries(= 1-sided defects) as such weakened pseud-natural transformations between extended TFT n-functors on nCob.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
I added a reference to pdf-slides by Chris on what we would apparently now call "pseudo-canonical transformation" (i.e. the 2-categorical version) to canonical transformation
as far as I know the article corresponding to this is still in the making. I had tried to persuade Chris to make this a contribution for our book
-
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeJan 21st 2010
While I won't argue about the importance of transformations that are only natural with respect to isos (Chris' characterization is quite fascinating), I'm not immediately entranced by the prospect of appropriating for them yet another word which is widely used informally in mathematics to mean many different things, most of them having nothing to do with this concept. What about calling them something like "core-natural," since they are of course just a special case of natural transformations but only restricted to the core?
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
I second that. As I mentioned, I couldn't quite see why exactly this is called "canonical transformation". As Harry asks elsewhere: what's a motivating example?
Chris's example seems to be a very good one for the concept, but it also seems to be a very bad one as far as the term "canonical" is concerned, since canonical is one of the words that does not really come to mind when looking at Chris's setup.
-
- CommentRowNumber21.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
I always use the word canonical either to mean a minimal form of unique representation (canonical form of a rational number, etc.), or to mean "induced", but not necessarily by a universal property. -
- CommentRowNumber22.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
A canonical transformation is the general coherent notion of an operation from an object of one category to a morphism of another.
But I wrote it up simply because Urs was looking for it. But I don't mind saying that it may not be a very good term.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Toby, thanks, yes, I understand that, and I am grateful that you dug this information out so quickly. But Jim Dolan must have had something particular in mind when he invented that term. Do you happen to know if Jim Dolan was thinking of particular examples of "canonical transformations" that motivated the term for him?
-
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
I only know what's in the Usenet thread linked from the article.
-
- CommentRowNumber25.
- CommentAuthorjoyal
- CommentTimeJan 21st 2010
I claim that the "blank" model structure for omega-categories is very natural. Every model structure is determined by any two of its defining classes of maps: the cofibrations, the weak equivalences and the fibrations. It is easy to show that a model structure is also determined by its class of cofibrations together with its class of fibrant objects. Equivalently, it is determined by its class of acyclic fibrations together with its class of fibrant objects. There are many examples of model structures in which every object is fibrant, in which case the model structure is determined by its class of acyclic fibrations alone. Every omega-category is fibrant in the "blank" model structure. But a map between omega-categories is an acyclic fibration iff it is a trivial fibration as a map of globular sets . I call a map in a topos a trivial fibation if it has the right lifting properties with respect to every monomorphism.
The "blank" model structure for n-categories also depends entirely on its class of acyclic fibrations. A map of n-categories is an acyclic fibration iff it is an acyclic fibration as a map of omega-categories.
Of course, an explicit description of these maps can be given by using the notion of k-surjection introduced in the nLab. -
- CommentRowNumber26.
- CommentAuthorMike Shulman
- CommentTimeJan 21st 2010
That's a very compelling argument for the "naturalness" or "canonicity" of these model structures. The trivial fibrations of (n-)globular sets are also the maps that Makkai calls "very surjective" in his general logical framework of FOLDS. And in an "algebraic" model for higher categories it is very natural to expect all objects to be fibrant.
Of course, whatever we decide on here, different people will probably continue using various words like "categorical" or even (unfortunately) "folk." I think I would be okay with "natural model structure" if the majority likes that, but I would prefer "canonical." What you say points out that it is even "canonical" in a sense somewhat analogous to the canonical Grothendieck topology, namely, it is the model structure with the fewest possible weak equivalences, i.e. the most possible fibrant objects, given the particular class of acyclic fibrations (which are naturally defined, as you say, in any topos).
-
- CommentRowNumber27.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
I agree with Mike, and if this is a voting matter, I cast my vote for "canonical".
-
- CommentRowNumber28.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
I always liked ‘folk model structure’, which I know only from Urs's writings on the Lab, even though I never understood (or tried to understand) where it came from. So it's too bad that it doesn't really make sense.
If we were taking a vote, I'd go with ‘canonical’ (even though it has nothing to do with Jim's notion of that word, which I will leave to its own thread). But I'm not sure that my opnion should count.
-
- CommentRowNumber29.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
Zoran's one-line definition of canonical is better Dolan's definition anyway. Another pretty cool upshot: if our topos is a grothendieck topos, then it's also endowed with the canonical grothendieck topology by a theorem of Giraud.
-
- CommentRowNumber30.
- CommentAuthorjoyal
- CommentTimeJan 21st 2010
@:Shulman
Of course, whatever we decide on here, different people will probably continue using various words like "categorical" or even (unfortunately) "folk." I think I would be okay with "natural model structure" if the majority likes that, but I would prefer "canonical." What you say points out that it is even "canonical" in a sense somewhat analogous to the canonical Grothendieck topology, namely, it is the model structure with the fewest possible weak equivalences, i.e. the most possible fibrant objects, given the particular class of acyclic fibrations (which are naturally defined, as you say, in any topos).
Not a bad analogy:
Fibrant objects = sheaves
I agree.
-
- CommentRowNumber31.
- CommentAuthorjoyal
- CommentTimeJan 22nd 2010
Frankly, the diagrams designed in MathML are awful to watch. I am sure everybody hate them. It is a serious problem. Category theory cannot work without good diagrams. I am sure you have discussed this problem before. If it cannot be solved in MathML, we should use a trick, I dont know which, I am a computer illiterate. Is it possible to import a picture created elsewhere? Something like the picture of the Elves in the lab elf page?
-
- CommentRowNumber32.
- CommentAuthorTobyBartels
- CommentTimeJan 22nd 2010
- (edited Jan 22nd 2010)
Is it possible to import a picture created elsewhere?
There's a good tool for this at codecogs. After you type in the LaTeX (it also knows Xy), copy the HTML from the bottom and put that into your page. (Sometimes this improves with a little tweaking, but it should at least work as it is.)
There's also been a lot of discussion on even better systems for making diagrams (ideally something that can be easily edited and that produces SVG so that it looks good at all scales). There are some diagrams in the Lab that have been made that way, but there isn't a user-friendly system yet. (You can find these discussions on the forum in their own category.)
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
<p>Instructions for how to include diagrams are at</p> <p><a href="http://ncatlab.org/nlab/show/HowTo#diagrams">How to draw commutative diagrams and pictures</a></p> <p>I have just added to that section a description of how to use CodeCogs, with an example.</p> <p>NOTICE: the obvious way to do this is awkward and moreover does not work, as far as I can see, anymore on the Lab.</p> <p>But there is a better way, and it does work. I have explained this now at the above link, but here is the idea:</p> <p>you write code for an xypic-diagram as you would when typing it into a LaTex document.</p> <p>Then you do two things to it</p> <ul> <li><p>write it all in one single line, without any spaces anywhere</p></li> <li><p>replace all appearances of the symbol "&" by the symbols "%26"</p></li> </ul> <p>then take the string of symbols obtained this way, and include it on the nLab page where it should go as follows</p> <p><code></p> <p>[LEFTANGULARBRACKET]img src="http://latex.codecogs.com/gif.latex?YOUR-CODE-GOES-HERE" /[RIGHTANGULARBRACKET]</p> <p></code></p> <p>Sorry, I don't know who to better meta-typeset this here. See the above link for a more readable version.</p> <p>It is important to remove all the ampersands and replace then by "%26"s, because otherwise the HTML parser of the nLab will think this are commands it should try to interpret, instead of just passing it on as a URL to CodeCogs.</p> -
- CommentRowNumber34.
- CommentAuthorjoyal
- CommentTimeJan 23rd 2010
I thank you both for your explanations. I would love to understand them, but I am so dum with software technology that everything I can learn is by copying and modifying examples. I wonder if you could give me a few examples from the nLab, of diagrams made according to your recipe. Just tell me the name of the pages. The majority of my diagrams are very simple: a horizontal arrow between two objects, a commutative square with four arrows and four objects, a right-angled triangle with three arrows and three objects (there are actually four types of them according to the position of the right angle), a commutative square with a diagonal (there are two of them depending on the position of the diagonal). Of course, the arrows of the diagram may be decorated with a math symbol. I hope to be able to understand your explanations after examining a few examples. Thanks.
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
As I said, at the link I gave there is an example for copy-and-pasting.
(Unfortunately the nLab server is still down right this moment. We need to wait for either Andrew or Toby to get online and restart it).
But I'll send you the code by email. I can't post it here on the forum, because I don't know how to encode it here in a way that the forum software doesn't try to interpret it as commands.
-
- CommentRowNumber36.
- CommentAuthorHarry Gindi
- CommentTimeJan 23rd 2010
- (edited Jan 23rd 2010)
There's a way to make commutative diagrams entirely with the \matrix command like:<br /><br /><img src="/extensions/vLaTeX/cache/latex_efa5f19b737393f5e1064cbc9b2c18ce.png" title="\matrix{<br />X&\cong&S^{\Delta^1}_f &\to &Y^{\Delta^1}&\to& S^{\Delta^1}&<br />\cr &\searrow&\downarrow &Pb &\downarrow&Pb&\downarrow<br />\cr L_f&\cong &S_{t'} & \to &L'&\to& L & \to & S^{\{1\}} &<br />\cr &&\downarrow &Pb&\downarrow&Pb&\downarrow&Pb&\downarrow p<br />\cr &&\Delta^{0} & \to &(\Delta^1)^{\Delta^1} &\to& T^{\Delta^1} & \to & T^{\{1\}}<br />\cr &&&id&&(f)^{\Delta^1}&&d_1}" style="vertical-align:-20%;" class="tex" alt="\matrix{<br />X&\cong&S^{\Delta^1}_f &\to &Y^{\Delta^1}&\to& S^{\Delta^1}&<br />\cr &\searrow&\downarrow &Pb &\downarrow&Pb&\downarrow<br />\cr L_f&\cong &S_{t'} & \to &L'&\to& L & \to & S^{\{1\}} &<br />\cr &&\downarrow &Pb&\downarrow&Pb&\downarrow&Pb&\downarrow p<br />\cr &&\Delta^{0} & \to &(\Delta^1)^{\Delta^1} &\to& T^{\Delta^1} & \to & T^{\{1\}}<br />\cr &&&id&&(f)^{\Delta^1}&&d_1}" /><br /><br />The way you type this out here might not be exactly the same though. This is a pretty big commutative diagram I drew this way in a question on mathoverflow. I don't know if this works on nLAb, but it doesn't use xypic, so I think it should. -
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
Yes, something like this does work. Most of the diagrams on the nLab are coded like this currently.
But it is true that the output of this is not as nice as it should be. André was asking for a way that produces nice output. The use of CodeCogs pictures produces images that look exactly like standard LaTeX xypic diagrams.
This and three other ways of producing diagrams on the nLab are described at
How to draw commutative diagrams and pictures
(once the server comes up online again, that is...)
-
- CommentRowNumber38.
- CommentAuthorTobyBartels
- CommentTimeJan 23rd 2010
- (edited Jan 23rd 2010)
@ Harry
In the Lab, you have to use
\arrayinstead of\matrixand\\instead of\cr; then your method works. As Urs said, most of the diagrams are done that way currently.(PS: The server is back up.)
-
- CommentRowNumber39.
- CommentAuthorjoyal
- CommentTimeJan 23rd 2010
@:Urs
I followed your instructions in
http://ncatlab.org/nlab/show/HowTo#diagrams
and it worked very well!
http://ncatlab.org/joyalscatlab/show/Natural+transformations
But my diagram is not centered in the page. Could you please have it centered for me? (I best learn by an example).
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
- (edited Jan 23rd 2010)
Could you please have it centered for me?
Okay, I centered it, see Natural transformations (joyalscatlab)
you just need to enclose the "img"-tag by a "center"-tag. As you can see now from the source code of your page. Also at the Sandbox.
By the way: do you mean to title the page "Natural transformations" instead of "Natural transformation"?
In any case, you should know this: you can add to the very end of the source code of an entry , enclosed in double square brackets, the code "!redirects xyz" . That will make the entry appear whenever a link of name "xyz" is called for, even if the entrie's name is different.
You can see examples for this usage in almost every nLab page, for instance here. This might not look relevant now, but might become relevant when your CatLab grows.
-
- CommentRowNumber41.
- CommentAuthorHarry Gindi
- CommentTimeJan 24th 2010
- (edited Jan 24th 2010)
@Prof. Joyal (unless you'd prefer I call you André): On an unrelated note, do you have a suggestion for learning about quasicategories? I've tried to read Lurie's earlier sections which deal with a lot of the foundational results about SSet and its model structures, but his style regarding these topics is not really to my liking. I figured since you're here, you might have a suggestion (given the fact that most of the material in the sections I'm reading is either named by or for you.) More specifically, I'm talking about the chapter regarding left, right, and mid-fibrations, as well as their counterparts in the Joyal model structure.
I ask this because I was unable to find ref#44 in HTT, which is where many of the results are proven. However, in the preface, Lurie noted that you'd given him a copy of ref#44, and that it hadn't been published at the time. Is that still the case? If it is still unpublished, would it be presumptuous of me to ask for a copy?
The reference is:
Joyal, A. Theory of quasi-categories I. In preparation.
-
- CommentRowNumber42.
- CommentAuthorjoyal
- CommentTimeJan 25th 2010
@Gindi. I wonder if you could assist me in the CatLab? I will give you an access to my notes in exchange. You can write to me for discussing the details of the agreement, if you are interested. joyal.andre@uqam.ca.
-
- CommentRowNumber43.
- CommentAuthorjoyal
- CommentTimeJan 28th 2010
I have expanded the scope of the CatLab from category theory to categorical mathematics. I believe that category theory is best when interacting with other parts of mathematics. I do not mean to suggest that pure category theory is not good, because we must study the subject abstractly sometime. But I confess that I find it difficult to understand an abstract mathematical result when it is not illustrated by a few "concrete" examples (concrete=familiar). What we call "intuition" is most often rooted in the knowledge of a few examples. We are not fully aware of the difficulty of mathematics when we teach, because mathematics seem concrete to us. Our intuition is supported by examples that can be hidden to us.
-
- CommentRowNumber44.
- CommentAuthorjoyal
- CommentTimeJan 30th 2010
I keep changing my conception of the CatLab. It is now becoming more like Bourbaki. Maybe it should have a different name. I now think that it should contains a full description of categorical mathematics, including proofs. It will need an editorial board, because there will be important choices to make. If peoples dont like the choices, they will be free to create another CatLab with a different editorial board. The general public is best served when there is a variety of organisations competing to offer a service. Incidently, Howard Huges is one of my heros:
http://en.wikipedia.org/wiki/Hughes_H-4_Hercules
-
- CommentRowNumber45.
- CommentAuthorTobyBartels
- CommentTimeJan 30th 2010
If peoples dont like the choices, they will be free to create another CatLab with a different editorial board.
Will they be free to use the material produced before the split, particularly if they helped to contribute to the CatLab. (I mean if they leave because of a decision taken some time after the project is opened up.)
-
- CommentRowNumber46.
- CommentAuthorjoyal
- CommentTimeJan 30th 2010
@Toby. That's a good question. I dont have the answer. I do not know if it is technically possible (and desirable) to prevent peoples from copying. I guess that it would up to an editorial board to consider the problem. Personally, I dont worry about that. Stealing or copying may have a positive social role. I recall that during my trip in Australia in 1998, the phone company Telstra was refusing to give to the police the infomations it wanted for tracing back the stolen mobile phones. The mobile phones were quite expensive and many peoples, especially the youngs, could not afford one, except on the black market. The black market of stolen phones was a part of the marketing strategy of the company. If some peoples want to copy CatLab (or of the nLab) it will just help propagating the higher doctrine. It does not matter if they modify it because it may improve it sometimes, otherwise peoples will eventually want to return to the true faith.
-
- CommentRowNumber47.
- CommentAuthorTobyBartels
- CommentTimeJan 31st 2010
It's not technically possible to prevent people from copying, but it is extremely easy to make it illegal for people to copy. In fact, in most countries (including Canada, the U.S., the EU, etc), it is already technically illegal for people to copy the CatLab, by default.
For an informal lab, this is not a big deal (although we have discussed it on the Forum a few times). Urs is not likely to sue anybody, especially since any copiers will probably give him credit. (If they don't, the problem is plagiarism, not copyright infringement.) Even if he wanted to sue, this is very difficult when a document has been written by several people who have never worked out anything regarding copyright ownership.
But if you have an editorial board, then that is a single incorporated body of people who exercises control over all of the content, which makes it easier for them to sue if they were so inclined. And people on boards sometimes worry about their fiduciary duty, which makes them more likely to try if they think that the project can get money (or prestige, etc) out of it.
However, since you seem so eager to allow people to copy, I think that things will be fine. I just wanted to check.
-
- CommentRowNumber48.
- CommentAuthorHarry Gindi
- CommentTimeJan 31st 2010
An idea:
Perhaps the CatLab can be an internal wiki of sorts for a much grander project. Consider Bourbaki. What could be done is: develop mathematics from scratch from a categorical point of view, like Bourbaki. The first step would be to develop a project outline: what would we want to cover over the next ten years. It's clear that the first book would be an a book about category theory based on some fixed foundations, which would be developed entirely within the book. The second book would be a development of model category theory, and categorical homotopy theory of simplicial sets. The third book would develop the theory of quasicategories, and quasitoposes, based on the previous two books. I don't know what we could cover in the fourth book, because everything opens up from there, but there's certainly plenty of ways to go that would be great to cover. We would restrict external references to a small and established list of books, not going as far as Bourbaki, but somewhat in the same vein, in that someone with knowledge of algebra and general topology could conceivably read the series without ever having to look anything up anywhere else.
I'd like to motivate this idea for a moment: For categorical mathematics, there is no Bourbaki. If you want to look up a result that has to do with (abstract) algebra (of sets) or general topology, the odds are that it's in Bourbaki. With categorical mathematics, there has been so much work published, and no real attempt to "pare it down" for new readers, really isolating the important points. There's no top-down way to learn categorical mathematics, where someone has chosen the most important ideas and developed the results from full generality. However, unlike Bourbaki, there are two advantages we have over them: a.) The internet allows us to have full discussions about contributions without having to meet at a chateau in the mountains. b.) We're not restricted to publishing in linear order. If we ever need more results from early on to prove later results, we can always add what we need to the beginning. Bourbaki took mathematics and said that they would develop mathematics as:
(Set Theory)[------------------>
What we can try to do is:
<----------(Category theory)|------------>
This is because we're not restricted to publishing in books.
I know this plan sounds crazy, since grand plans often do, but it seems like the kind of of thing that would be as foundational and powerful as Bourbaki was 50 years ago. -
- CommentRowNumber49.
- CommentAuthorTobyBartels
- CommentTimeJan 31st 2010
You're not crazy; or if you are, then we all are.
This idea (explicitly with the name ‘Bourbaki’ used) has been discussed before on the
categoriesmailing list, as well as on the n-Category Café when the nLab was first being planned.So if the CatLab does this, then lots of people will be happy, and lots of people are interested in doing it too.
-
- CommentRowNumber50.
- CommentAuthorAndrew Stacey
- CommentTimeJan 31st 2010
But can we please still have meetings at chateaus in mountains? Pretty please!
(We ought to organise our first n-conference soon!)
We also ought to finally straighten out the licenses/copyright issues. I suspect that there's no big disagreements on these, but I think it would help make sure the ground is firm before we start building. But I don't want to distract here from the discussion on CatLab and there's already a good thread on the Forum for copyright/license stuff.
-
- CommentRowNumber51.
- CommentAuthorjoyal
- CommentTimeJan 31st 2010
@Hingi: Yes, the internet is making a big difference. Learning is as much a parallel process as it is linear or serial. The organisation of knowledge in nBourbaki (=newBourbaki) should not be strictly linear. It should be possible (and recommended) to learn by moving back and forth between different parts. Mathematics can be learned from many angles, once the basic notions of set theory are understood. Not everything should depend on category theory. For example, the basic aspects of universal algebra can be explained without category theory. Quite the opposite, category theory makes sense only with a variety of examples: we need to be familiar with groups and homomorphisms, with rings and homomorphisms, with metric spaces and continuous maps, etc. Category theory is everywhere but not everything is categorical.
-
- CommentRowNumber52.
- CommentAuthorTobyBartels
- CommentTimeJan 31st 2010
Mathematics can be learned from many angles, once the basic notions of set theory are understood. Not everything should depend on category theory.
I just want to add: Not everything depends on set theory either.
-
- CommentRowNumber53.
- CommentAuthorjoyal
- CommentTimeJan 31st 2010
I think that category theory depends on set theory. A category is a set of objects together with a set of arrows. Of course, these sets can be of a primitive kind. We dont need the full power of Cantor set theory to consider a set. One can also consider a category internal to another category, but the ambiant category has a set of objects and a set of arrows.
No one shall expel us from the paradise that Cantor has created for us.
wrote David Hilbert. Even Martin Lof type theory depends on set theory, since it is all about a set of types, together with a set of terms. It seems very difficult to escape the paradise that Cantor has created for us. But why should we try? Mathematics works very well with set theory. This includes category theory and higher category theory.
-
- CommentRowNumber54.
- CommentAuthorTobyBartels
- CommentTimeJan 31st 2010
A category is a set of objects together with a set of arrows.
We had a long discussion on the
categorieslist about this, so you already know that I don't agree.Even Martin Lof type theory depends on set theory, since it is all about a set of types, together with a set of terms.
This is false.
-
- CommentRowNumber55.
- CommentAuthorjoyal
- CommentTimeJan 31st 2010
list about this, so you already know that I don't agree.
I am sorry, I have missed your argument. Would you mind recalling it?
This is false.
Let me be clear: I am not saying that Martin Lof type theory depends on the full power of Cantor set theory. A set is a collection of objects with an equality relation.
-
- CommentRowNumber56.
- CommentAuthorTobyBartels
- CommentTimeFeb 1st 2010
Sorry for my terse post up there; I wrote it while I was dashing off elsewhere. Let me say it like this:
A category is a set of objects together with a set of arrows.
There was a long discussion on the
categorieslist recently, as you'll recall, which touched on evil and the relation of smallness to strictness. If you want to do category theory in a language which avoids evil entirely, then in fact the objects will not form a set as such, although they will still form a preset (or type, or sort, or whatever you call it). Nevertheless, I don't really mean to imply that you can do category theory without doing set theory, since hom-sets are still sets, and sets are still discrete categories.Even Martin Lof type theory depends on set theory, since it is all about a set of types, together with a set of terms.
A set-valued model of Martin-Löf type theory has a set of types, but you don't have to understand anything about sets to understand the syntax of type theory and use it. You might as well say that type theory depends on infinity-groupoid theory, since it has interesting infinity-groupoid-valued models as well. Or say that a set theory like ZFC or ETCS depends on a prior set theory, since it also has set-valued models. Or conversely, say that set theory depends on type theory, since you can do constructive model theory in Martin-Löf's framework as well.
-
- CommentRowNumber57.
- CommentAuthorTobyBartels
- CommentTimeFeb 1st 2010
When I said that not everything depends on set theory, I was really thinking of things like arithmetic and Euclidean geometry. Some deep results depend on connections to other fields that are based on set theory, of course the model theory is based on set theory, and a rigorous concept of real number effectively depends on set theory; nevertheless, mathematicians before the 19th century did fine without it.
So not to disrespect the fundamental importance of either set theory or category theory, but not all of mathematics relies on either of these.
-
- CommentRowNumber58.
- CommentAuthorDavidRoberts
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
I second Andrew's call for conferences in chateux. What with the panel discussion coming up, why not have our own conference? Would acquiring funding from an official body be an option? But maybe this point should have its own thread. -
- CommentRowNumber59.
- CommentAuthorjoyal
- CommentTimeFeb 1st 2010
I guess that our divergence of opinion is more philosophical than mathematical. Philosophical discussions tend to be endless. I mostly care about mathematics. I hope we can have a good philosophical discussion if we meet in some future.
-
- CommentRowNumber60.
- CommentAuthorHarry Gindi
- CommentTimeFeb 1st 2010
The choice of foundations is literally the least important part of the project, as long as we have AC. -
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
I keep changing my conception of the CatLab. It is now becoming more like Bourbaki. Maybe it should have a different name.
That's how it goes with these projects. It is very hard to know and plan in advance what they will be like. They will develop life of their own. That's why I am glad you asked for creation of the CatLab and that we created it.
I now think that it should contains a full description of categorical mathematics, including proofs. It will need an editorial board, because there will be important choices to make. If peoples dont like the choices, they will be free to create another CatLab with a different editorial board. The general public is best served when there is a variety of organisations competing to offer a service.
I can believe that this is quite certainly true. Maybe one should however think about to which degree the public is served by fragmentation of communities. For instance if there are a handful of competing choices for how to define some concept, is it best to have each definition live in its own web, or maybe better to have them all on one single page devoted to that concept, clearly indicated as different perspectives?
-
- CommentRowNumber62.
- CommentAuthorHarry Gindi
- CommentTimeFeb 1st 2010
@Urs: There is a reason why in writing something like this, a group should adopt a fixed and united viewpoint on the topic. To keep everything accessible and proofs uniform, it's a really good idea to fix a specific viewpoint and work from there. Luckily, with category theory, as long as you accept the axiom of choice, the foundations can be "hotswapped", because they all build up the same set theory in terms of how the proofs are done. Unless I misunderstood your point. -
- CommentRowNumber63.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
Maybe I can turn this around:
I would be very interested in hearing which nLab entries on category theory Andre Joyal regards as having adopted a wrong point of view to the extent that there is no way to edit them to bring them in better shape. It is this kind of discussion which is very fruitful, both for authors of an entry as well as for readers of the final result. I believe in the long run a small number of webs with a large amount of interaction between different viewpoints will be more useful for humanity than a large number of webs with small amount of interaction between their different viewpoints.
Of course there is a limit to which it makese sense to have differing approaches meet each other. But I think given that we are all speaking about points of view within the general point of view of category theory, we are in a sufficiently restrictive context already to make differing viewpoints fruitful.
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
By the way, concerning formatting:
to have definition/theorem/proof -contexts typeset nicely, there are special commands to typeset these, described here:
-
- CommentRowNumber65.
- CommentAuthorjoyal
- CommentTimeFeb 1st 2010
Urs wrote:
I can believe that this is quite certainly true. Maybe one should however think about to which degree the public is served by fragmentation of communities. For instance if there are a handful of competing choices for how to define some concept, is it best to have each definition live in its own web, or maybe better to have them all on one single page devoted to that concept, clearly indicated as different perspectives?
Unfortunately, today's mathematics is fragmented. Possibly because mathematical knowledge has expanded enormously during the 20th century. Few peoples are now able to cross the walls between different fields. This is bad, since the solution of a problem in one field may depends on knowledges outside the field. But a movement toward the unification of mathematics has emerged during the last decade. This can be seen in the intricate weaving of geometry, category theory, homotopy theory and higher category theory. The nLab community is presently working to assemble the different pieces so that they can be used for research and education. The goals of nBourbaki should not be different, but it may differ by the means. I think that the nLab should concentrate on research and nBourbaki on education. Many students are suffering from not having access to a unified and comprehensive exposition of mathematics. Graduates and undergraduates should profit from nBourbaki. A myriad of mathematics students in the developing countries may eventually use it. We should have a long term plan, at least 20 years long. The mathematicians of tomorrow are today's students.
nBoubaki should present a unified exposition of mathematics, from Euclidian geometry to higher topos theory. It should use category theory when useful without imposing it. It should use Cantor set theory as a foundation of mathematics because it is an established standard and because category theory based on set theory is working very well. Convincing peoples to use category theory is more important than giving mathematics a categorical foundation which is non standard and debatable.
I believe that nBourbaki should be structured as a journal with an editorial board and an editor in chief. This is necessary for presenting a unified point of view on mathematics. I hope that one could submit a contribution by writing it down directly as a wiki. The author of a contribution which is accepted for publication should be rewarded with some kind of official recognition.
nBourbaki is just a dream at the moment. It will become real only if it is a common dream. Its realisation will depend on the participation and support of the nLab community.
-
- CommentRowNumber66.
- CommentAuthorMike Shulman
- CommentTimeFeb 1st 2010
@Andre: Would it be too radical to suggest that nBourbaki need not be explicitly wedded to any particular foundation of mathematics?
@Harry: (Un)fortunately, not all of us are content to adopt the axiom of choice.
-
- CommentRowNumber67.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 1st 2010
I'd like to second Mike #66 on his second point; more exactly, I prefer not to commit myself to adoption of AC, but adopt a local axiomatic approach where sometimes I'll happily assume it, sometimes not.
On top of Mike's first point: I'd prefer not to worry about "turf": I view the dividing line between education and research as somewhat artificial. Until nBourbaki really gets up and running and I like how it's being managed, I will probably continue writing articles for nLab even if they seem more educational than research-oriented. On the other hand, it would fine by me if someone working on nBourbaki wants to import anything I've written and rework it for nBourbaki; the keyword is cross-fertilization.
On a more personal note, one thing I really like about nLab is the relative anarchy: work on what you jolly well please, but try to behave in a cooperative spirit. I fear that I would chafe under an editorial board at nBourbaki telling me how to write. I'm not guaranteeing that would be my reaction, but it would be a worry. (I can understand why editorial oversight and centralized advance planning would be thought desirable, but for my money the spirit of cooperation on nLab is solid enough that there hasn't yet been a strong need for it. That could change of course.)
-
- CommentRowNumber68.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 1st 2010
<div> <p>While I'm at it: I strongly agree with Urs at #63:</p> <blockquote> I would be very interested in hearing which nLab entries on category theory Andre Joyal regards as having adopted a wrong point of view to the extent that there is no way to edit them to bring them in better shape. It is this kind of discussion which is very fruitful, both for authors of an entry as well as for readers of the final result. I believe in the long run a small number of webs with a large amount of interaction between different viewpoints will be more useful for humanity than a large number of webs with small amount of interaction between their different viewpoints. </blockquote> </div> -
- CommentRowNumber69.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
@Todd, the whole editorial board thing would probably actually be like the way Bourbaki worked, if you're familiar with their editorial practices. If you're not, that means that editorial discussions would be relatively anarchic anyway. Bourbaki manuscripts weren't produced because people were tasked with writing certain parts, but rather, they volunteered to write certain parts, which were ranked by importance.
Regarding AC, could we put a little mark or notice, perhaps, on any result that relies on any result relying on AC? That seems like a happy compromise. -
- CommentRowNumber70.
- CommentAuthorjoyal
- CommentTimeFeb 2nd 2010
@Mike: I was an adept of constructive mathematics during a decade (around the 70's). I used to love it. I used constructive reasoning for proving results in topos theory instead of using standard categorical arguments. But by the end of the 70's, I got tired of constructivism. Not only because constructive mathematics is more complicated than classical mathematics, but also because I felt increasingly isolated. There was very few peoples with whom I could discuss. I recall announcing triomphantly to my collegues that I had found an example of a (real) polynomial of degree 3 with no real roots. They thought that I was becoming bizarre. I was surely belonging to a sect. We were living in a different universe. It was better to tell them that I had constructed my example in an elementary topos, because they could at least understand in principle my statement. Some concluded that toposes were not worth further considerations! I now think that the only way we can convince other mathematicians that category theory is good is to put ourselves on their ground and use category theory for proving a new result in their fields. This is hard, but there is no alternative really. A purely category foundation to mathematics will not change their attitude unless they really need it. The recent developement in higher topos theory is no guaranty of a bright future, unless it brings new results in "ordinary mathematics".
There is really no absolute conflict between the constructive and non-constructive approaches to mathematics because they are mutually interpretable. Constructive mathematics can be interpreted in classical (non-constructive) mathematics, since an elementary topos is a classical object. Conversely, ZF-set theory is a structure within constructive mathematics, since it is a certain formal system. Of course, these interpretions do not respect the intended meaning of these theories, but this is a different issue.
The relation between constructive and non-constructive mathematics can be compared to the relation between euclidian geometry and hyperbolic geometry. The two geometries are mutually interpretable. The Klein model of hyperbolic geometry is the unit disk of the euclidian space. Conversely, a horosphere in hyperbolic space is an euclidian plane. An imaginary person living in hyperbolic space may argue that hyperbolic geometry is more fundamental than euclidian geometry because physical space is hyperbolic. But it should not take long to these imaginary peoples to discover that euclidian geometry is much simpler than hyperbolic geometry. It has certainly more symmetries with the group of similitudes. They will eventually discover the Klein model and consider that euclidian geometry is mathematically more fundamental. Actually this tale is not entirely imaginary since it can be applied to us. We have discovered that the notion of a vector space is simpler than that of an euclidian space. It certainly has more symmetries with the general linear group. This is why modern euclidian geometry is best described from linear algebra.
If Cantor set theory has been widely adopted by the mathematical community it is probably because the basic notions of set theory seems clear and simple. You may regard it as an illusion and think that constructive mathematics is more real. Probably that both are illusion! But one of them is simpler, like euclidian geometry. I find it easier to understand things non-constructively first. The constructive aspects come after, as a kind a refinement.
L.E.J. Brouwer may turn over in his grave.
-
- CommentRowNumber71.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
To expand a little further on my idea: the work could be offered in a constructive and classical flavour (if people insist), where all of the nonconstructive bits are edited out in one edition, and one where they are only marked with a little "AC" symbol.
The fact is: the classical approach is easier in general, so if a classicalist (classicist?) writes a part and a constructivist offers a constructive proof, the constructive proof should always be used, but where no proof exists, the classical proof stays. That way, we have the "best possible" constructive book, while also having a book that is not limited by the constructive approach in places where the constructive approach leaves things unprovable. -
- CommentRowNumber72.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 2nd 2010
Harry, I more or less agree with your suggestions regarding AC, but in fact that's what has essentially already happened in many pages on nLab: various people point out where AC is being used, and workarounds where they exist. I haven't made a systematic study to back up this claim -- it's just my perception -- but if you spot any counterexamples then they should definitely be brought up in comments and query boxes.
-
- CommentRowNumber73.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
@Todd: I'm not referring to the nLab, though. I'm talking about this grand project that we're trying to model after Bourbaki. The whole problem with nLab is that it's a useful reference, but you can't systematically learn categorical mathematics just by reading nLab. In fact, I'm speaking somewhat from experience. I've always thought there should be a bourbaki-like project to continue their work into categorical mathematics, which is exactly what Grothendieck was doing before he quit mathematics in the early 70s. He wrote one or two chapters (And you know Bourbaki chapters, they're frequently a hundred pages or more) of a book on category theory from the Bourbaki viewpoint. The only reason why I never proposed a project is because I'm just an undergraduate student with no real way to talk with you guys on an equal footing, and as such I don't really think it's my place to suggest a "grand project". However, since it's been brought up by someone much more respectable than myself, I am very enthusiastic about such a program. -
- CommentRowNumber74.
- CommentAuthorTobyBartels
- CommentTimeFeb 2nd 2010
What we really need more of in this world are things that are easier in nonclassical approaches. Like André's colleagues from the '70s, I'm not much interested (only a little interested) in an odd-degree real polynomial with no real root. But would definitely be interested in proving a theorem that every function
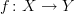 between Banach spaces is continuous. (I know a theorem in one nonclassical framework that applies when
between Banach spaces is continuous. (I know a theorem in one nonclassical framework that applies when  has finite dimension, and I know a theorem in another nonclassical framework that applies when
has finite dimension, and I know a theorem in another nonclassical framework that applies when 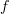 is linear. It would be interesting to combine these frameworks, check that the result is consistent, and see if the general theorem can be proved. Of course the theorem holds classically only when
is linear. It would be interesting to combine these frameworks, check that the result is consistent, and see if the general theorem can be proved. Of course the theorem holds classically only when  has finite dimension and
has finite dimension and 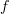 is linear.) That would make some things very easy to prove!
is linear.) That would make some things very easy to prove! -
- CommentRowNumber75.
- CommentAuthorMike Shulman
- CommentTimeFeb 2nd 2010
Andre, I think I agree entirely with what you wrote, except that I don't think that category theory needs to be explicitly founded on membership-based set theory in order to be accepted by the mathematical community. In my experience, although most mathematicians may pay lip service to the notion that membership-based set theory is the foundation of mathematics, they never use any non-structural aspects of that theory. All the categorically interesting aspects of foundations, such as AC or transfinite induction or large cardinal properties, are structurally invariant. So since membership-based ("material") and structural set theories are, as you point out, mutually interpretable (and, in the case of strong theories such as ZFC, completely equivalent), why should not nBourbaki adopt an agnostic attitude? We require certain properties of sets and functions; these properties can be assured with a number of different axiom systems, including those like ZFC that most readers will be more familiar with.
The classical/constructive question is, of course, orthogonal to the material/structural one. I was definitely not suggesting that nBourbaki adopt an overall constructivist attitude. On most days, I am not a constructivist, philosophically speaking; my main interest in constructive arguments is because they remain valid in arbitrary topoi. I also think that constructive and AC-free proofs tend often to be cleaner and more illuminating, when they exist, and I don't see any harm in quietly preferring them whenever possible, as Harry suggests. I also feel that the possibility of applying internal categorical logic to the study of many different categories (not just topoi, but quasitopoi, pretopoi, regular and exact categories, perhaps even monoidal categories with linear logic) is one of the more unexplored things that category theory has to offer the rest of mathematics. And once one wants to start applying this idea, of course one is inexorably forced to consider the constructive validity of various arguments. But it will certainly take a gradual and careful attitude to convince most mathematicians that this is worthwhile.
-
- CommentRowNumber76.
- CommentAuthorjoyal
- CommentTimeFeb 2nd 2010
Many thanks to all of you, Urs, Toby, David, Mike, Todd and Harry. This was a good conversation. I will think about what you said during the next days. I should return at the weekend. Bye
-
- CommentRowNumber77.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
The whole problem with nLab is that it's a useful reference, but you can't systematically learn categorical mathematics just by reading nLab.
But that's a "problem" with the current state of the nLab, not with its nature. As soon as somebody finds the energy to put more expository category theory into the nLab entries, then there it is!
For example currently also one cannot learn much about homological mirror symmetry on the nLab, much as I regret it. But that's not because somehow by its nature the nLab cannot have entries on homological mirror symmetry so that we'd need a MirrorSymmetryLab. It's just because nobody so far found the energy to put them in.
I, for one, put into the nLab the expository material that I happen to need. Right at this time and in the weeks to follow, I am brushing up and inserting expository material on (oo,1)-category theory as I need it for a Seminar on (oo,1)-Categories and oo-Stacks. This is designed to satisfy some people's expository needs. And it will be good to have that material sitting within the nLab proper, with all the hyperlinks from and to it. That makes it much more valueable than if it were isolated on my private web.
If you are feeling you lack a certain aspect of the nLab, then in general you have two options: either put it in yourself or try to bug other people in a way that they will eventually put it in. Start asking us questions on category theory. Before long, the answers will generate expository content at the corresponding entries.
-
- CommentRowNumber78.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
For instance, a while ago Eric Forgy felt like starting some basic expository pages on category theory, for his own good. From that we have entries such as
Nothing to stop us from expanding this further.
-
- CommentRowNumber79.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
I feel like the structure of nLab is not conducive to the type of project I'm talking about. nLab is wonderful. It changes with the times. It's frequently updated. It has a wide range of subjects and topics. However, it is not "ordered". All of the ideas are thrown at you at once. There's no list of dependencies for each article. With a book-type project, we can linearly order the material and leave out some information until later, avoiding an explicit "list of dependencies" reference at the bottom of the page.. The exposition would be connected and cohesive. These are things that we can't expect on nLab. nLab has another role to fulfill. The two projects are completely free of overlap. -
- CommentRowNumber80.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 2nd 2010
Harry -- sorry I misunderstood that you were talking about a new lab like CatLab, not nLab, with regard to AC.
I agree that it may be hard to learn mathematics from nLab at its present stage of development, but I also concur with Urs that I see nothing in the essence of nLab that would prevent its becoming a great learning tool. (If Wikipedia can be a great tool for learning math -- and I think in many ways it is -- then so can nLab.) I for one would love for someone like you (or others with less knowledge; you already seem to be fairly sophisticated) to ask more questions which would tend to develop exposition. We could use your help!
I strongly disagree that exposition can't be connected and cohesive on nLab, and even more that the two projects are completely free of overlap. nLab is still new and with a small group of active participants. It's far too early to judge what roles it can possibly fulfill.
-
- CommentRowNumber81.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 2nd 2010
<div> <p>@Harry at # 69:</p> <blockquote> the whole editorial board thing would probably actually be like the way Bourbaki worked, if you're familiar with their editorial practices. If you're not, that means that editorial discussions would be relatively anarchic anyway. Bourbaki manuscripts weren't produced because people were tasked with writing certain parts, but rather, they volunteered to write certain parts, which were ranked by importance. </blockquote> <p>I've read a bit about their practices from casual reading. My understanding is that yes, someone would volunteer and write up a draft of a chapter, some exposition, read it out loud, and then the others would basically tear it to shreds. The milieu appears to me to have been hypercompetitive, continuing the atmosphere they grew up in (most of them) at the Ecole Normale or some such place. I hope CatLab or nBourbaki wouldn't be like that! ;-)</p> <p>More seriously, it sounded to me that Andre had in mind something more tightly managed from above than that, but he can tell us more about his conceptions as we go along.</p> </div> -
- CommentRowNumber82.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
The problem with the Bourbaki approach is that it was before its time. It is suited wonderfully for the internet for all of the reasons it is a bad choice in person. So much of what Bourbaki did in terms of editing is already included in the way nLab works, i.e., any changes you make are reflected on the nForum anyway. You could say it's the natural evolution, of the approach, to some extent.
I think that what Prof. Joyal is trying to do is take the nLab approach (internet collaboration with high levels of communication) and fuse it with the Bourbaki approach of writing a completely independent treatise on categorical mathematics as a whole, with all proofs and references internal to the work (like Bourbaki). That is, it wouldn't just be a reference, but rather a comprehensive reference, picking up where Bourbaki left off after Grothendieck stopped writing his book on category theory. Something like a continuation of the grand project. I think that this is a necessary to bring category theory fully into the spotlight as a fundamental part of mathematics. That is, if we don't do something about it, nobody will. Just look at the homotopy theory community. Apparently, (infinity,1)-categories have been well-known objects within the homotopy theory community since the 1970s and 1980s, but they only came to light after Rezk, Joyal, Lurie, etc. actually began to publish work on them. The problem is, the requirements for someone to learn all of these things is actually fairly steep. Not only does one have to learn ordinary category theory, but also homotopy theory and model category theory. The advantage of an integrated Bourbaki-esque approach like Prof. Joyal is advocating is that we can pare these subjects down to the essentials in order to develop higher category theory. The reason why doing this on nLab is a bad idea is that we'd cut out extraneous details, whie on nLab, these details should be included because they're important. References to other works that study certain topics in detail are also very important, but for an integrated project, these have to be eliminated completely or relegated to a "suggested reading" list like in Serge Lang's algebra book. Trying to build nLab and nBourbaki on the same platform would be counterproductive for both efforts. -
- CommentRowNumber83.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
I feel like the structure of nLab is not conducive to the type of project I'm talking about. [...] it is not "ordered".
It may be pointless for me to continue replying to this, and I apologize for filling up this thread here, but when I hear such statements I feel like a father hearing casual bypassers complain about his 3-year old son: "Bah, he can't do that, he doesn't even know this, we'll not bother with him." It's hard to remain silent then. I feel there are several assumptions and conclusions wrong with these statements.
For instance: there is plenty of effort at the nLab on bringing order into the material. We have floating tables of contents accompanying entries on core topics, for instance. And notably we have entire textbooks equipped with keyword lists. Have a look at Stone Spaces or Higher Topos Theory, to name just two of a list of examples. Or have a look at our lecture series A Survey of Elliptic Cohomology, neatly ordered into a dozen or so chapters.
I am not claiming that these pages necessarily satisfy what one might hope for: very few pages on the nLab are already in a form that I would call fully satisfactory. I hope with time it will improve! But if an example is needed that ordered exposition is possible on the nLab, then these are some.
And why shouldn't it be possible? Why should a large repository of entries prevent anyone from starting more book-like pages? In general, if you think about it, there is very little indeed that a wiki such as the nLab can not be. It's possibilities are pretty boundless.
Of course it needs somebody to realize it. And of course the community spirit needs to suit those who would like to contribute. The main message that I get here is that the current community spirit of the nLab regulars is beginning to look non-inviting to newcomers. Originally it was intended as being the accumulation point for a plentitude of contributors. I have to accept that this is not what is happening and that eager contributors rather feel like working in their own niche. But I feel I need to interfere against public statements of the form "The nLab can't be this and can't be that" which are suited to discourage the lurking reader who was just about to create his or her first page on the nLab.
All that said, i should add that the "nBourbaki"-vision being promoted here sounds really good. It reminds me a whole lot of the way we conceived the nLab-vision, though it may be more restrictive in its aim, and therefore more focused. I certainly expect that Andre Joyal's presence will attract more contributors than we could, and I am eagerly looking forward to the point to see it filled with activity. If really a nontrivial number of category theorists could be motivated to contribute here, that would be quite exciting.
-
- CommentRowNumber84.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
Perhaps I spoke too soon. If I'm mistaken, please correct me, given that you're probably the most active contributor to nLab and know the site better than anyone else here. Also, I'm extremely new here, so I'm totally happy to defer to someone who knows better.
To answer your one question about book pages in a large repository of entries: You can build a bakery in the middle of a toy factory, but it's not really optimal for the bakery or the toy factory. (I hope my metaphor was clear enough. My metaphors aren't usually very good.) -
- CommentRowNumber85.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 2nd 2010
One thing I want to see more of in nLab, and which André explicitly pointed to as a desired feature for CatLab, is proofs. We have a lot of definitions and statements of theorems, somewhat like those old Encyclopedias of Mathematics, but it can be very hard to extract insight from that alone. (To be fair, there is also a fair amount of effort to provide intuitions and motivation here in nLab, which is absent from those Encyclopedias, but yet much more is needed.) We also need much more in the way of worked examples in nLab.
-
- CommentRowNumber86.
- CommentAuthorTim_Porter
- CommentTimeFeb 2nd 2010
The point Harry made (I quote) "(infinity,1)-categories have been well-known objects within the homotopy theory community since the 1970s and 1980s, but they only came to light after Rezk, Joyal, Lurie, etc. actually began to publish work on them" does not quite give the right information. Cordier followed up the earlier work of Vogt and came out with the homotopy coherent nerve construction and then he and I worked and published on Vogt's theorem and homotopy coherent diagrams. We had actually worked on what are now known as quasicategories and would have given a more detailed treatment except that requests for funding failed to get success and even attempts at publication got very strange negative vibes. In other words, the mathematical world was not ready for that theory!!!! Seriously, our reasons for studying it were at the same time Strong Shape Theory and Grothendieck's Pursuing Stacks and in the UK neither was well regarded.
-
- CommentRowNumber87.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
Sorry about that, thanks for the real story. You should write a little historical article detailing the early history of the subject, so people won't make the same mistakes I just made. -
- CommentRowNumber88.
- CommentAuthorTim_Porter
- CommentTimeFeb 2nd 2010
Don't worry. My only point is that if you have excellent ideas before the adjacent infrastructure is there, then your work although notable may not be noticed. It is because of that that n-lab and related cafés blogs etc, is so good. It can be disheartening to do good work and then have it ignored (or sometimes denigrated!) by the people you were hoping it would be useful for.
By the way, Heiner Kamps and I did a low key intro to homotopy coherence in a textbook (Abstract Homotopy Theory...) and you might find it usefulfor getting some ideas about the quasicategorical viewpoint.
-
- CommentRowNumber89.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
Thanks! I'll check it out.
@Urs: I would say that the difference between nLab and this other project is something like the difference between Seminaire Bourbaki and the Bourbaki book writing project. Seminaire Bourbaki covered the latest and most advanced stuff of the times, while the regular books, to quote Dieudonne, "..., those which Bourbaki proposes to set forth are generally mathematical theories almost completely worn out already, at least in their foundations. This is only a question of foundations, not details. These theories have arrived at the point where they can be outlined in an entirely rational way." -
- CommentRowNumber90.
- CommentAuthorMike Shulman
- CommentTimeFeb 2nd 2010
There is definitely a difference between something that is written as a textbook and something that is written as a reference. One can learn a lot of math reading Wikipedia and the nLab, but I think there's also something to be said for reading a carefully designed linear exposition of a particular topic. For all that mathematics itself is not linear, the process of reading is linear, because the time axis of spacetime is one-dimensional. (-:
Of course, as Urs says, there's nothing preventing such a book from existing as part of the nLab. But I think if such a book were to be written, it would be good to clearly separate pages that are "part of such-and-such book" from the main collection of pages. It makes sense to have the main page on X concept be aimed at the random mathematician following a link from somewhere else on the web and who just wants to know about X concept (along, of course, with how it relates to other things that s/he could follow links to), versus a book chapter about X which will assume the reader has read the previous chapters in the book and lead forward to the following ones.
Regarding proofs, I think one of the virtues of many of the nLab pages is that they give an overview and intuitive picture of a topic without delving into long and complicated proofs. Sure, it would be even better to have the proofs accessible, but often I think if there's a proof we want to include that's longer than a few lines, I'd prefer to have it on a separate page rather than disrupting the concise flow of the main page. Like a "zoomable" approach to understanding math: one page has the big picture, then if you want more details on part of it, you can go in further to some proof, or follow a link to some other concept.
-
- CommentRowNumber91.
- CommentAuthorTobyBartels
- CommentTimeFeb 2nd 2010
On the linearity of textbooks:
To avoid reinventing the wheel, take a look at some of the discussions from the first few months of planning Wikibooks in 2003, specifically those with ‘getting to work’ or ‘linearity’ in the subject header in June and July.
In particular, there was a specific proposal for great flexibility, never implemented, given by Daniel Mayer and modified by me. It would be cool if we could do that, which Wikimedia never did, even though many people wanted to in those heady early days.
-
- CommentRowNumber92.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 2nd 2010
<div> <p>Mike, in your last paragraph it sounds like you're responding to my last comment.</p> <blockquote> Regarding proofs, I think one of the virtues of many of the nLab pages is that they give an overview and intuitive picture of a topic without delving into long and complicated proofs. Sure, it would be even better to have the proofs accessible, but often I think if there's a proof we want to include that's longer than a few lines, I'd prefer to have it on a separate page rather than disrupting the concise flow of the main page. Like a "zoomable" approach to understanding math: one page has the big picture, then if you want more details on part of it, you can go in further to some proof, or follow a link to some other concept. </blockquote> <p>Well, yeah -- that's the advantage of hyperlinks. And that's all I was saying: there should be <em>lots</em> of such separate and linked pages, for proofs and worked examples.</p> </div> -
- CommentRowNumber93.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
I guess what I'm talking about is slightly different. Rather than making it a wiki, use the wiki as an SVN-type of thing that also supports discussion and commenting on any part of a page. Then periodically put out new versions when sections are deemed finished. It would be something like a cross between Stacks-GIT and Bourbaki. -
- CommentRowNumber94.
- CommentAuthorMike Shulman
- CommentTimeFeb 3rd 2010
@Todd, yes that was in response to you. I wasn't sure exactly what you were proposing. Sounds like we agree.
-
- CommentRowNumber95.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 3rd 2010
I'm glad we agree, Mike. This zoomable approach to exposing and learning mathematics has actually been a pipe dream of mine for a long time, and I hope we can implement it (more and more) on the nLab.
-
- CommentRowNumber96.
- CommentAuthorjoyal
- CommentTimeFeb 3rd 2010
@Urs: I had a good night sleep. I now think that changing the name of the CatLab to nBourbaki was premature. Essentially because nBoubaki should be created by a group of peoples, not by the decision of one person. This is how Bourbaki was created initially and this is how it should work. The key is to have a group of peoples working in different fields sharing the same vision of mathematics and education. The discussions of the last few days are showing that the nBourbaki idea is exciting and that it may be created in the future. But the creation of a group like Bourbaki probably depends on a variety of factors that are difficult to identify and hard to reproduce. The only thing we can do is to work in the right direction, hoping that something like nBourbaki will eventually emerge. In a sense, this is what the nLab is already doing and I hope that the CatLab will contribute. I am grateful to the nLab community for supporting the CatLab. I keep thinking that the CatLab should concentrate on making polished expositions, and that it may eventually have an editorial board. I will be working alone in the CatLab for a while because I would like to feed it with my personal notes, some are quite extensive and they often need corrections. The nLab is a wiki for collaborative work in mathematics, physics and philosophy and it works very well as it is. It could leave the polished expositions to the CatLab, but it is up to the nLab community to decide. Yours, --André
-
- CommentRowNumber97.
- CommentAuthorUrs
- CommentTimeFeb 3rd 2010
because I would like to feed it with my personal notes
This would be highly appreciated, I am sure, by many people. I am very much looking forward to see this.
I also like how you think about the general matters of what your web could be. I am very open to all of these ideas.
(The only point that I objected to in the above discussion -- not made by you -- and that I will keep objecting to, are sweeping statements along the lines this-and-that-can't-work on this-and-that-web. For what we are doing here it is all-important that people -- like you -- go ahead and follow talk with action. As we see here, what works and what does not work is only seen after trying it out.)
It could leave the polished expositions to the CatLab
Sure. In the end the difference to the end user between a page on this web or on that web is marginal -- after all it is just a difference in what the server takes to be the URL, really. The distinction between the webs is of much more importance for the psychology of the people working on them, as I think you essentially pointed out. Some entries will develop more easily in a place that is marked appropriately. Notably currently we all have our personal webs precisely to develop material there that for some reason does not feel as if it should be developed on the main nLab. But an entry on a personal web may eventually stabilize and be linked to from entries on the main nLab and gradually become part of it that way, or it may even be copied into a genuine nLab entry. That happened before.
So I'll be following whatever you develop on the CatLab with great interest. Once something stable has emerged, we can still think about how we want to link to it, or if we want to copy it somewhere else, or not.
-
- CommentRowNumber98.
- CommentAuthorAndrew Stacey
- CommentTimeFeb 3rd 2010
(@Todd and Mike: Leslie Lamport (of LaTeX fame) had some ideas about this - zoomable proofs, that is. I don't remember off-hand where I came across them but a search should turn up something. I like the idea very much and would love to see this happen on the nLab. I've been thinking a little of reorganising the material on the Froelicher space page to be more hierarchical and creating subpages as appropriate. But time and tide ...)
-
- CommentRowNumber99.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 4th 2010
I remember reading some of Leslie Lamport's stuff on this. IMHO he takes this much greater extremes than I'd be willing to do for nLab -- really, really formal nitty-gritty levels of detail. But I'm glad you like the basic idea!
-
- CommentRowNumber100.
- CommentAuthorjoyal
- CommentTimeFeb 4th 2010
I wonder if someone could help me about Latex fonts in MatML. I would like to use ${\cal A}$ in Latex if possible. Thanks, --Andre