nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
nLab > Latest Changes: motivic cohomology as stable oo-stack cohomology
Bottom of Page1 to 12 of 12
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
- (edited Jan 20th 2010)
I added to motivic cohomology the definition of motivic cohomology in terms of connected components of hom spaces in (the homotopy stabilization of) the (oo,1)-topos of oo-stacks on the Nisnevich site.
This is now the section Homotopy localization of the (oo,1)-topos on Nis.
Probably Zoran mentioned this before, without me getting it. Now I get it, and I like it a lot. This is the kind of nice formulation of motivic cohomology that one would expect from the point of view that is expressed at cohomology:
in fact, really a priori one should consider nonabelian motivic cohomology, by considering genuine oo-stacks on Nis, without stabilizing. One could consider differential Motivic cohomology by not retricting attention to the homotopy localization .
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
created Nisnevich site
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
expanded the "Idea"-section at cohomology:
the first new paragraph is the one beginning with the words "Starting with an unconstrained..."
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
more references at Nisnevich site and motivic cohomology and A1-homotopy theory
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
I rearranged the structure of motivic cohomology a bit:
in the introduction, after the first sentence, I say that several proposals exist, and then list the different definitions (currently two) with a brief comment and a pointer to the corresponding subsection.
The introductory sentences on the Voevodsky definition that used to be in the main Idea-section I moved now to the corresponding subsection.
I also moved the section on the Morel(?)-definition in terms of oo-stack cohomology on Nis to the top now, and pushed Voevodsky's definition down. Morel's one is the nice one that follows the general pattern as described at cohomology: we have an oo-stack oo-topos
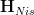 and for X and A objects in there, the motivic cohomology of X with coefficients in A is just
and for X and A objects in there, the motivic cohomology of X with coefficients in A is just 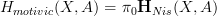 .
.For the standard definition of motivic cohomology the objects A here is required to be stable and homotopy invriant. For general A we could call this "nonabelian motivic cohomology", I suppose.
To emphasize this (nice, I think) point, i have included a section on how Chow groups appear from this perspective, by copy-and-pasting a nice summary by Denis-Charles Cisinski from MathOverflow:
effectively, for
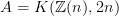 an Eilenberg-MacLane object in
an Eilenberg-MacLane object in 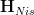 , the Chow groups of some X is just the corresponding "ordinary" cohomology of X in
, the Chow groups of some X is just the corresponding "ordinary" cohomology of X in 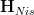 , namely
, namely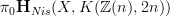 .
.I should say that I was in the middle of proof-reading and polishing my edits when suddenly the entry was locked -- by Toby! :-)
So I supoose Toby is doing the remaing polishing and proof-reading right now...
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
I just fixed an annoying typo that prevented some math from rendering.
Now Zoran is proofreading. (^_^)
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Now Zoran is proofreading. (^_^)
Yes, thanks to you all. I managed to make a few more corrections somewhere in between, after all.
I have notified Denis-Charles Cisinski about this at MathOverflow. Maybe with a little luck we can get him to proofread a bit, too! :-)
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
In order to side-support (for now) the motivic party, I added an entry on Alexander Beilinson...and stub BBDG decomposition theorem (a digression from Beilinson, and wall crossing which I intend to write soon, and many other thoughts in this area). Bio entry Ofer Gabber.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Thanks, Zoran. i think I am getting the hang of the motivic thing now.
I was finally pushed in the right direction by a conversation with Neil Strickland over a beer after my first talk on path-structured (oo,1)-toposes in Sheffield, yesterday.
He said this reminded him of motivic cohomology. I replied: hm, but Voevodsky's definition looks very different! To which he said: sure, but Morel's definition is the right one, and that does looks like this.
And indeed, it does. Smooth (oo,1)-toposes being in particular oo-stack oo-toposes with a line object are the same kind of setup as used in A1-homotopy theory, only that it allows more general choices of site.
And in fact, one could take this point of view: where A1-homotopy theory in particular and homotopy localization in general divides out the line object, in a sense, restricting to those objects that regard the line as being contractible to the point, instead all of "differential nonabelian cohomology" may be seen as a big tool for investigating to which degree objects fail to regard the line as contractible.
Instead of "localizing at paths" as in A1-homotopy theory, we can form the path oo-groupoid as a tool to measure how things change as we transport them along paths.
Accordingly, bundles alone are homotopy invariant (in classes), while bundles with connection are not: there is no nontrivial line bundle on the line. But there are nontrivial line bundles with connection on the line!
Anyway, this perspective helps me, personally, to get a relation to motivic cohomology. Previously it had appeared rather mysterious to me.
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Amazing picture, Urs ! In the meantime I created entry geometric representation theory. This homotopy invariance along paths -- is this something to do with the Chow moving lemma business ? I mean in lagebraic geometry one can not deform cycles, but there are kinds of equivalences (I wrote an entry some time ago on adequate equivalence relation), and there is more than one kind of Chow group, depending which equivalence you are taking. Chow moving lemma is a technical tool for this to make sense, but the relations between different adeauet equivalence relations are difficult. For example, classical hard result, the Griffiths transversality guarantees just one of such relations. I do not know if your extension would touch on such issues, if yes, than it would be hopelessly hard in practice making it working, though in some special case, who knows...
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
@Urs, is there any way we can have a convention to suppress all unnecessary (oo)s?
I added to motivic cohomology the definition of motivic cohomology in terms of connected components of hom spaces in (the homotopy stabilization of) the (oo,1)-topos of oo-stacks on the Nisnevich site.
I'd say we can lessen that to at most one (oo). Specifically, oo-stack is bad terminology, since it's nothing more than "n-sheaf" for 0<=n<=oo.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
is there any way we can have a convention to suppress all unnecessary (oo)s?
Safely? Maybe in a decade or two.
I can see that it may get annoying once in a while. But for the time being I think we'd run into much bigger trouble if we dropped the oos.
oo-stack is bad terminology
I certainly see what you mean. I was opposed to the word "stack" from the very beginning. Now I am using it a lot. Personally I would be happy to stick with, say, J. Lurie's book and just say "sheaf" or "(oo,1)-sheaf" for definiteness. But my impression is, when I talk to people and say "oo-stack" or "derived stack" they have the right associations. When I say "sheaf" they tend to think I am doing something else. It's weird, I know, but I think that's the way it is, currently.
In a few years we'll run a script over the nLab that replaces all "oo-stack" automatically by just "sheaf". Okay? :-)
1 to 12 of 12