nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Oct 14th 2014)
I added to (infinity,n)-category of cobordisms a description in plain English (or what I make of that...) of Lurie's definition of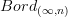 .
.
The definition is very simple and elegant, but it is not being exposed really in Lurie's writeup, and the whole definition 2.2.9, which is central to the article, is itself rather hidden somewhere, so I I am making the experience that people staring at the document tend not to see the simple point here. As a reaction to that, I thought I'd write this out now. -
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
You said you are doing in Utrecht some generalizations of quasicategory business in dendroidal sets setup. Is there a notion of STABLE quasioperad there. The stable quasicategories are naturally enriched over a standard category of spectra (omega-spectra in simplicial sets), is there a similar theorem there in dendroidal setup ?
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
Is there a notion of STABLE quasioperad there. The stable quasicategories are naturally enriched over a standard category of spectra (omega-spectra in simplicial sets), is there a similar theorem there in dendroidal setup ?
Interesting question. I don't know.
Hm, yes, I see what you mean. Will have to think about how one could define this...
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeOct 14th 2014
- (edited Oct 14th 2014)
Might anyone have a quick way to produce figures such as in figure 5 of Schommer-Pries 14 (schowing some basic morphisms in Bordfr2) for use in an nLab entry? I have tried our built-in SVG editor, but we haven’t really become friends yet.
I like these figures, but I wanted to accompany them with slightly different text that makes it clearer (or so it would seem to me) what is going on. I have started to type such text at (oo,n)-catgeory of cobordisms – Examples – Bord_2^fr. But somehow without the pictures being right next to the text the result looks a bit lame…
1 to 4 of 4