Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: principal oo-bundle

Bottom of Page

1 to 49 of 49

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeJan 21st 2010
    • (edited Jan 21st 2010)

    I expanded the discussion at principal infinity-bundle to go along with the discussion with Mike over at the blog

    • CommentRowNumber2.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    By the way, why do you systematically write deRham and not de Rham ? Is the departure from the tradition of the personal name having a deeper reason this time ?

    More serious question relating nonabelian deRham cohomology (schreiber). One thing is that using general nonsense you can define de Rham cohomology, via connection picture. Indeed this even rpesumably generalizes to noncommutative situation. U(1) bundle picture is namely something like circle action and cyclic cohomology generalizes de Rham, while cyclic sets are homtoopically those with circle action. But there is the de Rham theorem saying that the singular cohomology with real coefficients and de Rham cohomology are naturally isomorphic. De Rham theorem however is in its essence related to Stokes theorem, i.e. Newton-Leibniz-Ostrogradski-Green-Gauss-Stokes formula. Having cycles in the picture suggests also cobordisms in the picture. So how much is Stokes formula making sense from the connection point of view. And finally from infinity-topoi point of view ?

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    Many thanks for this comment, Zoran!

    First of all, I admit sometimes being funny with my notation. I don't exactly know why I started writing "deRham" instead of "de Rham". I have changed it now here and there on my web to "de Rham", thanks for pushing me.

    One thing is that using general nonsense you can define de Rham cohomology, via connection picture.

    So, that's what I am doing at that page: in quite some generality, in any (oo,1)-topos equipped with an interval object we have a notion of pricipal oo-bundle and of principal oo-bundle with flat connection. The sub-collection of flat principal oo-bundles whose underlying principal oo-bundle is trivial I identify with de Rham cocycles. In the case that the (oo,1)-topos happens to be a smooth (oo,1)-topos, these cocycles are represented by oo-Lie algebroid valued differential forms.

    and cyclic cohomology generalizes de Rham

    I have to admit that I am not yet much on speaking terms with cyclic cohomology. But I want to get there.

    It seems to me -- but I may be wrong, I need to study this more deeply -- that the general-abstract relation between de Rham and cyclic cohomology and then Hochschild cohomology is best made transparent, once again, by the Ben-Zvi/Francis-Nadler article.

    To my shame I have to admit that I might not be entirely sure that I follow the statement in full detail, but David Ben-Zvi keeps emphasizing the following, which seems to be the key insight: if we go to the derived context, i.e. to oo-stacks on cosimplicial test spaces (i.e. on simplicial rings) then starting with an ordinary space X, regarding it as a derived oo-stack and then forming its loop space object produces the derived de Rham space of X, what I call the "infinitesimal path oo-groupoid" \Pi^{inf}(X).

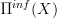    it is through this perspective, identifying the de Rham space with a loop space object, that the general abstract reasoning about loop space objects is made to apply to de Rham, notably thereby "explaining" why Hochschild cohomology may know about de Rham-cohomology, along the general lines of reasoning as in the Ben-Zvi/Francis/Nadler article. And that should also bring in the cyclic cohomology picture, I suppse.

    I want to understand this better. This is important. Thanks for pushing me.

    • CommentRowNumber4.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    Hochschild cohomology contains correct information in smooth context, on non-smooth (derived) schemes, various theorems generalizing theorems on smooth (derived) schemes need replacement of Hochschild by cyclic to work. Also the noncommutative setup likes cyclic more. Still, you missed my question above: how about Stokes formula ?

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    how about Stokes formula ?

    I understand Stokes (and its nonabelian and higher generalization) as a characterizaiton of the map that sends smooth functors 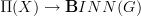\Pi(X) \to \mathbf{B} INN(G) to Lie-2-algebra ( 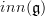inn(\mathfrak{g}))-valued differential forms. Stokes' formula exhibits that this really establishes a bijection between smooth functors and 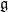\mathfrak{g}-valued differential forms: fixing these forms fixes the assignment of the functor on 1-paths. And this uniquely fixes the assignment to 2-paths, as being the suitable integral of the curvature 2-form over these.

    • CommentRowNumber6.
    • CommentAuthorzskoda
    • CommentTimeJan 22nd 2010

    I have listened a talk by Toledano-Laredo giving allusions of some nice relations between the first and third setup, nad I asked him about the slides which he promised but so far I have not gotten them. Some relations between Stokes phenomenon and stability conditions are however given in his earlier paper with Bridgeland, which I will cite now in wall crossing.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeMay 28th 2010
    • (edited May 28th 2010)

    I am in the process of polishing, expanding and refining the discussion, statements and proofs at principal infinity-bundle of the abstract notion of principal oo-bundles classified by cocycles in any (oo,1)-topos.

    Among other things I want to work out more explicitly which steps of the definitions and proofs involve the (oo,1)-Giraud axioms exactly.

    I am not done yet, but need to run now to pick somebody up from the station…

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeMar 29th 2011

    I have added to the last proof in the section general principal oo-bundles a final step (I think i had written out this step before, but it seems I have deleted it later while editing something else).

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeMar 15th 2012

    Good news: Danny Stevenson and David Roberts finally put their work on topological principal ∞\infty-bundles on the arXiv: I have added the references here.

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeMar 15th 2012

    I have added the references here.

    … and to some other entries that refer to it, notably to geometric realization of simplicial topological spaces

    • CommentRowNumber11.
    • CommentAuthorMatanP
    • CommentTimeMar 16th 2012

    Although I don’t fully understand principal infinity bundles in their most general form, I have used them in the case of topological spaces. It may be helpful to point out on a ’rigidification’ theorem in this case, which essentially follows from rigidification of loop spaces into topological groups. I’m wondering if that rigidification theorem applies to other (infinity) categories.

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeMar 16th 2012
    • (edited Mar 16th 2012)

    Yes, under very general assumptions the statement that every discrete infinity-group is presented by a simplicial group generalizes to ∞\infty-sheaf ∞\infty-toposes: every ∞\infty-group GG in the ∞\infty-topos will have a presentation by a simplicial presheaf of simplicial groups. Moreover, the corresponding delooping / classifying stack BG\mathbf{B}G will then be presented by the simplicial presheaf W¯G\bar W G. Morphisms into this model GG-principal ∞\infty-bundles presented explcitly as simplicial GG-bundles (hence “rectified” or “semi-strictified”).

    • CommentRowNumber13.
    • CommentAuthorMatanP
    • CommentTimeMar 16th 2012
    • (edited Mar 16th 2012)

    And another thing: the definition of a a principal G-action resembles what I called “homotopy action” (there is a whole section for this at the arXiv under “homotopy normal maps”).

    http://arxiv.org/pdf/1011.4708v7.pdf

    But I think “homotopy actions” have a better flexibility as they are maps of arbitrary simplicial spaces that “behave” like principal G-action in a Segal-like sense, i.e. some maps built from the diagram must be homotopy equivalences. Theorem 5.15 there shows that you don’t loose any homotopical information in this weaker form.

    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeMar 16th 2012

    The term “principal ∞\infty-bundle” subsumes what you call “homotopy action”.

    • CommentRowNumber15.
    • CommentAuthorMatanP
    • CommentTimeMar 16th 2012

    Maybe I’m missing something but the way I see it, there is a slight difference between principal ∞\infty-bundle and homotopy action in that the former is defined by specific (homotopy) fiber products, and the latter is just a map of simplicial spaces, in which some maps that one “cooks” from it make every level being equivalent to these specific homotopy fiber products.

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeMar 16th 2012

    One general abstract difference is that principality is an extra condition on an ∞\infty-action. But that is not the point of discussion here, I guess, so let’s just talke about ∞\infty-actions.

    Those can be defined abstractly in various way, for instance in terms of ∞\infty-operads or in many cases simply in terms of ∞\infty-fiber sequences.

    Then there are, in turn, various models for these notions, in terms of simplicial objects and model category structures etc. pp. The simplicial spaces that you have in mind are one out of many possible ways to model the objects in question.

    • CommentRowNumber17.
    • CommentAuthorMatanP
    • CommentTimeMar 16th 2012
    • (edited Mar 16th 2012)

    It seems to me that definition 1 (principal G-action) is completely analogous to the rigid case of a homotopy action, i.e. given a topological group G and a G-space X, the projection map Bar •(X,G)→B •GBar_\bullet(X,G)\to B_\bullet G is an example of a homotopy action of ΩBG\Omega BG on X. Theorem 5.15 essentially says that all homotopy actions are weakly equivalent to the case above. Perhaps homotopy action is not a good name (I was not aware of principal ∞\infty-bundles when I wrote it) but in light of the nLab entry, homotopy actions are a version of ∞\infty-principal bundles rather than ∞\infty-actions. Am I missing something here?

    • CommentRowNumber18.
    • CommentAuthorjim_stasheff
    • CommentTimeMar 17th 2012
    @ in light of the nLab entry, homotopy actions are a version of ∞-principal bundles rather than ∞-actions.

    or rather in the darkness of not having recalled what's in that entry, I'm worried about a deluge of terminology:
    In topology (simplicial sets would do), there is the classic notion of homotopy action meaning a(bx) homotopic to (ab)x
    with no higher homotopies. Not quite so ancient is oo-homotopy action (aka sh-acton) which for nice spaces A acting on X is equivalent to a strict action of \omega BA on X.
    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeMar 17th 2012
    • (edited Mar 21st 2012)

    homotopy actions are a version of ∞-principal bundles rather than ∞-actions.

    We call an action ρ:G×V→V\rho : G \times V \to V (homotopic or ordinary) “principal” if it satisfied the principality condition , meaning that the canonical morphism G×V→(ρ,p 1)V× XVG \times V \stackrel{(\rho, p_1)}{\to} V \times_X V is an equivalence.

    • CommentRowNumber20.
    • CommentAuthorMatanP
    • CommentTimeMar 19th 2012

    Jim: do you of a notion of a principal action of an A ∞A_\infty-space?

    • CommentRowNumber21.
    • CommentAuthorjim_stasheff
    • CommentTimeMar 19th 2012
    If you are asking if I know of such, sure
    Just take the usual definition of an $A_\infty$-space X
    and rewrite it for an action of X on the total space of a fibration
    X --> P --> B
    by putting p in P in the last slot and require that the action be fibrewise

    now to find a reference
    • CommentRowNumber22.
    • CommentAuthorMatanP
    • CommentTimeMar 19th 2012

    So just to be sure:

    If I have a homotopy fibration sequence ΩB→X→Y\Omega B\to X\to Y, then it is an “∞\infty-principal fibration” precisely when there is a map Y→BY\to B such that X→Y→BX\to Y\to B is a homotopy fibration sequence?

    • CommentRowNumber23.
    • CommentAuthorMatanP
    • CommentTimeMar 20th 2012

    ok. I added a short discussion after definition 1 on “homotopy actions”. The precise relation is still not completely clear to me but the diagramatic description is similar so there must be a connection.

    I hope this will initiate a discussion on the connection to the general definition.

    In particular, I think that the axiomatic description can be generalized to an (∞,1)(\infty,1)-topos.

    • CommentRowNumber24.
    • CommentAuthorjim_stasheff
    • CommentTimeMar 20th 2012
    @ Urs 19: We call an action ρ:G×V→V (homotopic or ordinary) "principal" if it satisfied the principality condition , meaning that the canonical morphism G×V→(ρ,p 1)G×G is an equivalence.

    Obvious typo, but even so, who are `we' and where does this occur in the lit? aned what kind of euivalence? or does that depend on (homotopic or ordinary)?
    • CommentRowNumber25.
    • CommentAuthorjim_stasheff
    • CommentTimeMar 20th 2012
    @Matan P 22: If I have a homotopy fibration sequence ΩB→X→Y, then it is an "∞-principal fibration" precisely when there is a map Y→B such that X→Y→B is a homotopy fibration sequence?

    yes, subject to the usual restrictions on the category cf. nice spaces

    @23 added where?
    • CommentRowNumber26.
    • CommentAuthorMatanP
    • CommentTimeMar 20th 2012

    @jim_stasheff 25: added at principal infinity-bundle

    • CommentRowNumber27.
    • CommentAuthorUrs
    • CommentTimeMar 20th 2012

    Hi Matan,

    I think the pointers to your section 5 would better be added to the entry associated infinity-bundle not to principal infinity-bundle, because you don’t consider the principality condition (at least not around your def. 5.1, which you are currently referring to in your addition to the nLab entry.)

    At associated infinity-bundle is recalled some standard material on fiber sequences and their interpretation as homotopy actions, together with references. A pretty comprehensive account is the book by Peter May there, from 1975, which builds on Jim’s very work from 1963. The recent article by Wendt mentioned there contains a useful summary, together with the useful observation that much of the classical theory happening in topological spaces / simplicial sets fairly straightforwardly generalizes to 1-localic ∞\infty-toposes.

    It seems to me that what you discuss in your section 5 is a restatement of some of these classical things with an emphasis on the model for the general theory that is provided by Segal spaces. You do cite May’s book, so I am sure that you are aware of this.

    But for me it causes the following confusion: I am not sure what the discussion here is about. It is evidently not about principality (and to Jim: the condition I mentioned is the standard definition of principality!) but all about fiber sequences aka “associated ∞\infty-bundles” in the (geometrically) discrete context, which has been well established for a few decades.

    • CommentRowNumber28.
    • CommentAuthorMatanP
    • CommentTimeMar 20th 2012

    Hi Urs,

    The issue of principality is the point where I get confused. It is not explicitly written in definition 1 but rather stated in proposition 1, where it takes a “relative” form of the principality condition you mentioned in @19, i.e. fiber product instead of product. Moreover, homotopy actions satisfy definition 1 and proposition 1 of principal infinity-bundle for the case of the (∞,1)(\infty,1)-topos of topological spaces so it made sense to me to put a discussion there; if the diagrams are the same, how can it be different?. I’m not claiming that h.actions are a brand new thing but rather a new description in Segal’s coordinate system of an older insight for higher relations in an “action”.

    • CommentRowNumber29.
    • CommentAuthorMatanP
    • CommentTimeMar 20th 2012

    another thing is that h. actions are defined abstractly for a loop space and a space so it doesn’t seem accurate to put it on associated infinity-bundle.

    • CommentRowNumber30.
    • CommentAuthorUrs
    • CommentTimeMar 21st 2012
    • (edited Mar 21st 2012)

    Hi Matan,

    I have moved the pointer to your work to the References-section at associated infinity-bundle, where, I think, it more properly belongs, and where readers who are after it have a better chance of finding it. If you insist that it needs to go at principal infinity-bundle, please add a pointer to your work in the References-section there. References should go in the References-section. If you want to add definitions etc. please do so in a way that fits into the existing text, or else open a new subsecftion for it.

    Concerning your confusion about principal actions:

    you are mixing up fibers with total spaces of principal bundles.

    If you have a fiber sequence

    A→B→BG A \to B \to \mathbf{B}G

    there are two ways to read it:

    1. you can regard BB as the base space, then B→BGB \to \mathbf{B}G classifies a GG-principal ∞\infty-bundle and the total space of that bundle is AA. So we tend to write P:=AP := A and have

      P → * ↓ ↓ B → BG. \array{ P &\to& * \\ \downarrow && \downarrow \\ B &\to& \mathbf{B}G } \,.

    2. You can regard BB as bundle over BG\mathbf{B}G. Then BB is the action groupoid of an action (“homtopy action”) of GG on AA, and you should think of the diagram as drawn like this

      A → B ↓ ↓ * → BG. \array{ A &\to& B \\ \downarrow && \downarrow \\ * &\to& \mathbf{B}G } \,.

      To compare to the above case: we are shifting the fiber sequence one slot to the left. The bundle B→BGB \to \mathbf{B}G will be associated to an Aut(A)Aut(A)-principal ∞\infty-bundle on BG\mathbf{B}G which is classified by a map BG→BAut(A)\mathbf{B}G \to \mathbf{B} Aut(A).

    Notice that the object BG\mathbf{B}G plays two orthogonal roles in both cases. In the first one it is the moduli stack that classifies a structure over BB. In the second it is itself the base space of a structure over it. Of course since in both cases there are maps into BG\mathbf{B}G, there is some common mathematics at work .

    To see this more clearly, maybe it helps to write out the continuation of our fiber sequences further to the left. The first one extends as

    ⋯→G→P→B→BG. \cdots \to G \to P \to B \to \mathbf{B}G \,.

    Looking at the right bit P→B→BGP \to B \to \mathbf{B}G we see a principal GG-bundle over BB classified by a map to BG\mathbf{B}G. But shifting one step to the left we see

    G→P→B G \to P \to B

    whis we may read now as exhibiting an action of ΩB\Omega B on GG (assuming that BB is connected). The holonomy-action.

    • CommentRowNumber31.
    • CommentAuthorUrs
    • CommentTimeMar 21st 2012
    • (edited Mar 21st 2012)

    Thinking about it, maybe I should improve on that lengthy reply by a shorter more precise statement:

    principality of an action is a notion with respect to a given chosen base. Every action happens to be principal over the base given by its action groupoid. But the default notion of an action is over the point. As such most actions are not principal.

    Here is a more concrete example to illustarte this: Let VV be a vector space equipped with the linear action of a group GG. Then this action is clearly in general not principal. But if you do regard VV as being a bundle over its own action orbifold V//GV//G, then as a bundle over that groupoidal base it does happen to become GG-principal. That’s a kind of exotic perspective on the action, though (albeit very useful) and we will be default instead regard the action over the point and say that the action of a group on a vector space is not principal.

    • CommentRowNumber32.
    • CommentAuthorMatanP
    • CommentTimeMar 21st 2012

    Hi Urs,

    Thank you for your detailed answer and intuition.

    The point I’m still confused about is the way the idea you describe in @30, @31 boils down to a definition.

    In the entry it says “Definition.1 (principal G-action): A principal action of G on an object P” which (by your comment) should mean a principal action over a point, but you then say that the base is X:=|P//G|X:=|P//G|.

    Perhaps this entire definition should be moved to associated infinity-bundle (since every GG-space P gives rise to the diagram that is described in the definition, namely Bar •(P,G)→Bar •(*,G)Bar_\bullet(P,G)\to Bar_\bullet(*,G)) or should be renamed, but as of now I can’t see how the discussion here is compatible with definition 1.

    • CommentRowNumber33.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    Okay, I have changed a little the wording of the definition:

    Let GG be a group object in the (∞,1)-topos H\mathbf{H}. A principal action of GG on a morphism (P→X)∈H(P \to X) \in \mathbf{H} is a groupoid object P//GP//G that sits over *//G*//G in that we have a morphism of simplicial diagrams Δ op→H\Delta^{op} \to \mathbf{H}

    ⋮ ⋮ P×G×G →(p 2,p 3) G×G ↓↓↓ ↓↓↓ P×G →p 2 G ↓↓ ↓↓ P → * \array{ \vdots && \vdots \\ P \times G \times G &\stackrel{(p_2, p_3)}{\to}& G \times G \\ \downarrow\downarrow\downarrow && \downarrow\downarrow\downarrow \\ P \times G &\stackrel{p_2}{\to}& G \\ \downarrow\downarrow && \downarrow\downarrow \\ P &\stackrel{}{\to}& {*} }

    in H\mathbf{H};

    and such that P→XP \to X exhibits the (∞,1)-colimit

    X≃lim →(P//G:Δ op→H) X \simeq \lim_\to (P//G : \Delta^{op} \to \mathbf{H})

    called the base space over which the action takes place.

    • CommentRowNumber34.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012

    Thinking about it: the kind of discussion we have here and your references should really first and foremost go to the entry infinity-representation, which needs to be expanded.

    • CommentRowNumber35.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    Great. In light of this change, perhaps a better name for definition 1 would be “relative principal GG-action”. I think there is still a problem in the definition. Let’s say we have a homotopy fibration sequence ΩB→P→X\Omega B \to P\to X together with a map X→BX\to B s.t. P→X→BP\to X\to B is a homotopy fibration sequence (by @25 it is called an ∞\infty-principal fibration). We know that G:=ΩBG:=\Omega B is a group object in the (∞,1)(\infty,1)-topos of topological spaces and we would like to say that this setting induces a principal GG-action of GG on (P→X)(P\to X). But formally speaking, we cannot produce even the first simplicial object in the diagram of definition 1 with G=ΩBG=\Omega B since the simplicial identities will not hold in it (this can be seen already when P=*P=* since concatenation in ΩX\Omega X is only associative up to homotopy).

    How can this inaccuracy be removed? In the case of spaces, we can try to rigidify G into a topological group in a compatible way with ΩB→P→X\Omega B \to P\to X but I don’t think we want to go there. Instead, we can construct a simplicial object A •A_\bullet via iterated (homotopy) fiber products of the map P→XP\to X. I.e., replace P→XP\to X by a fibration P′→XP'\to X and set A 0=P′A_0= P', A 1=P′× XP′A_1=P' \times_X P' and so on with honest face and degeneracies coming from this construction. However, we will not get the diagram in defintion 1 but rather a diagram in which level n is homotopy equivalent to P×G nP\times G^n. Similarly, we can take (homotopy) iterated fiber product of *→B*\to B and get a simplicial object B •B_\bullet in which level n is equivalent to G nG^n.

    Since we have a map between the (replacements of the) maps P→XP\to X and *→B*\to B (namely a square which I yet don’t know to draw in itex), we have a map of simplicial objects A •→B •A_\bullet\to B_\bullet. This simplicial map is very close to the one in definition 1 but if we want to be precise, we need to adapt the definition so that this map will satisfy it. One solution for this is to replace definition 1 by that of h. actions. There are probably other solutions and perhaps better ones. I don’t mean to brutally shove my stuff but I think it arises naturally from this situation.

    • CommentRowNumber36.
    • CommentAuthorjim_stasheff
    • CommentTimeMar 22nd 2012
    @27 URS:and to Jim: the condition I mentioned is the standard definition of principality!)

    in what community? and since when? and principality of ___?
    • CommentRowNumber37.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    sorry for multiple posts

    • CommentRowNumber38.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012

    …

    • CommentRowNumber39.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    we cannot produce even the first simplicial object in the diagram of definition 1 with G=ΩB since the simplicial identities will not hold in it (this can be seen already when P=* since concatenation in ΩX is only associative up to homotopy).

    No: this is a simplicial diagram in the ∞\infty-topos H\mathbf{H}. So it is an ∞\infty-functor Δ op→H\Delta^{op} \to \mathbf{H}. This means that all the simplicial identidies hold up to homotopies in H\mathbf{H}.

    • CommentRowNumber40.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012

    and since when?

    You may know the history better than I do. An early reference that I have right here is

    • J. Duskin, Simplicial methods and the interpretation of “triple” cohomology, Mem. Amer. Math. Soc. 3 (1975), issue 2, no. 163.

    See around def. 4.5.2.

    and principality of ___?

    I am talking about principal bundles. Standard definition.

    I am not sure, what is the issue? Asking that

    P×G→P× XP P \times G \to P \times_X P

    is an equivalence unwinds directly to the statement: the action of GG on the fibers over XX is free and transitive.

    • CommentRowNumber41.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    ok. But currently, in definition 1, where it says “simplicial diagram” it refers to simplicial object where only ordinary simplicial diagrams are considered.

    I hope all these small corrections are not too annoying but I got confused because of the initial formulation and other readers might too.

    • CommentRowNumber42.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    I have added to simplicial object the sentence

    More generally, a simplicial object in an (∞,1)-category is an (∞,1)-functor Δ op→C\Delta^{op} \to C.

    Have a look at section 6.1.2 Groupoid objects of Higher Topos Theory. The entry principal infinity-bundle is in effect just a small observation on top of the material discussed there, namely the observation that the ∞\infty-Giraud theorem directly gives the main content of principal bundle theory: since every groupoid object in an ∞\infty-topos is effective, the statement that that the quotient of the GG action is the base space

    P//G≃X P // G \simeq X

    is equivalent to the principality condition

    P×G≃P× XP. P \times G \simeq P \times_X P \,.

    That, and the observation that the principal ∞\infty-bundle classified by a morphism X→BGX \to \mathbf{B}G is simply its homotopy fiber.

    • CommentRowNumber43.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    thank you Urs for clarifying this point. In light of the description @35, wouldn’t you say that h. actions are closely related to definition 1? the way I understand it is that instead of describing infinity principal bundles in terms of (∞,1)(\infty,1)-functors, h.actions give a description in terms of ordinary simplicial objects that satisfy axioms which force them to look like the diagram in definition 1. For people that are not fully comfortable to do everything in the (∞,1)(\infty,1) framework (like me) it might be useful to have this alternative description.

    • CommentRowNumber44.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012

    As I said in #16,

    there are, in turn, various models for these notions, in terms of simplicial objects and model category structures etc. pp. The simplicial spaces that you have in mind are one out of many possible ways to model the objects in question.

    • CommentRowNumber45.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012

    wouldn’t you say that h. actions are closely related to definition 1?

    Sure, principal actions involve actions.

    I am not sure what you are worried about. If it is about having a pointer to your work added: it is currently listed in the entry on principal ∞\infty-bundles. Feel free to add it to the Reference-section of other entries. I think it belongs properly to infinity-representation and to homotopy fiber. (Weeks back I had already added it to normal subgroup). Best would be to add it there in the References-section and include in the main entry a discussion of what it is you do in the article, if that’s what you would like to have.

    • CommentRowNumber46.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012

    Sure, principal actions involve actions.

    lol. I meant that since definition 1 actually defines “relative principal action” which in turn arise from and gives rise to an action, then it is the same as h. action but phrased in terms of ∞\infty-functors instead of reduced Segal spaces.

    Definition 1 and the definition of h.action are both notions which are defined by by diagrams and these diagrams are essentially the same. Thus, the notions should be equivalent. I don’t care about having a pointer to my stuff, but rather to understand why another formulation which seems equivalent in my eyes is actually not equivalent (assuming this is what you’re claiming).

    • CommentRowNumber47.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    I meant that since definition 1 actually defines “relative principal action” which in turn arise from and gives rise to an action, then it is the same as h. action but phrased in terms of ∞-functors instead of reduced Segal spaces.

    Look at it for the ordinary 1-categorical case, to concentrate on the basic ideas: there is the notion of action of a group on something, and then there is the notion of principal bundle.

    The two notions are not eqivalent.

    A principal bundle involves an action, but it also involves extra stuff and extra properties.

    • CommentRowNumber48.
    • CommentAuthorMatanP
    • CommentTimeMar 22nd 2012

    Of course the notions in @47 are not equivalent. However, as I thought we agreed, definition 1 doesn’t define principal action but rather a principal action relative to a map P→XP\to X which becomes “usual” principal action only if XX is a point.

    • CommentRowNumber49.
    • CommentAuthorUrs
    • CommentTimeMar 22nd 2012
    • (edited Mar 22nd 2012)

    Definition 1 is the defintion of principal bundle, according to the name of the entry. If the GG there is an ordinary group and XX an ordinary manifold, then this is verbatim the traditional definition of principal bundle.

1 to 49 of 49

  1.