Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: anafunctors

Bottom of Page

1 to 33 of 33

  1.  
    • CommentRowNumber1.
    • CommentAuthorTodd_Trimble
    • CommentTimeJan 22nd 2010

    So sorry to have been away for a while. My computer has been having problems (and is still in the shop).

    I'm also sorry to whinge, but after looking at Mike's recent comment at the Café, I had a another look at the article anafunctor and surrounding material, and I'm a little bothered by the presentation. Mike says that ordinary functors should be called strict functors and anafunctors just 'functors', which seems to suggest that anafunctors are the better (or technically more advantageous) concept and so the world had better get used to them. Okay. So a sales pitch would seem to be in order, particularly for those for whom this concept is not yet second-nature. The nLab would be a good place to make that pitch.

    As I see it, one trouble with the article is that it makes the notion look harder than it should. I think I would find it easier to follow if the external definition started with the one-line definition that an anafunctor from C to D is a pair of functors 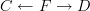C \leftarrow F \to D where the left arrow is a surjective (on objects) equivalence, i.e. surjective and fully faithful. I think most human readers of category theory would find this easier to follow or swallow than the nuts-and-bolts description given at the outset.

    A link is given to the stubby article on ananatural transformation. I hope someone will get around to improving that; the advice "I dunno, read Makkai or something" sounds very cavalier and not very kind or helpful (I have no idea where in all those gzipped documents I should look).

    I think it might help to have a section where an honest sample use of anafunctors is given, to exhibit its virtues over ordinary functors. I would rather not be referred to a long article for this; something more self-contained would be very nice and convenient for the reader.

    We are told that the first explicit formulation of the internal concept is given in Toby's paper. Fine, but where? I didn't see anything about 'ana' in the table of contents, and I didn't see an index either. Also, is Makkai's paper the standard go-to reference? I guess I could get off my lazy butt and gunzip all those documents and see what's inside, but it would be nice to know what lies ahead.

    The general complaint is that the article as it stands looks a bit forbidding. There is plenty of technical discussion (as in the section on questions of size), which is alright but may be scary to the newcomer; it would help to give a little something extra to the poor fellow, to make anafunctors seem more user-friendly (cf. sales pitch). Be gentle, without being cavalier.

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeJan 22nd 2010
    • (edited Jan 22nd 2010)

    Hey Todd!

    Good to see you again. I had been wondering where you are.

    Since you had been away, you may or may not have seen that Mike, Toby and I had recently had some discussion along these lines on the Cafe, starting around here.

    Concering the entry anafunctor: I have now done two things to it:

    • expanded considerably the Idea-section, trying to give a good idea of what's going on. This is meant as a proposal. Especially Toby should feel free to interfere and modify, if necessary.

    • expanded the references-section a bit.

    • CommentRowNumber3.
    • CommentAuthorTobyBartels
    • CommentTimeJan 22nd 2010

    Gee, it's been a while since I really worked on these entries.

    I did a bit with the definitions at anafunctor and ananatural transformation. I'll work on the Idea next.

    • CommentRowNumber4.
    • CommentAuthorMike Shulman
    • CommentTimeJan 22nd 2010

    Looking better, thanks for the suggestions Todd. I don't have time to work on this right now myself but I entirely agree the entry should be better.

    Actually, it's not actually clear to me that Makkai's original definition of anafunctors in terms of "specifications" is any use whatsoever; I always find it easier to think of spans.

    • CommentRowNumber5.
    • CommentAuthorTobyBartels
    • CommentTimeJan 22nd 2010

    In a concrete example, I usually think about specifications, but I also find the theory clearer with spans.

    • CommentRowNumber6.
    • CommentAuthorTobyBartels
    • CommentTimeJan 23rd 2010

    I added more helpful (hopefully) bits to anafunctor and ananatural transformation, but I haven't attacked the Idea section yet.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeJan 23rd 2010
    • (edited Jan 23rd 2010)

    Tim Porter kindly points out to me that Ronnie Brown kindly points out to him that Pradine kindly pointed out to him, in turn, that there is this reprint of an older article of Pradine's

    Morphisms between spaces of leaves viewed as fractions

    Looks like Pradines says "exactor" there for "anafunctor", at least in section 10. Only skimmed the article so far. Is hard to read quickly, lots and lots of nonstandard terminology.

    • CommentRowNumber8.
    • CommentAuthorTobyBartels
    • CommentTimeJan 23rd 2010

    If I understand the definition of exactor (Definition 7.1, but I had to chase a lot more down), it's a lifting property of individual smooth (strict) functors. The spans in Section 10 are pairs of exactors.

    There's something in that article, but you're right; it's hard to get through it all.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeJan 23rd 2010

    I see, okay.

    • CommentRowNumber10.
    • CommentAuthorMike Shulman
    • CommentTimeJan 24th 2011

    I added some comments to anafunctor about the relationship between anafunctors and representable profunctors.

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeJan 24th 2011

    Thanks, Mike. I had had similar thoughts when reading Benabou’s reply.

    Another thing that could be mentioned in reply to him is that the localization at acyclic isofibrations is easily seen to be well behaved: while we don’t immediately have a caluclus of fractions, we have for instance the structure of a category of fibrant objects and hence have explicit formulas for the homotopy category almost as in Gabriel-Zisman.

    • CommentRowNumber12.
    • CommentAuthorzskoda
    • CommentTimeJan 24th 2011

    How about the internal generalization ? I mean the internal profunctors have very well developed theory, while the bicategories of fractions are not worked out/known internally, at least as far as I know.

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeJan 24th 2011
    • (edited Jan 24th 2011)

    the internal profunctors have very well developed theory, while the bicategories of fractions are not worked out/known internally, at least as far as I know.

    It seems to me that David Roberts’ PhD thesis result gives a large class of setups for internal anafunctors for which a notion of internal profunctor does not even exist.

    Don’t we need considerably more ambient structure to say “internal profunctor”?

    • CommentRowNumber14.
    • CommentAuthorzskoda
    • CommentTimeJan 24th 2011

    Oh, I see, one does not need internal bicategories as well for organizing that, what I had in mind. Thanks for check of sanity :)

    • CommentRowNumber15.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 24th 2011

    @Urs - yes. we need well-behaved quotients to exist. By well-behaved I will be vague, but from general reasoning I believe that internal profunctors are much more closely linked to internal saturated anafunctors (=right principal bibundles). To define composition of saturated anafunctors one needs to form the equivalent of an associated bundle, whereby a quotient by an antidiagonal action is used. There is some condition about quotients and pullbacks interacting well, I think, but I haven’t written it down.

    • CommentRowNumber16.
    • CommentAuthorTobyBartels
    • CommentTimeJan 24th 2011

    There is some condition about quotients and pullbacks interacting well, I think, but I haven’t written it down.

    The condition that I used in my PhD thesis (and which holds in TopTop, DiffDiff, etc) was that quotients (of equivalence relations) are pullback-stable. Is this not good enough, or do you think that something even weaker will suffice? (I never spent much time worrying about saturated anafunctors, but I did worry about forming associated bundles.)

    • CommentRowNumber17.
    • CommentAuthorUrs
    • CommentTimeJan 24th 2011

    yes. we need well-behaved quotients to exist.

    Hm, maybe I am being dense. How do you make SetSet an internal category to, say, DiffDiff? What is a profunctor internal to DiffDiff?

    • CommentRowNumber18.
    • CommentAuthorTobyBartels
    • CommentTimeJan 24th 2011

    You certainly don’t define a profunctor in DiffDiff (say from CC to DD) to be a functor in DiffDiff from D op×CD^{op} \times C to SetSet, since (as you imply) SetSet is not an internal category in DiffDiff.

    Instead, you use the trick whereby a function (sic!) from a set AA to SetSet is replaced by an arbitrary function to AA, phrase the definition of functor to SetSet in elementary terms thus, and internalise.

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeJan 24th 2011
    • (edited Jan 24th 2011)

    So you identify the notion of profunctor externally with the fibration it classifies and then internalize that.

    This is a bit begging the question, because part of the point of internalizing is that concepts that are externally equivalent may become non-equivalent.

    Because if I allowed myself to switch the definition of profunctor externally, I can say:

    you use the trick whereby a representable profunctor is a equivalently an anafuncor, and then internalise.

    Whereby we have proven that internal anafunctors are equivalent to internal representable profunctors. QED.

    • CommentRowNumber20.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 24th 2011
    • (edited Jan 24th 2011)

    (cross-over there. I wrote this before Urs’ comment preceeding mine)

    @Urs, you use the equivalence between functors F:C→SetF:C \to Set and discrete (op)fibrations ∫F→C\int F \to C. Discrete (op)fibrations can be internalised without difficulty. In Makkai’s paper he has a throwaway remark that anafunctors X←X[P]→fYX \leftarrow X[P] \stackrel{f}{\to} Y between categories X,YX,Y are saturated precisely when the induced functor core(X[P])→core(X×Y)core(X[P]) \to core(X\times Y) is a discrete opfibration. This is the case when

    X 1 iso× X 0 2P 2→(X 1×Y 1) iso× X 0×Y 0P X_1^{iso} \times_{X_0^2} P^2 \to (X_1 \times Y_1)^{iso} \times_{X_0\times Y_0} P

    defined by

    (a;p 1,p 2)↦(a,f(a;p 1,p 2);p 2) (a;p_1,p_2) \mapsto (a,f(a;p_1,p_2);p_2)

    is an isomorphism. Here P→X 0P \to X_0 is a cover, of the sort you want (a surjective submersion, in Diff, or a local section admitting map, in Top, for example. Or you could take a surjective group homomorphism and you recover (essentially) butterflies between crossed modules). It is a consequence of this definition that PP is a right-principal bibundle (and you can go back again).

    Composing saturated anafunctors is a bit more tricky. You need to compose them as anafunctors, and then saturate - and this is where the subtlety lies. I think requiring that pullbacks preserve quotients of equivalence relations is enough for composing saturated anafunctors, but then proving that composition thus defined is functorial on hom-categories is another question. My notes break off at this point, and I went onto something else, so I can’t remember what I needed. I may have been over-complicating things, conflating the proof that saturated anafunctors form a bicategory with the proof (?) that saturated anafunctors between groupoids and bibundles between groupoids give equivalent bicategories.

    (You can see where the associated bundle operation comes in: Given a principal Y-bundle on X, and a saturated anafunctor Y→ZY \to Z, you need to form the associated principal ZZ-bundle on X.)

    • CommentRowNumber21.
    • CommentAuthorTobyBartels
    • CommentTimeJan 25th 2011

    @ Urs

    you use the trick whereby a representable profunctor is a equivalently an anafuncor, and then internalise.

    This doesn’t internalise profunctors in general, so of course there is no useful theorem.

    But if you have two classically equivalent definitions for a concept that you wish to internalise, you don’t force yourself to use whichever definition is most common in the textbooks; you use whichever definition works best. And mine works obviously better than yours, since we don’t even know how to write yours down!

    As David points out, it’s not even that ugly (which I had forgotten).

    • CommentRowNumber22.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 25th 2011

    @Urs #7

    What Pradines considers are essentially Hilsum-Skandalis maps aka bibundles aka saturated anafunctors. Unfortunately that paper is written in Ehresmann-style language, which very few people speak now. But other than that it is a good paper, and prefigures a bunch of stuff that is common now among Lie groupoid researchers.

    • CommentRowNumber23.
    • CommentAuthorUrs
    • CommentTimeJan 25th 2011
    • (edited Jan 25th 2011)

    Toby, David,

    you don’t have to convince me that this is a useful concept, I know and appreciate these constructions.

    On the contrary, what I doubted was Jean Benaubou’s attitude on the CatTheory mailing list that there is no point in the concept of anafunctor because there is already the concept of a functor valued in representable presheaves. In that discussion “profunctor” meant specifically that.

    We all seem to agree fine that for purposes of internalization, this is not a useful concept.

    • CommentRowNumber24.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 25th 2011

    Just wanting to get stuff written down. I really really need to labify my notes on saturated anafunctors…

    • CommentRowNumber25.
    • CommentAuthorzskoda
    • CommentTimeJan 25th 2011
    • (edited Jan 25th 2011)

    On the contrary, what I doubted was Jean Benaubou’s attitude on the CatTheory mailing list

    I needed to do some software installation for a colleague and tonight I watch the ski world cup so I can not delve into these, but my impression is that both profunctors and anafunctors have generalized versions which only partially overlap.

    • CommentRowNumber26.
    • CommentAuthorTobyBartels
    • CommentTimeJan 25th 2011

    I didn’t see anything in Jean Bénabou’s posts to suggest that he wouldn’t know how to internalise the definition of profunctor.

    • CommentRowNumber27.
    • CommentAuthorUrs
    • CommentTimeJan 25th 2011
    • (edited Jan 25th 2011)

    I didn’t see anything in Jean Bénabou’s posts to suggest that he wouldn’t know how to internalise the definition of profunctor.

    Since “the internalization” of the notion of profunctor in this sense is really the internalization of the spans associated to them, and since these are effectively the corresponding anafunctors in the representable case, why do you think he is objecting to the use of anafunctors then?

    (This is not a rethorical question. I’d really like to know.)

    • CommentRowNumber28.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 25th 2011

    @Zoran - that is probably about right. One one hand you have non-representable distributors, and on the other you have anafunctors in categories without quotients (or just non-saturated anafunctors).

    @Urs, I really don’t know. From what I know of him, Jean Benabou has great consideration for historical precedence, and is not one to work in a revisionist sense.

    • CommentRowNumber29.
    • CommentAuthorTobyBartels
    • CommentTimeJan 25th 2011

    I can’t see too well into another person’s mind, but I think that part of Bénabou’s gripe is that people seemed to be ignoring his established work in “distributeurs” for some other junk that his earlier work actually subsumes. (Mike neglected to even mention the connection! among all of the great things that he did mention.) Surely you are not suggesting that Bénabou is complaining that anafunctors are bad because they can be internalised while profunctors can’t! I really don’t see how else one would internalise a profunctor, even in a topos, except by something along the lines that I suggested.

    Note also that redefining profunctors as certain spans is the same thing even up to isomorphism, not merely up to equivalence, which is probably important to Bénabou, given his hatred of the hatred of evil. So it really is the same thing, even from a perfectly strict (albeit not actually material) standard.

    • CommentRowNumber30.
    • CommentAuthorMike Shulman
    • CommentTimeJan 26th 2011

    It sounded to me, in his last email, like he was saying that if anafunctors are the same as representable distributors, and we also have non-representable distributors with lots of important applications, why should we introduce a new thing called “anafunctor” instead of using the existing “representable distributors” which have better connections to other useful things? Hence why I tried to explain some of the uses of the anafunctor viewpoint that distributors don’t have.

    “the internalization” of the notion of profunctor in this sense is really the internalization of the spans associated to them

    I think that’s a somewhat misleading thing to say. Profunctors can be defined in many equivalent ways; it just so happens that some of those definitions can be internalized more easily than others. I don’t think it’s necessarily justified to say that one of those definitions is only about “the spans associated to” a profunctor rather than being an equally valid definition of a profunctor.

    • CommentRowNumber31.
    • CommentAuthorUrs
    • CommentTimeJan 26th 2011

    Hi guys, this is my last comment here, as I feel we are wasting time with disagreeing over nothing while agreeing over everything.

    You all keep telling me that the span-version is an equivalent way to talk about profunctors and that therefore there is no point in making a distinction. Did I ever doubt this? No. This “discussion” started with Benabou making a distinction and me pointing out that if one makes a distinction, then internalization becomes problematic. After which you started telling me how to internalize profunctors by not making that distinction.

    If it’s me who is not expressing myself properly, please accept my apologies. But let’s leave it at that then or turn to a more constructive discussion.

    (No offense intendend, I hope you can see where I am coming from. If not, anyway, let’s use our time on other things.)

    • CommentRowNumber32.
    • CommentAuthorTobyBartels
    • CommentTimeJan 26th 2011

    I wrote (#29):

    Note also that redefining profunctors as certain spans is the same thing even up to isomorphism, not merely up to equivalence

    Actually, this isn’t true. I was thinking that the canonical equivalence Fun(A,Set)≃Set/AFun(A,Set) \simeq Set/A is an isomorphism (in a framework such as ZFCZFC where this even makes sense), but it’s not; I was making the old mistake of conflating unions with disjoint unions. It’s a monadic adjoint equivalence.

    This “discussion” started with Benabou making a distinction [between distributors and their span-versions].

    I don’t think that this is accurate, which is why I’ve been disagreeing with you. (I also thought at one point that you genuinely didn’t know how to internalise distributors, but that was my mistake.)

    But if our only disagreement is over what Bénabou meant, then I’ll agree that we’re wasting time.

    • CommentRowNumber33.
    • CommentAuthorMike Shulman
    • CommentTimeJan 26th 2011

    Yes, let’s stop. (-:

1 to 33 of 33

  1.