nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorAndrew Stacey
- CommentTimeJan 22nd 2010
Started smooth loop space, initially just a stub. Partly to contain some bits of general theory relating to which smooth paths do I use (davidroberts) and partly to start transferring some notes on the differential topology of loop spaces over to the nLab.
In looking for somewhere to graft it on to the current nLab tree, I encountered loop space object. It seemed to me that the smooth loop space is not a loop space object, so I commented as such (thus also creating the link to smooth loop space which was my real intent). Someone who knows these things better than I do should check this.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
- (edited Jan 22nd 2010)
The smooth loop space is the loop space object of the smooth path groupoid
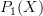 , for instance!
, for instance! -
- CommentRowNumber3.
- CommentAuthorAndrew Stacey
- CommentTimeJan 22nd 2010
I suspect that there's a diagram that would explain that remark perfectly. Could you add it somewhere for me?
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
oh, sorry, I didn't mean to be cryptic, I thought this was clear to you
I'll add a description now...
-
- CommentRowNumber5.
- CommentAuthorAndrew Stacey
- CommentTimeJan 22nd 2010
Thanks.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
okay, I wrote something into a new section
As a loop space object of the smooth path groupoid
Probably too verbose. And likely still cryptic. But have a look and let me know what you think.
-
- CommentRowNumber7.
- CommentAuthorAndrew Stacey
- CommentTimeJan 22nd 2010
This is what I like about the nLab. I create a page, more or less as a bookmark, and lo and behold, it gets filled with interesting stuff!
Too late now to grok it completely, but looks promising. I'll get back to you on that.
(Incidentally, Chris S-P has just asked about loop spaces over on mathoverflow. Bit of an open-goal for me, but I mentioned this page in my answer partly as motivation to me to get on with adding to it. Time I did some mathematics in the lab rather than just maintenance!)
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
This is what I like about the nLab. I create a page, more or less as a bookmark, and lo and behold, it gets filled with interesting stuff!
Yes, I like that, too! And I am looking forward to more interaction on technical matters with you in particular. I was getting worried that you having to take care of all our software admin needs kept you from enjoying actually using the Lab.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
polished a bit more and then
added a section Details on the smooth structure using an MO contribution (as indicated there)
added a very stubby References-section
-
- CommentRowNumber10.
- CommentAuthorAndrew Stacey
- CommentTimeJan 25th 2010
Found some junk online somewhere about the actual structure of the charts for a loop space (when thinking of it as a Frechet manifold) so copied it across almost verbatim.
(I've also sent it back in time so that if the original author ever notices that we've pinched his stuff then we can sue him for plagiarism.)
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
I have reorganized two of the sections at smooth loop space: I made the discussion of the Fréchet manifold structure appear before that of its relation to the diffeology, and gave the latter a more descriptive title.
Then I added one more brief Properties-section: G-Structures on smooth loop spaces with pointers to relevant articles.
I have also edited the Idea-section a bit. I think now it flows more naturally. But check if you disagree.
-
- CommentRowNumber12.
- CommentAuthorAndrew Stacey
- CommentTimeNov 7th 2012
That opening sentence has got to be a candidate for the highest density of the word “smooth” in a single sentence! I counted eight.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
Shall I change it or are you going to?
-
- CommentRowNumber14.
- CommentAuthorAndrew Stacey
- CommentTimeNov 7th 2012
Sorry - took a break for lunch! I’ll change it.
-
- CommentRowNumber15.
- CommentAuthorAndrew Stacey
- CommentTimeNov 7th 2012
I’ve had a go. You might think I’ve gone too far in the other direction.
I’m not happy about using the term “smooth space” for smooth space without qualification. The whole point of Comparative Smootheology is that there are a variety of categories that could lay claim to that of “smooth space” and so to designate one as seemingly the category of smooth spaces is a little confusing to say the least. Particularly on a page such as smooth loop space where the various different natures of a smooth loop space are gone into in quite some detail (thinking of the manifold structure in particular).
I liked the paragraph about how the smooth loop space might turn out to be nicer than expected (if one restricts to a subcategory) so I tried to keep that whilst remaining agnostic to the surrounding category.
In fact, isn’t this actually a theorem rather than a simple statement of fact? That if we take the inclusion Man→SSp (where SSp is (almost) any category of smooth spaces and Man is smooth finite dimensional manifolds) then the functor L:Man→SSp defined by L(M)=SSp(S1,M) factors through the inclusion Frechet→SSp. After all, there doesn’t seem to me to be any particular reason why the inclusions between these various categories should respect cartesian closedness - especially since the category of Frechet manifolds isn’t cartesian closed (I would presume that for some of the categories of gen.sm.sp then it follows from some of the adjunctions in Comparative Smootheology, but I guess that the adjunction has to be the right way around).
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
Okay, looks good.
there are a variety of categories that could lay claim to that of “smooth space”
Which one that you like is not a full subcategory of Sh(CartSp)?
-
- CommentRowNumber17.
- CommentAuthorAndrew Stacey
- CommentTimeNov 7th 2012
Taking the question seriously then Chen’s first definitions wouldn’t work. Nor, I think (but would need to check) do the “maps out” versions work. I’d also guess that any that had underlying topological space instead of set might prove troublesome. Moreover, it’s a bit naive to say “everything’s a subcategory of Sh(CartSp) so we may as well work there” since various constructions are different in the different subcategories (my point about cartesian closedness, above).
It’s partly that the term “smooth space” is so generic that to pin it down to a particular category feels bad. To be clear, I think it is fine for an individual page (or even group of pages) to state: “Here we will use “smooth space” to mean an object of 𝒮”. I don’t think it is fine to make this declaration across the entire nLab. I think that the page smooth space is about right on this (with the exception of the ambiguity of the word “here”), but when taken out of context (ie when linked from another page) then it could be clearer what the page smooth space is really about.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
- (edited Nov 7th 2012)
I think (but would need to check) […] I’d also guess […]
Somebody should check!
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
I’d also guess that any that had underlying topological space instead of set might prove troublesome.
Convenient vector spaces form a full subategory of the smooth topos. Which definitions are you worried about?
-
- CommentRowNumber20.
- CommentAuthorAndrew Stacey
- CommentTimeNov 7th 2012
Some definitions (Smith, Sikorski, early Chen) were of the form “A smooth space is a topological space + some stuff”. These wouldn’t embed in Sh(CartSp) because you could have the same smooth functions from Euclidean spaces but different (compatible) topologies. So the topology is not determined by the smooth structure.
If you want an all-encompassing category then you want to take the category built as follows:
T is all conceivable test objects. So that’s everything where we are absolutely certain what the smooth functions are. In Comparative Smootheology I had some description of this as taking all subsets of Euclidean spaces with a particular property that made them locally look like convex subsets of Euclidean space.
Objects of S are then triples (I,O,c) where I:T→Set and Oop:T→Set are functors and c:I×O→Hom is a natural transformation of bifunctors (probably some conditions here to ensure that c behaves like composition).
Morphisms are pairs of natural transformations that make a certain natural diagram commute.
Then that will encompass absolutely everything that anyone has ever proposed, I think.
However, I don’t recommend it.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
If you want an all-encompassing category
No, I don’t. I just want Sh(CartSp), nothing else. I just think that most of what you actually care about is in there.
-
- CommentRowNumber22.
- CommentAuthorAndrew Stacey
- CommentTimeNov 7th 2012
I didn’t think that you did!
However, whilst I agree that most of what I care about is in there, there’s also a lot that I don’t care for. And there are others who might like categories that have stuff that isn’t in there. So I think that “smooth space” should be reserved as a generic term that needs a context to make it precise because that reflects what happens in the literature.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeNov 7th 2012
Actually, I have another complaint about the term “smooth space”, maybe we can agree for different reasons: the term does not mesh well with smooth infinity-groupoid, because of the common ambiguity of “space”.
So at geometry of physics I started saying “smooth 0-type” instead (or rather, at the moment I say there “smooth space” but denote the category of them as “Smooth0Type”). In that vein, I should eventually rename smooth ∞-groupoids to “smooth types”.
On the other hand, that has its problems, too. And it will be loads of work to change it all…
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMay 27th 2013
I have added at smooth loop space in the References-section a pointer to
- Richard Melrose, Analysis on loop spaces, Lecture notes, 2013 (pdf)
-
- CommentRowNumber25.
- CommentAuthorAndrew Stacey
- CommentTimeMay 27th 2013
Can you explain why you’ve added that link? The notes are quite sketchy and I’ve not seen (on a skim read) anything that isn’t already referred to in other references.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMay 27th 2013
- (edited May 27th 2013)
I have added it because Melrose talked about it at IHES today, and I hadn’t know that he has notes on this and want to remember the link. But, yeah, they are sketchy. I have added to the entry now a qualification “There are also these sketchy notes…” Feel free to add further comments. But I’d find it useful to keep the link around.
1 to 26 of 26