nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 24th 2010
stub for free loop space object
this is what should be mentioned in that section I added to smooth loop space, instead of the based loop space object notion. Maybe later.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 25th 2010
considerably exapnded free loop space object. Additions include:
an Idea-section
unwrapping of the intrinsic definition in terms of homotopy pullbacks
discussion of how the fiber over a point is indeed the based loop space object
a pedestrian walk in full detail through the computation that
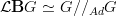
-
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 27th 2010
I'd like to add something on the categorical circle action on defined. Since do not feel too sure on my understanding of it, let me sketch it here: if it will turn out not to be too wrong, I'll take care of polishing it a bit and including it in free loop space object.
a point in is (by definition of limit) the same thing as a map from the homotopy pushout to . the latter is a model for the homotopy pushout of , i.e., of . Since in all these objects are represented by , it is reasonable to call them the circle object of the infinity-category , and maybe it's worth denoting it by . in the end, one should have an identification of with (when is closed); since acts on itself, it acts on and so on . -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
Yes, thanks, that's a very good point.
When I worked on the entry I had meant to add something on how the free loop space given by the pullback is also the mapping space form ta circle object, but then didn't get around doing this.
Notice that in the references that I listed, notably the Toen-Vezzosi one, this is the preferred perspective for most aspects.
The advatage of the homotopy-pullback definition is that that's the one that explains why cohomology of such loop space objects is really Hochschild cohomology of the underlying space.
We should certainly add this, yes. What you write seems to be entirely correct to me, yes. I would feel inclined to add as another "walked exercise" the explcit computation of that homotopy pushout,but I can do that later, after you added that.
-
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
added "categorical circle action" subsection. as far as concerns the walked exercise in pushouts, maybe it's worth creating an independent entry circle objects and to link to it from free loop space objects
edit: by the way, Anonymous Coward in the last revision of free loop space objects it's me, I forgot signing from this computer -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 27th 2010
also, following Toen and Vezzosi, we should add something on Chern classes from loop spaces. this directly points to 1-dimensional TQFT. I'll try to add something in this direction later today.
also, an iterated loop space construction should have some intersection with elliptic cohomology (in the spirit of Witten's Dirac index on loop spaces). later.. -
- CommentRowNumber7.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 27th 2010
- (edited Jan 28th 2010)
the argument relating loop spaces with characteristic classes of vector bundles should go as follows:
i) by universal property of pullback, is functorial
ii) given a linear representation , the trace of is invariant by conjugation, so it defnes a map , and so a map
iii) a principal -bundle on is a map , so it induces a map . by composition, one gets a map i.e., an element of the Hochshild cohomology of with coefficients in .
iv) now one has to go from Hochshild cohomology to ordinary cohomology (to be continued.. (I have to think on this))
by the way, when one sees that any linear representation of induces a real cohomology class of , and this way one should recover the classical definition of characteristic classes.
edit: since trace of the direct sum is the sum of traces and trace of tensor product is the product of traces, the above construction should give a ring homomorphism from the representaton ring of to the real cohomology of .
edit: I removed a few 's in the wrong place, see Urs' post below. -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
Thanks a lot! Very nice.
Let me just get something else out of the way, then I'll look into this. Thanks for pushing the bit on Chern classes, in particular.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
okay, I have now found a minute and expanded what you wrote a little,
for instance I mentioned presheaves and the Yoneda lemma for saying what we mean by
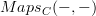 as an object in C when C isn't assumed to be closed.
as an object in C when C isn't assumed to be closed.Please have a look and see if you agree with what I did-
-
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
I agree, and also fixed a few typos :-)
as soon as I'll have a clear picture of Hochshild cohomology --> real cohomology (the circle action should be relevant here) I'll add the characteristic classes discussion sketched above after the example. -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
concering characteristic classes:
I am wondering about the step where you say from a representation of G you get a morphism
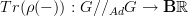 .
.I'd think from the rep you get a class function
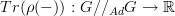
(i.e, without the
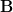 ): a group element
): a group element 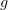 is an object in
is an object in 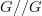 and is sent to
and is sent to 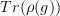 and this assignment is constant on morphisms
and this assignment is constant on morphisms 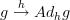 of
of  .
. -
- CommentRowNumber12.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
This reminds me of a gap in nlab: we should try to explain to ourselves the general nonsense of traces in cohomology theory (for example, traces in the setup of fibered categories). There are several definitions of a general trace in cohomological setup, one should look into old papers of Tsygan, Beilinson, Feigin. Most useful these general definitions are in cyclic cohomology.
I am not talking the facet which is in current entry trace. I mean the situation without duals. See for example Kaledin's treatment in tokyo6.pdf, see also tokyo5.pdf where the Hochschild cohomology is described as a derived functor of a trace functor.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
So I think this is one of the points of the Ben-Zvi/Franci/Nadler paper, that Hochschild homology of a monoid in an oo-category is to be identified with its trace (oo-trace/ derived trace). And Hochschild cohomolog with the center (oo-center, derived center).
-
- CommentRowNumber14.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 28th 2010
@Urs: concerning characteristic classes: yes, you're right, trace gives you a map to , not to . but luckily this is wat we want: one ends up with an element of and it is this to be Hochshild cohomology with real coeficients.
now I'll edit my post above so thta future readers will not be confused. -
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
one ends up with an element of
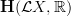 and it is this to be Hochshild cohomology with real coeficients.
and it is this to be Hochshild cohomology with real coeficients.Let's discuss this, I am not entirely sure I understand this in full detail. What I understand -- maybe ironically -- is the more high-brow perpective where we consider
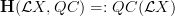 , the oo-category of quasicoherent sheaves on
, the oo-category of quasicoherent sheaves on 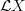 and identify this with the Hochschild homology/trace of the monoidal oo-category
and identify this with the Hochschild homology/trace of the monoidal oo-category 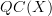 .
.Now when instead we just hom into
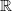 we'll get something very small. Can we think a moment about what that actually is? Is that the degree 0 Hochschild homology of the ring
we'll get something very small. Can we think a moment about what that actually is? Is that the degree 0 Hochschild homology of the ring 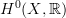 or real (singular) degree 0- cohomology of X?
or real (singular) degree 0- cohomology of X? -
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Trace functor were systematically used to define Hochschild cohomology and cyclic cohomology in a huge and deep paper Additive K-theory by Tsygan and Feigin in 1980-s (LNM 1289, editor Manin, pp 67-209, seminar 1984-1986 in Moscow). | do not think that this is confined to symmetric situations like infinity-categories. The fact that cyclic cohomology has to do with center has been explained to me by Bressler in Arizona 2002 and he gave a related talk in Stockholm 2004. One of his motivations is a remarkable lemma due Goodwillie from 1990s which says that the cyclic nerve of an inertia groupoid is the same as the cyclic envelope of the usual simplicial nerve of the original groupoid. This has been the reason for me to conjecture in Dec 2002 the theorem which has been independently discovered and published by Hinich on the induced phenomenon at the level of categories of sheaves. This paper of Hinich in turn has been much of a motivation to BenZvi Nadler's paper. But I am not happy with the outcome because some of the initial ideas (I skipped many side tracks including the relation to the crepant resolution conjecture , to coefficients in Hopf cyclic cohomology of Connes/Moscovici and relation to Drinfeld double, and recent Rosenberg's universal cyclic cohomology) are NOT yet realized.
Again one can have different traces, they are PART of the data. Ben Zvi and Nadler take just one particular trace which comes up in their situation.
-
- CommentRowNumber17.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
<div> <blockquote><br/>Now when instead we just hom into we'll get something very small. Can we think a moment about what that actually is?<br/></blockquote><br/><br/>my idea was that this should be the function algebra on the loop space. according to the final remarks in <a href="https://ncatlab.org/nlab/show/Hochschild+cohomology">Hochschild cohomology</a>, in nice situations this should be the algebra of differential forms on , but without the differential. the differential should come from the circle action. so the construction of characteristic classes could go nicely to an end if the function on one builds from the trace of a representation is -equivariant. this should be the circle-action analogue of being a closed differential form and so taking its de Rham cohomology class we would have a real cohomology element.<br/><br/>edit: moreover, taking , the compatibility of trace with direct sums and tensor products of vector bundles over makes the above construction a ring homomorphism , hence a very good candidate to being te Chern character. </div> -
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
@Zoran,
okay, I still need to look into this. Certainyl the relation of Hochschild cohomology to cohomology of loop spaces is what realizes that trace geometrically (the closing of the loop!)
@ Domenico: I guess you are quite right. This sounds good. Let me just think about "ordinary" function algebras on derived loop spaces a bit more. I find it easy still at the moment to get myself mixed up about the fully derived context. The very fact that a plain space has a nontrivial derived loop space is something kind of remarkable. While I understand it, I need to familiarize myself with that more.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
quick "Idea"-remark at cyclic cohomology
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
Domenico,
of course you are right. The statement is for instance on p. 4 of Loop spaces and langlands paramerters. (It will certainly be a much older statement, but that happens to b the reference I have handy.)
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Domenico,
so that's a very nice story about the Chern character that you point out there. Will you write a note on it in the Lab?
Now I am wondering if we can use this trick to define the Chern character for general objects A, not just for
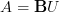 and alike.
and alike. -
- CommentRowNumber22.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
<div> <blockquote>Certainly the relation of Hochschild cohomology to cohomology of loop spaces is what realizes that trace geometrically (the closing of the loop!)<br/></blockquote><br/><br/>and this screams 1-!!!! </div> -
- CommentRowNumber23.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 28th 2010
Urs,
sure I'll add the Chern character note to loop space object. this will happen almost surely during the week-end (at the moment I should be correcting my students' linear algebra exams..) -
- CommentRowNumber24.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
okay, I still need to look into this. Certainyl the relation of Hochschild cohomology to cohomology of loop spaces is what realizes that trace geometrically (the closing of the loop!)
This is a special setup, I had remarked that nlab should also have general nonsense which is widely applicable. In algebra there rae many situations which do not fit into this setup, with Hochschild and cyclic cohomology of monoids in (possibly non-symmetric) monoidal categories equipped with a trace functor (not THE trace functor, but any, and there are general nonsense definitions and approaches to what that means, and considering derived functors of such, considered in the literature of last 20 years).
Connes has inrtoduced the cyclic object A sharp in algebras starting with an algebra A, similarly one starts with a monoidal category C and constructs a categroficiation: cyclic object C sharp in 2-category of categories, i.e. a cofibred category over the Connes' category of cycles. One should express traces in terms of cofibered or fibered categories like that example.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
okay, where should i start looking for general trace functors? It seems I have trouble finding an online copy of "Additive K-theory". Is there some newer review?
-
- CommentRowNumber26.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
I have the scan if you want, but more important are the contemporary ncg lectures of Kaledin and his arxiv paper cited at cyclic cohomology. This insight into traces explains appearance of Yang?Baxter braidings in coefficienst for Hop-cyclic like in works of Kaygun; the construction of simplicial objects from comonads in my preprint and more general construction of Bohm and Stefan having both as special cases. Maszczyk has geometric understanding into another direction.
-
- CommentRowNumber27.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 30th 2010
added the discussion on chern character to free loop space object -
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
Thanks!
I have expanded this slightly now --nothing substantial, just added more references and tried to amplify some points a bit more.
Check if you can agree with what I did.
Eventually, we want more details here on derived function algebras in general and how exactly differential forms are functions on derived loop space objects....
-
- CommentRowNumber29.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
absolutely agree. maybe we could add a few details on the S^1-invariance of the characteristic class (I'll add them, just tell me if you agree)
i) if is a morphism in C, the induced morphism is S^1-equivariant
ii) the S^1-action on is (this should be said better. what I mean is that in groupoids the action of on is .
hence the Ad-invariance of the trace makes the characteristic class S^1-equivariant. -
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
can we think about this for a second? I suppose you are right, but help me with the following:
we may think
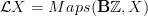 . On this acts
. On this acts 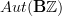 whose objects are those functors coming from automorphisms of the additive group
whose objects are those functors coming from automorphisms of the additive group 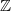 given by multiplication with some fixed integer
given by multiplication with some fixed integer 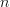 .
.From this I seem to get that the action of
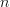 on a morphism
on a morphism 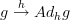 in
in 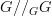 produces
produces 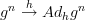 .
.So what's wrong about this reasoning?
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
oh, maybe I see: we are probably just (or in particular) looking at the inner automorphisms of
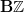 , i.e. those automorphisms that are connected by a natural transformation to the identity automorphisms.
, i.e. those automorphisms that are connected by a natural transformation to the identity automorphisms.These must al be the identity automorphisms themselves (since
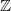 is abelian) but there is
is abelian) but there is 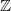 -worth of transformations relating the trivial automorphism of
-worth of transformations relating the trivial automorphism of 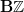 to itself. And these do act by conjugation.
to itself. And these do act by conjugation. -
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
right, that's probably it: we know that as we pass to the homology of the circle, which is the ring of dual numbers, we should be seeing the automorphisms of the odd line here: there is an even one, corresponding to a true automorphism of
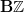 which is responsible for the N-grading, and there is an odd one, corresponding to a transformation of automorphisms, which is responsible for the de Rham differential.
which is responsible for the N-grading, and there is an odd one, corresponding to a transformation of automorphisms, which is responsible for the de Rham differential. -
- CommentRowNumber33.
- CommentAuthorzskoda
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
This reminds me of
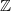 worth of automorphism of object
worth of automorphism of object ![[0] [0]](/extensions/vLaTeX/cache/latex_164f6be03ccb284b3efa092ceeb2a907.png) in a particular model of Connes' cyclic category description of which I wrote in category of cycles and which we had some time an argument if it is correct.
in a particular model of Connes' cyclic category description of which I wrote in category of cycles and which we had some time an argument if it is correct. -
- CommentRowNumber34.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
yes, we should be consideing only the categorical action of on itself, and not the action of .
@Urs: to be honest, to decide which the action of on should have been I just tried to guess a reasonable answer, keeping in mind the requirement that should have been invariant (which rules out your first guess) -
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
yes, we should be consideing only the categorical action of
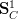 on itself,
on itself,Could you say very explicitly what you mean by this? Just so we are sure that we are on the same page?
I was thinking that my above comment was indeed on the right track (though I don't follow this track under full steam at the moment, as I need to concentrate on something else).
Recall from page 4 of Ben-Zvi/Nadler's "Loop spaces and Langlands parameters" that automorphisms of the odd line are supposed to be a rational approximation to
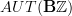 . That should make sense: the former is graded, the latter is a 2-group. The even degree part of the former should correspond to the objects of the latter, the odd degree part of the former to the morphisms of the latter.
. That should make sense: the former is graded, the latter is a 2-group. The even degree part of the former should correspond to the objects of the latter, the odd degree part of the former to the morphisms of the latter.It is the odd degree part of
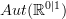 that gives the de Rham differential on
that gives the de Rham differential on 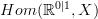 . Accordingly it should be the transformations in
. Accordingly it should be the transformations in 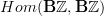 that are responsible for the "circle action by conjugation". And I think they do. I'll draw the corresponding diagram into the entry in a minute.
that are responsible for the "circle action by conjugation". And I think they do. I'll draw the corresponding diagram into the entry in a minute. -
- CommentRowNumber36.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
well, I only see this clearly in Top. but there it is quite clear that acts on itself by rotations, and that this action on becomes a rotation of the loop, which essentially moves forward or bacwards the starting point of the loop. when taking holonomy along the loop, rotating the loop changes the group element by conjugation, so its trace is left invariant.
but, let's try to see whether our two viewpoints can nicely fit together. rotations of loops nicely works for Top, but I have no idea of what this means for a general category (I should have said somewhere that this was my main obstcle in understanding Toen and Vezzosi). , on the other hand, seems to work very nicely form the abstract categorical piont of view, and in the de Rham translation, too. but it does not look like rotations of in Top, at first sight.
but, on second sight... what about the topological inclusion ? isn't that a homotopy equivalence? then everithing works: the right picture is yours, and rotations of loops in Top come from an accidental homotopy with the real thing.
what do you think? -
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
well, I only see this clearly in Top. but there it is quite clear that
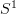 acts on itself by rotations, and that this action on
acts on itself by rotations, and that this action on 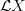 becomes a rotation of the loop,
becomes a rotation of the loop,Yes, and if you look at the diagrams, this is what the transformations between functors
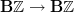 do.
do.I promised I'll insert a diagram, I'll do it now...
-
- CommentRowNumber38.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
sure they have to do this. and this perfectly fits with the toplogical description, where as I was trying to say, every orientation preserving diffeomorphism of is homotopy equivalent to a rigid rotation.
by the way, we'll have to change all -actions in the entry with -actions. -
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
Yes.
So here is what I just typed into the entry, mainly just so we are looking at the same diagrams (which I can't produce here)
I am not sure yet to which extent this sould stay in a more developed version of this entry -- but for the moment it's there, so that we can work on something.
I am a bit short of time. Therefore I have a remark there called "Exercise" which should really be thought of as "if I had had the time, I would have spelled this out".
Have to run now...
-
- CommentRowNumber40.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
fine. I've to go now, too.
here's my plan for tomorrow
i) clean up the subsection on categorical circle action (maybe in the end we could make a separte entry of this, just to be linked from free loop space object, but we'll think on this later)
ii) prove is equivariant with respect to the categorical circle action (this should be almost immediate) -
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
I have now fixed some typos -- in case you were wondering :-)
So in words maybe it's good to say it this way:
if we use the skeleton
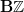 as a model for what could also be modeled as
as a model for what could also be modeled as 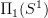 then:
then:the objects of
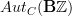 -- labeled by some
-- labeled by some 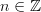 -- describe maps from the circle onto itself that fix the basepoint and have winding number
-- describe maps from the circle onto itself that fix the basepoint and have winding number 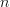
the morphisms in
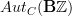 -- labeled by some
-- labeled by some 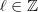 -- describe a rigid rotation of the loop
-- describe a rigid rotation of the loop 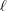 -times around the circle.
-times around the circle.
It is due to
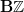 being a skeleton, that only these integer-labeled maps appear, of course. But maybe it's actually useful to make this model explicit.
being a skeleton, that only these integer-labeled maps appear, of course. But maybe it's actually useful to make this model explicit.We should in parallel make the situation for the equivalent model
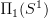 explicit. That will produce a situation that looks much more like the naive circle action that one expects. But together probably both models illustrate nicely how we have to distinguish here between automorphisms of the circle (maps with winding number) and genuine rotations of the circle.
explicit. That will produce a situation that looks much more like the naive circle action that one expects. But together probably both models illustrate nicely how we have to distinguish here between automorphisms of the circle (maps with winding number) and genuine rotations of the circle. -
- CommentRowNumber42.
- CommentAuthorzskoda
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
There is a neat model of Drinfel'd of cyclic objects where a usual circle comes via a categorical limit construction from finite approximations by discrete sets of n points around the circle; a paper few years ago on the arXiv. In your very interesting reasoning above I suspect you are talking also about inertia groupoid of the original groupoid as a model for loop groupoid of original groupoid. I did not hear word inertia groupoid (twisted sectors in the Harvey, Vafa etc. physics parlance) though (but is a good advertising for connections to physics).
-
- CommentRowNumber43.
- CommentAuthorDavidRoberts
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
Hang on, multiplication by n can't be an automorphism of Z, as it isn't surjective! Only multiplication by +/-1 is an automorphism. In other words, Z isn't a divisible group. -
- CommentRowNumber44.
- CommentAuthorDavidRoberts
- CommentTimeFeb 2nd 2010
Also I added a bit about AUT(Pi_1(S^1)) after the 'exercise:...' statement. -
- CommentRowNumber45.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
prove
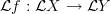 is equivariant with respect to the categorical circle action (this should be almost immediate)
is equivariant with respect to the categorical circle action (this should be almost immediate)I almost missed this, sorry: yes, this statement will be almost tautology, no matter what precisely the categorical circle action actually is concretely.
Because the map
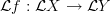 is just post-composition with
is just post-composition with 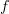 :
: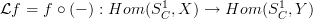
If you wish, in the end it is the exchange law that says that it doesn't matter whether you first have a transformation and then postcompose or first postcompose and then have the transformation.
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
Also I added a bit about AUT(Pi_1(S^1)) after the 'exercise:...' statement.
David, thanks, of course I am being stupid and for
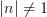 we just have a group homomorphism, not an automorphism.
we just have a group homomorphism, not an automorphism.It's not a drama, we could also be talking about endomorphisms. But I think I'll just fix this the way you indicate...
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
okay, fixed.
So I removed your first query box, David. If you disagree, please put it back in.
Also a quick reply in your second query box.
-
- CommentRowNumber48.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 2nd 2010
I would rather consider only automorphisms of which are isomophic to the identity. this seems to me to better fit the topological picture where rigid rotations are a homotopy equivalent model for the connected component of the identity in the group of homeomorphisms of .
with this restriction (which we could denote to use a notation inspired by the one which is customary in differential topology, where one usually writes ), the only object of is the identity functor and one has . moreover, having only , the categorical circle action on is , which also fits with having be -invariant.
waiting for feedback here before editing the page according to the above. -
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
Domenico,
yes, I agree, that's a way to put it.
But maybe we can start out saying that a priori all of
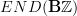 acts on
acts on  , while the "circle action" proper is only the part
, while the "circle action" proper is only the part 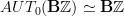 . Because the other parts of
. Because the other parts of 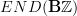 will have a role to play, too. As we said, the
will have a role to play, too. As we said, the  -grading on
-grading on 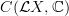 is induced from the action of what on the homology
is induced from the action of what on the homology 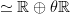 of the circle acts by
of the circle acts by 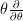 , while the differential is that induced by
, while the differential is that induced by 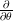 . The first, even, Lie algebra element should correspond to nontrivial objects in
. The first, even, Lie algebra element should correspond to nontrivial objects in 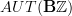 .
. -
- CommentRowNumber50.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 2nd 2010
fine. I'll now edit the entry with the -action, and with as the subgroup giving the circle action. -
- CommentRowNumber51.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 2nd 2010
done. when you have time please have a look. -
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
I am busy reading
David Ben-Zvi, David Nadler: Loop Spaces and Connections.
Lots of answers in there...
-
- CommentRowNumber53.
- CommentAuthorzskoda
- CommentTimeFeb 24th 2010
I read it on Monday evening till 3:30 am and I am tired now.
-
- CommentRowNumber54.
- CommentAuthorzskoda
- CommentTimeFeb 24th 2010
But I also suggest reading together with it those crystals and D-modules notes to which I posted links to in nlab few days ago (e.g. to D-module) and left a note in nforum. The point is that there is not only linear version (D-modules and crystals of qcoh modules), but also nonlinear (D-schemes and crystals of schemes).
http://www.math.harvard.edu/~gaitsgde/grad_2009/SeminarNotes/Nov17-19%28Crystals%29.pdf
-
- CommentRowNumber55.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
at free loop space object I formalized the discussion of how in an -topos the free space object is given by the internal hom object .
This is now in the section Free loop space object – In an -topos.
(The discussion of the induced -action currently given there should be improved by discussing that has a canonical cogroup object structure.)
-
- CommentRowNumber56.
- CommentAuthorDavidRoberts
- CommentTimeNov 24th 2010
Where does the ’’ come from to give you ? Is it the the obvious quotient of an interval with distinct endpoints?
-
- CommentRowNumber57.
- CommentAuthorUrs
- CommentTimeNov 24th 2010
- (edited Nov 24th 2010)
Where does the ’’ come from to give you ?
This is discussed in detail in the entry, starting here.
Under the is just the ! So in you may want to think of it as the fundamental -groupoid of the topological circle.
But what makes all derived loop space and Hochschild cohomology yoga tick is the fact that
as an -pushout. One way to see this formally is to model the -pushout as a homotopy pushout and model that by an ordinary pushout of a resolved diagram in . That resolved diagram can be taken to be
and so this way appears the model for that you have in mind.
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeMay 9th 2012
before I forget: I had added a brief remark on the formulation of free loop spaces in Homotopy type theory
-
- CommentRowNumber59.
- CommentAuthorMike Shulman
- CommentTimeSep 18th 2017
I added to free loop space object an intuitive discussion of how becomes a group object in and acts on all other objects of . Can anyone give a reference where this is worked out precisely and coherently?
When I have some time, I would like to reorganize free loop space object a bit: I think the description of at “as a mapping space object” deserves to be up in the Definition section. In particular it’s not specific to -toposes, but makes sense as a power in any -category. It also yields another definition in terms of ordinary conical limits, namely as the equalizer of the identity map of with itself.
-
- CommentRowNumber60.
- CommentAuthorUrs
- CommentTimeSep 18th 2017
Thanks. Yes, this entry could do with some polishing and re-organization.
-
- CommentRowNumber61.
- CommentAuthorMike Shulman
- CommentTimeSep 20th 2017
Ok, I added some discussion of this perspective to the “Definition” section, but I didn’t try to rewrite the “as a mapping space object” section, so there is a bit of dissonance.
-
- CommentRowNumber62.
- CommentAuthorDavid_Corfield
- CommentTimeSep 20th 2017
Is that just me, or might the reader of
…inducing equivalences for all …
be given a little help with the left term? At first I was looking about for an object of to form the power of.
-
- CommentRowNumber63.
- CommentAuthorMike Shulman
- CommentTimeSep 20th 2017
Sure, I added a parenthetical.
-
- CommentRowNumber64.
- CommentAuthorMike Shulman
- CommentTimeSep 26th 2017
I added a link to this answer for how to construct the action coherently.
1 to 64 of 64