nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorMike Shulman
- CommentTimeJan 25th 2010
Several naive questions at structured (infinity,1)-topos.
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
For idempotence in infinity setting see HTT 4.4.5 with surprising subtleties in the definition (most apparent: it is not a property but involves a choice of structure!), I read that section a month ago and was really delighted with Lurie's reasoning there, which I mostly forgot by now.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 26th 2010
Thanks, I'd really enjoy discussing this.
But this will have to wait a bit. Maybe tomorrow night...
-
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
I would suggest that you change Sh(X) to Shv(X) or Sheaves(X), which is more in line with Lurie's notation and also doesn't step on our ordinary terminology, where Sh(C) is reserved for sheaves of sets. The problem is that the notation Sh(C) is very ambiguous especally when describing sieves or descent, which at least in the case of ordinary stacks, are still stated in terms of sets (that is, the covering sieves are still subfunctors of representable presheaves of sets).
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeJan 26th 2010
Sh(X) can mean in literature a host of other things (for example shape of X) regarding so many words with Sh beginning. I use in my own writings Fas(X) for faisceaux and Ouv(X) for the category of open sets, because Top is the category of top. spaces. But for simplicial sheaves one can use sSh or sFas if s is the prefix for simplicial. I do not feel compelled at all to follow Lurie's notation, though I like most of his choice of terminology. To note he says traditional terms "category cofibered in groupoids" (for what nlab says to my taste uglier opfibration) and "Postnikov tower" (where nlab says to my taste uglier Postnikov systems).
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
That's fair, but denoting it by Sh(X) is confusing when you're talking about descent, which is quite important in the theory of "structured spaces", because, as I noted above, in the ordinary-category version of descent, we have an incomplete categorification, where the sieves are still set-valued subfunctors of representables, which are also taken to be set-valued, but this defines descent for stacks as well. Presumably, this is not the case for (infinity,1)-descent. I don't really care how we denote the (infinity,1)-sheaves, but we should not denote them by Sh(-).
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
an incomplete categorification, where the sieves are still set-valued subfunctors of representables, which are also taken to be set-valued, but this defines descent for stacks as well
It is noteworthy that all present approaches to define higher categorical sites, such as model sites and SSet-sites and Luries (oo,1)-sites, the covers are the the ordinary 1-categorical notion. An (oo,1)-site as currently used is an (oo,1)-category with the structure of a site on its homotopy 1-category!
That need not mean that a more refined notion of oo-site would not exist and be useful, though. In fact, in the 1-categorical case the site structure specifies the sheaf topos structure completely, while in the oo-case there are many (infinitely many, I think) different (oo,1)-toposes with the same underlying (oo,1)-site.
The point is here, and that's I think what your comment is getting at, that for higher category valued sheaves it makes a difference whether we test their descent just on the plain Cech nerves of the covering families, or n-fold hypercovers of these, where we allow new covers of the space of intersections on the previous covers.
A bit on this we have labified at hypercompletion.
But as far as your terminology issue goes: since, as we noted there are many different things one can and does denoted by
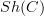 or any of its variants, there is little chance to find a universal choice. The best is to say at top of each text which convention is used. Or, for emphasis, as I do here and there, one can write things like
or any of its variants, there is little chance to find a universal choice. The best is to say at top of each text which convention is used. Or, for emphasis, as I do here and there, one can write things like 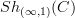 or similar decorated notation to indicate what kind of sheaves one means.
or similar decorated notation to indicate what kind of sheaves one means. -
- CommentRowNumber8.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
Are all of the (infinity,1)-toposes equivalent in any way? Also, has no work been done on defining an (infinity,1) sieve? Descent by looking at the 0th cech cohomology sets in a classical grothendieck pretopology is probably the worst, least canonical way that requires the most choices. In contrast with that, for sieves, the definition is slightly harder, but it's easier if you understand the yoneda lemma. Is there any reason why a naive categorification of a system of covering sieves won't work? I mean, all we need is (infinity,1)-subfunctors of representables and an appropriate yoneda lemma. If you remember, we have that shiny new (infinity,1)-yoneda lemma from mathoverflow. Maybe I'm just being too naive, but the concept of descent by sieves seems to be one that is readily categorifiable without any real work.
Also, the pluralizing topos as toposes is fine, right?
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
Are all of the (infinity,1)-toposes equivalent in any way?
No, they are quite inequivalent. In HTT somewhere in chapter 6 there is a long discussion (over six pages or so) why for instance the Cech-cover descent oo-topos are better behaved than their hypercompletions to hyper-cover descent oo-topos. The latter are what is modeled by the Joyal-Jardine model structure on simplicial presheaves. The former is modeled by the left Bousfield localization of simplicial presheaves just at Cech covers.
These are the two sort of obvious different flavors of oo-stack oo-toposes. But, as discussed in HTT in the section on n-toposes and n-truncated objects, also an n-topos of n-stacks is still an example for an oo-topos on the given site.
So there is a whole infinite (I think) series, at least, of different non-equivalent oo-toposes all associated to one site.
Of course they are not unrelated. Each here is a geometric localizations of the previous one, so you can think of this as a big chain of reflective sub-oo-categories, all sitting in the Cech-local version wich itself of course sits in the oo-presheaves.
has no work been done on defining an (infinity,1) sieve?
I think not. Hm, let me check again in HTT where it's about sieves. Maybe I am misrepresenting it. Search the document for "sieve". But I think, for instance in Structured Spaces, topologies are alsways defined on the homotopy 1-category.
But I entirely agree with you, this should probably be regarded as a gap in the development of the theory. Eventually it would be god to have a notion of oo-topology such that the following statement becomes true:
for C an (oo,1)-category, reflective (oo,1)-subcategories of
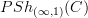 are equivalent to oo-topologies on C.
are equivalent to oo-topologies on C.As far a I can see, nothing like such a theorem has so far been considered. Instead, the definition of sheaf toposes as reflective subcategories is taken as the fundamental definition, and sieves play a secondary role.
-
- CommentRowNumber10.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
What if doing it this way gets us a wrong notion of an (infinity,1)-topos? A good exercise might be to generalize the definition of a sieve to a (2,1) bicategory, and consider sheaves of (2,1)-bicategories. If this gives us a useful notion, then we could use that as a heuristic to test against other constructions, like defining the topology on the truncation.
I guess the idea here is to stop doing topology once we've developed our theory of (infinity,1)-cats. We went to all of this trouble building up an algebraic formalism. Why not use it?
Edit: Are (2,1) bicategories a notion that goes under a different name in ordinary category theory?
-
- CommentRowNumber11.
- CommentAuthorzskoda
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
Urs, I am not sure that the business of n-categorical sieves (as for n=2 paper of Street on 2-dimensional sheaf theory) is equivalent in any sense to the business of n-hypercovers. Toen on the other hand claims that the higher sites in the sense of higher sieves are not appropriate from their experience (which means particular goals!!), but the current version with topology just on the underlying homotopy category is, the statement which I do not like but have no power to challenge. There is in any case more than one kind of higher topoi and higher sites, and I do not think there are wrong and rioght ones but they are likely to serve different purposes.
-
- CommentRowNumber12.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
At least the form of descent I noted is really easy to probe, especially with the yoneda lemma. I see what you mean about there not being a wrong or right way to deal with this though, since both theories reduce the the "correct theory" for n=0,1.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
I don't mean that an n-categorical sieve (whatever that is) is the same as an n-hypercover.
I just said that if you have just ordinary sieves/covering families, then one can see that different notions of higher stacks on these can be obtained by demanding descent with respect to k-fold hypercovers with respect to these covering sieves for different k.
A very detailed discussion of this is in the article by Tibor Beke that is cited at Cech cohomology.
What if doing it this way gets us a wrong notion of an (infinity,1)-topos?
I think one has to change perspective: that ordinary sheaf toposes were defined by the ordinary descent property on Grothendieck covering families was in a way a historical accident. Later it was proven that any sheaf category defined this way is characterized as being a reflective subcategory of the presheaf category, in that there is an equivalence between reflective subcategories and Grothendieck topologies.
Clearly, the notion of a reflective subcategory is the more fundamental one, so this is a good one to use in the definition of more general sheaves, higher stacks. It then becomes converesely a question relevant for practical computations if and how we may characteriz reflective subcategories by descent properties.
And even that is actuall clear: as discussed in HTT, every reflective subcategory is characterized by the collection of local objects, which are defined precisely by the condition that homming local morphisms into them (those that reflect to equivalences) yields an equivalence. This is the descent condition derived from the characterization of reflective subcategory. It is now a matter of taste more than of principle to whicch degree you want to further unravel what this condition means in cocrete data, where it will be some type of descent condition at some kind of covers. This is important to know for computation in applicatins, but I think the abstract definition in terms of reflective subcategories is the more robust way of thinking of the concept of a higher sheaf.
-
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
My understanding is that Beke had an underlying space which is 1-categorical. HTT also looks at (infty,1)-categories, for true higher categories, like bicategories and (infinity,n)-categories, I doubt that these notion would agree with the generalization of the formalism in Street's article. Even for n=2, the Street's formalism in Two dimensional sheaf theory paper is not subsumed in my understanding. Is it ?
Harry said
A good exercise might be to generalize the definition of a sieve to a (2,1) bicategory, and consider sheaves of (2,1)-bicategories.
Look at the Street's article for genuine bicategories. There are some errors however pointed out later by Street, Makkai and Beke in my memory.
-
- CommentRowNumber15.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
@Zoran, By (2,1)-bicategories, I meant categories where the 2-morphisms are all equivalences. Did I mix it up? I guess they should be (2,1)-categories maybe?
@Urs, I was thinking of a descent condition like the really elegant one for sheaves and stacks in terms of sieves, where we want the map Hom(h_X,F) -> Hom(S,F) induced by the inclusion S -> h_X to be an equivalence for any covering sieve S on X for all objects X. That's the definition that seems like it's so perfect for generalization, because the only notions we're working with are equivalences, which are "dimension-independent", representables, which are also "dimension independent", and subfunctors of representables, which also seem like they'd be independent of dimension. Maybe that definition seems so good because it's so slick, but it makes a number of the theorems about descent almost trivial.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeJan 26th 2010
@harry,
yes, and that's the definition that applies generally, for describing reflective subcategories:
they are all described by a collection
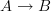 of morphisms as the full sub categories of those objects
of morphisms as the full sub categories of those objects 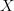 that are local objects with respect to these morphisms, in that
that are local objects with respect to these morphisms, in that![[B,X] \to [A,X] [B,X] \to [A,X]](/extensions/vLaTeX/cache/latex_b69c59569e281c2852870ce163415322.png)
gives a weak equivalence. The Cech models are obtaind by taking
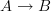 the maps
the maps 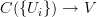 from the Cech nerve of any covering sieve
from the Cech nerve of any covering sieve 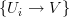 .
. -
- CommentRowNumber17.
- CommentAuthorHarry Gindi
- CommentTimeJan 26th 2010
- (edited Jan 26th 2010)
Oh, then if that's the case, it seems like it's a straighforward generalization of the ordinary sieve approach. Why would you want to take hypercovers, at least in the case of (infinity,1)-toposes? That seems like it would only be important for (infinity,n)-categories for n>1.
-
- CommentRowNumber18.
- CommentAuthorzskoda
- CommentTimeJan 26th 2010
I meant (2,2) categories as genuine bicategories.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
@harry
So the point is: which collection of morphisms
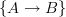 do we want to localize at?
do we want to localize at?Let
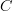 be an ordinary site, for definiteness. For
be an ordinary site, for definiteness. For 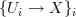 a covering family in
a covering family in  we have
we havethe Cech nerve
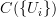 which is a simplicial object in presheaves on the site, and as such an (oo,1)-presheaf. There is the canonical morphisms of simplicial presheaves
which is a simplicial object in presheaves on the site, and as such an (oo,1)-presheaf. There is the canonical morphisms of simplicial presheaves 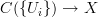
now if we localize (oo,1)-presheaves at all morphisms of this form, then we get the Cech-oo-stacks: a Cech oo-stack
 is a local object for all these morphisms, which means that all the morphisms
is a local object for all these morphisms, which means that all the morphisms![A(X) = [X,A] \to [C(\{U_i\}), A] A(X) = [X,A] \to [C(\{U_i\}), A]](/extensions/vLaTeX/cache/latex_ddf65acc2c26f6a77df3379325be4dcb.png)
are weak equivalences. This is the oo-sheaf condition at Cech covers.
but we could take more morphisms at which we localize. On top of the above sets of Cech cover map, we could take every simplicial presheaf
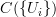 , which is a collection of
coproducts of representables in each degree, and start replacing these representables themselves with Cech covers. Then we take this all together and get a new simplicial object, which is a much more "refined" resolution of the original X, let me call it
, which is a collection of
coproducts of representables in each degree, and start replacing these representables themselves with Cech covers. Then we take this all together and get a new simplicial object, which is a much more "refined" resolution of the original X, let me call it 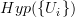 , but there is not one such, but infinitely many (in fact, I think the problem is that hypercovers won't form a small set, even, but a large class).
, but there is not one such, but infinitely many (in fact, I think the problem is that hypercovers won't form a small set, even, but a large class).So now you can in addition demand that an oo-stack should, to qualify as an oo-stack, satisfy descent with respect to all such hypercovers, in that all morphisms
![A(X) = [X,A] \to [Hyp(\{U_i\}), A] A(X) = [X,A] \to [Hyp(\{U_i\}), A]](/extensions/vLaTeX/cache/latex_c236961668fe5c42b20efbdd9060b32c.png)
are weak equivalences. The objects for which this is true are the "hypercomplete" oo-stacks. There are fewer of them, since this is a stronger condition.
But the type of condition is always the same, and always the one you seem to like: we say an object is a local object if homming the morphisms that we want to force to become equivalences into it produces a weak equivalence.
-
- CommentRowNumber20.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
So the main idea that isn't generalizing is the notion of a sieve. What goes wrong if we let covering sieves be subfunctors of the images of the objects under the yoneda embedding satisfying stability under base-change, local character, and identity axoims for a grothendieck topology (obviously not choosing all that satisfy the axioms, but just choosing from among those to generate a topology)? Will that generate an equivalent theory to either one of those two, something in between, or something altogether urelated? Does the notion of a subfunctor even make sense here?
-
- CommentRowNumber21.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
One problem is knowing what a sub-? is. We all know what a subobject is in a category, but what about in the higher categorical setting? For instance, with (symmetric) 2-groups, there are two notions that generalise the kernel of a map of groups, both of which are important. I think what Urs is emphasising is the correct idea, namely, which (families of) maps are just local in character (like an open cover of a space). -
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
I mean, doesn't the yoneda lemma (generalized) give us a canonical embedding of C into [C^op,Kan], and can't we just let subfunctors be subfunctors?
@David: You mean that we're not including base change either? Only local character?
-
- CommentRowNumber23.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
When one considers a general coverage, covers don't necessary pull back to covers - what one gets is a square, but not a cartesian square. Though in practice the pullbacks often exist, and covers are stable, it isn't quite necessary.
-
- CommentRowNumber24.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
A general coverage seems like the wrong notion. Base change is a huge part of the power of a grothendieck topology.
-
- CommentRowNumber25.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
Well, perhaps the idea of using coverages is a little off. But I know that the concept of a sub-thingy is fiddly when working with homotopical objects (or maybe I don't know/get what is state of the art).
a canonical embedding of C into [C^op,Kan], and can’t we just let subfunctors be subfunctors?
but I posit this is a 1-categorical perspective - imagine replacing Kan with the category of homotopy types (however one does this). What is a sub-object? Or what is a sub-n-groupoid, considered as objects of the (oo,1)-category of such things?
I'm just playing devil's advocate a little, because I'd also like to understand what it means to take a subfunctor of
[-,x]:C^op ---> nGpd (or oo-Gpd)
where the codomain is considered as an (oo,1)-category. (Edit, based on Harry's reply: [-,x] is the full Hom, not quotiented by homotopy)
-
- CommentRowNumber26.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
Lurie defines what it means for an infinity-category to be a subcategory of an infinity-category. Also, I would write Hom( - , x), because at least in Switzer, [ - , x] is continuous maps modulo homotopy. We actually want to look at morphisms of simplicial sets not modulo homotopy.
-
- CommentRowNumber27.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
Actually I would write Hom as well, I was being lazy. So if we take an oo-category (is that actualy oo-category, or (oo,1)-category), S(X), the simplicial set of singular simplices of a space, what does this correspond to? Is it invariant under (weak) homotopy equivalences X--> Y of spaces? -
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
Is there any sort of "coherent" (quotes for non-math sense) notion of a sub kan-complex? I mean, don't we have a subobject classifier for SSet? Or is that notion of "being a" kan subcomplex too strong?
-
- CommentRowNumber29.
- CommentAuthorMike Shulman
- CommentTimeJan 27th 2010
I looked away from my computer for a day and got completely lost by this discussion, but I know that in the world of 2-topoi, I think the right notion of "subobject" (or "1-subobject" if you prefer to be more precise) is a fully faithful map. The corresponding thing in (oo,1)-topoi would be a map that is (representably) an inclusion of a subset of connected components. (The subobject classifier in sSet is basically irrelevant, having no homotopical meaning.) But I'm guessing the notion of "sieve" arising from this will be only the existing notion of topology on an (oo,1)-category, still not able to distinguish hypercompleteness.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
by the way Mike, in case you missed it, I started replying to your original question in this thread here in another thread...
-
- CommentRowNumber31.
- CommentAuthorTobyBartels
- CommentTimeJan 27th 2010
We all know what a subobject is in a category
Although there is a standard default meaning of ‘subobject’, actually even for an ordinary 1-category it is the wrong notion, as in Top (meaning the category of spaces up to homomorphism). See the discussion in Section 7 (on page 117 or 122, in either case between 7.76 and 7.77) in The Joy of Cats.
I don't think that this is terribly relevant; we all know what a subobject is in a topos, so hopefully it's no less clear what a subobject (or 1-subobject, following Mike) is in an (oo,1)-topos. My point is that reducing a notion to ‘subobject’ should not make anyone feel that it has been fully clarified.
-
- CommentRowNumber32.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
I agree, Toby. Given the n+1-stage factorisation system of a map of n-types, we have different notions of injectivity. I should have pointed this out first up, to make my point more simply.
-
- CommentRowNumber33.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
well, knowing what a sub-infinity-category is up to equivalence seems like it's good enough, am I mistaken?
-
- CommentRowNumber34.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
That's true, but there are 1-sub-oo-categories, 2-sub-oo-categories and so on. There is an m-poset of k-sub-oo-categories for some appropriate values of m and k that I can't think of right now. I suppose the choice has to be application driven, and Mike's suggestion is as good as any unless it is necessary to change (in my own work, I take a map 'including' a sub-2-group to be a faithful functor (or locally faithful, if dealing with the deloopings) - this would be a 2-subobject perhaps)
-
- CommentRowNumber35.
- CommentAuthorHarry Gindi
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
Well, yeah, but we're looking at (infinity,1)-categories, which means that we can't just keep constructing examples like that. Our notion of equivalence requires us to have an SSet map in that induces an isomorphism in the homotopy category, so I think our notion of equivalence is more robust than that. Also, the notion of a sieve being a subfunctor really only needs to be "up to equivalence" because we require our covering sieve system to be stable under (homotopy?)-pullbacks anyway.
-
- CommentRowNumber36.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
You've convinced me :) And you're right about the 'up to equivalence' bit - we certainly would want homotopy pullbacks.
-
- CommentRowNumber37.
- CommentAuthorMike Shulman
- CommentTimeJan 28th 2010
The reason I say that 1-subobjects = fully faithful maps are the "right" notion of subobject for 2-topoi is that using them you get the 2-Giraud theorem. Cf. Street "characterization of bicategories of stacks". I certainly agree that 2-subobjects = faithful maps are useful for other purposes.
-
- CommentRowNumber38.
- CommentAuthorHarry Gindi
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Oh, quick question. Does the duality between fibered categories and pseudopresheaves generalize to right fibrations of simplicial sets and simplicial presheaves? I use the term "duality" loosely here.
@Mike: If we restrict our sieves to be fully faithful (in the appropriate infinity,1-category sense), can we recover either of the covering methods Urs was talking about?
-
- CommentRowNumber39.
- CommentAuthorMike Shulman
- CommentTimeJan 28th 2010
I think that with oo-sieve = 1-subobject of a representable in the sense I advocated, you will end up with Cech descent.
-
- CommentRowNumber40.
- CommentAuthorHarry Gindi
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
@Mike: Well, whatever characterization of 2-toposes has brought you to that (admittedly informal) conclusion seems like it is a promising one. I hope I've appropriately disclaimed you from the next paragraph.
Deferring to Mike, who has not written up a formal proof of this statement (I only qualify this because I don't want to claim something that might oblige him to actually write up a proof [or force him to repudiate earlier statements that he did not make]), this agrees with Lurie's conclusion that the Cech covering definition is the correct one, at least for (infinity,1)-categories. Perhaps for (infinity,n)-categories, we need the hypercover definition more, but from what I've seen, the case of (infinty,1)-categories is a canonical extension of 1-categorical intuition. It may turn out that for (infinity,n)-categories, we will need the more precise information given by hypercovers.
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Lurie's conclusion that the Cech covering definition is the correct one,
I wouldn't quite put it that way. A priori every localization is as "right" as any other. What he does, though, it spend six pages on pointing out that the Cech localizations are particularly well behaved with respect to several other constructions. So maybe these are the "most natural" ones.
-
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Notice that one main point that one might feel is wrong about Cech localizations is that the Whitehead theorem generally fails in them. It is precisely their further hypercompletion to hypercover localizations that makes the Whitehead theorem come out. If in your applicaiton Whitehead's theorem is crucial, then hypercover descent will induce the "right" notion of localization for you.
-
- CommentRowNumber43.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
Hypercovers come a lot and essentially in Hodge theory for algebraic varieties (as in 1970s papers of Deligne), though I am not competent to defend the particulars of this.
-
- CommentRowNumber44.
- CommentAuthorMike Shulman
- CommentTimeJan 28th 2010
My contention that sieves as 1-subobjects gives you Cech descent is supported by appendix A of Hypercovers and simplicial presheaves, although they only consider 1-sites rather than (oo,1)-sites.
-
- CommentRowNumber45.
- CommentAuthorHarry Gindi
- CommentTimeJan 28th 2010
Is there an analogous condition for 1-sites to have descent by hypercovers?
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
You mean for 0-stacks = sheaves? There one can't see the difference: homming a Cech nerve into a set-valued presheaf yields the same result as homming any of its hypercover refinements into it.
-
- CommentRowNumber47.
- CommentAuthorHarry Gindi
- CommentTimeJan 28th 2010
I meant for 1-stacks, which is really the only place we might be able to get a glimpse of it. Either that or in one of Street's papers on 2-stacks (if such papers even exist. I assume they do, but I may have misunderstood the other people in this thread).
-
- CommentRowNumber48.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
Yes, for 1-stacks it already matters. 1-stacks see "1-step" hypercovers. In general, n-stacks will see "n-step hypercovers". The good reference for this is the article by Tibor Beke that is referenced at Cech cohomology.
-
- CommentRowNumber49.
- CommentAuthorHarry Gindi
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Ah, then the case is closed, at least from my perspective. Ordinary descent by sieves appears to generalize directly, and "hyper-descent " is a generalization of a lower-dimensional process as well. It's really nice when things generalize smoothly like that, because it gives some sort of direct confirmation that it's a canonical extension of the earlier theory.
One of the main reasons I was interested in the classical formulation of descent generalizing fully is that this is the form one would expect to generalize to "abstract (oo,1)-categories", which are something like our idealized notion of what an (oo,1)-category should look like. This formulation of descent doesn't depend on any of the underlying machinery of quasicategories, so it feels more "right". Formulating these kinds of things as abstract properties that use terms that are completely relative to the background seems like a very useful technique. Notions like equivalence, subobject, representable, etc., all have a well-defined meaning relative to your chosen model of (infinity,1) category. The distinction is something like the distinction between material and structural set theories, at least in my mind.
Or I could be completely wrong. ;) I'm sure someone will correct any egregious errors I've made in my assessment.
-
- CommentRowNumber50.
- CommentAuthorMike Shulman
- CommentTimeJan 29th 2010
Can you say exactly where in Beke's paper he talks about 1-stacks? Briefly glancing at it I don't see the connection. I am also confused because the DHI paper "Hypercovers and simplicial presheaves" claims that Cech descent implies descent for all "bounded hypercovers." Is that not contradictory to saying that for 1-stacks the hyperness already matters?
A stray thought: could 1-step hypercovers be identified with "sieves that are 2-subobjects" in the same way that 0-step, i.e. Cech, hypercovers are identified with "sieves that are 1-subobjects"?
-
- CommentRowNumber51.
- CommentAuthorDavidRoberts
- CommentTimeJan 29th 2010
Cech covers are cofinal in bounded hypercovers, because the refinement process is guaranteed to stop after a finite number of steps, but not all hypercovers.
-
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
Right, thanks, I should have mentioned that, for completeness.
But I was just making the much more trivial comment in reply to something Harry said, that an n-groupoid valued presheaf will only care about n-step hypercovers being hommed into it, it can't tell if its an n+1-step hypercover, actually. That's why when talking about just sheaves, the question of hypercovers never arises.
But, yes, if you already know that the n-groupoid valued presheaf produces an equivalence after homming a projection out of any Cech-nerve into it, then the same will be true for homming all bounded hypercovers into it, as you point out.
What Beke's article shows is that if you start with an n-groupoid valued presheaf, then in order to n-stackify it (hence oo-stackify it) i.e. in order to refine it to something that does satisfy descent with respect to all Cech covbers, it is sufficient to do what for sheaves is called the "+-construction" at n-step hypercovers.
I should have been clearer about this. In fact, we should have all this cleanly said on some nLab page eventually. I suppose currently aspects of this must be hidden somewhere at descent and Cech cohomology.
-
- CommentRowNumber53.
- CommentAuthorDavidRoberts
- CommentTimeJan 30th 2010
Ah, of course - as an n-groupoid is (n+1)-coskeletal (approximately - I may have the indexing out by one) it only sees a skeleton of a hypercover, and so a bounded hypercover. Cool!
-
- CommentRowNumber54.
- CommentAuthorMike Shulman
- CommentTimeJan 30th 2010
Oh, okay, I see. I don't think it's correct, then, to say as Harry did that "hyper-descent is a generalization of a lower-dimensional process"; do you? It's only when you get to the oo-world that you can tell the difference between "satisfying descent" and "satisfying hyperdescent," even if you may want to look at n-step hypercovers when sheafifying n-presheaves.
-
- CommentRowNumber55.
- CommentAuthorHarry Gindi
- CommentTimeJan 31st 2010
- (edited Jan 31st 2010)
Hmm, consider this. We have (n,r)-categories (roughly). For regular descent, our notion our notion of descent should be r-descent, while hyper-descent is going to be the full n-descent, call this overdescent (perhaps?). When we get into (oo,r)-categories, then all notions of overdescent become the same thing, hyperdescent. I'm betting that with this scheme, we'll end up with two cases: toposes that act like higher grothendieck toposes, and toposes where whitehead's theorem holds. However, this is really just unfounded speculation, but it seems like that's how it should be. -
- CommentRowNumber56.
- CommentAuthorDavidRoberts
- CommentTimeJan 31st 2010
I wonder if there is a notion of 'bounded descent' - say one is looking at cohomology with coefficients with values in n-groupoids, for arbitrary n all at once -or more concretely, with values in bounded complexes. Then one needs bounded hypercovers of arbitrary degree, but not full hypercovers. But maybe I'm being stupid, and this is really cohomology with coeffs coming from the (oo,1)-cat of bounded groupoids (=colimit of {nGpd} over all n) -
- CommentRowNumber57.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
Mike wrote:
I don't think it's correct, then, to say as Harry did that "hyper-descent is a generalization of a lower-dimensional process"; do you? It's only when you get to the oo-world that you can tell the difference between "satisfying descent" and "satisfying hyperdescent," even if you may want to look at n-step hypercovers when sheafifying n-presheaves.
Yes, I guess one should formulate this carefully enough.
Harry wrote:
I'm betting that with this scheme, we'll end up with two cases: toposes that act like higher grothendieck toposes, and toposes where whitehead's theorem holds.
I think I see what you are maning to get at, but maybe this requires a more detailed analysis. I don't think it is right to think of there just being two different types of descent for oo-stacks on a given Grothendieck topology. There should be many many more, one for every left exact localization of the oo-presheaf oo-category. In HTT for instance there is a whole section on n-toposes (meaning (n,1)-toposes) and all of them are examples of (oo,1)-toposes on the given site.
But I can't claim that I have a good systematic understanding of the different notions of descent. Certainly Cech descent is what one wants to look at in most cases. Notably for instance in Lurie's later developments such as in Structured Spaces, the main ambient oo-toposes are taken to come from Cech descent, as far as I am aware.
1 to 57 of 57