nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
nLab > Latest Changes: Topological Quantum Field Theories from Compact Lie Groups
Bottom of Page1 to 13 of 13
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
created an entry titled Topological Quantum Field Theories from Compact Lie Groups
on the recent (or not so recent anymore) article by Freed-Hopkins-Lurie-Teleman (therefore the capizalization).
I typed into this a summary of their central proposal for how to formalized the path integral quantization for "direcrete" quantum field theories, in terms of higher category theory.
I think this is important, and is actually a simple idea, but few people having looked at the article maybe get away with the take-home message here. So I tried to amplify this.
I also have some own thoughts about this. So I put a big query box in the end, with a question.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
going along with this: some further additions to higher category theory and physics, section stub on the path integral as higher categorical
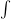 and references on that topic.
and references on that topic. -
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 30th 2010
apparently, there's a little inconsistency on the definitin of objects in : in the abstract categorical definition, an object is a functor , but in the QFT interpretation it becomes a functor . I do not know which to choose, so I'll not edit the page right now. -
- CommentRowNumber4.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 30th 2010
added a comment into the query box -
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 31st 2010
edited a bit the entry, choosing the version, which seemed to me to better fit the general construction. also edited my comment in the query box. -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 31st 2010
I'll write here for a while to avoid editing the query box every five minutes...
Let us think to the basic idea in extended TQFT, before its formalization: we have some nice functor Z:manifolds --> algebraic data and we want to compute it on a given manifold M. what we'd really like to do is to is to dismount M into simplices, compute Z on each simplex and reassemble the data to get Z(M). so an extended TQFT appears to be (ot at least aims to be) a theory of simplices, with Bord roughtly a category of "stuff which can be built by glueing simplices together".
from this point of view, the category of simplices should sit inside Bord, and functors Z: Bord --> C (where C is some infinity-category) should be the extension of their restriction to simplices, which are therefore the fundamental object from this point of view.
one can straightforwardly generalize this to Bord(X), considering functors stemming from simplices in X, i.e. representations of the Poincare' infinity-groupoid of X, as the starting point to build an extended TQFT.
this should be what Urs wonders about in the query box, am I right? -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
apparently, there's a little inconsistency on the definitin of objects in
An object in
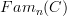 is a functor
is a functor 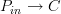 , but a morphism then is a natural transformation between the functors
, but a morphism then is a natural transformation between the functors 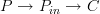 and
and 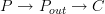 . The components of this natural transformation is itself a functor
. The components of this natural transformation is itself a functor ![P \to [I,C] P \to [I,C]](/extensions/vLaTeX/cache/latex_b97062ac10c85ae7c6951e613f27770e.png) . That's what I meant to express. But should be clarified.
. That's what I meant to express. But should be clarified.this should be what Urs wonders about in the query box, am I right?
This is certainly one aspect, and not the least one, yes. However, the central aspect that I was driving at is this potential reformulation of the discussion where
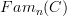 appears explicitly to a discussion where it just appears implcitly as a way to express the extension of a functor out of
appears explicitly to a discussion where it just appears implcitly as a way to express the extension of a functor out of 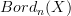 to a functor just out of
to a functor just out of 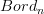 .
.I agree with your query box comment that this is somehow about "representable" QFTs in some sense. Indeed, a sigma-model QFT should be thought of as a QFT that is "represented" by a geometric object in some sense. Precisely in which sense, though, is part of the question, still.
I should also say that I intentionally just wrote "extension" instead of "Kan extension". While in some toy examples Kan extension seems to lead to the right answer, in other toy examples it seems to lead to an unexpected answer. I am currently not really sure what kind of extension it is. Possibly it is a Kan extension all right, but only if one takes due care of doing the right higher categorical Kan extension. Unfortunately I have very little technical control over (oo,1)-categorical Kan extensions, let alone (oo,n)-categorical ones. Even HTT gives only a partial discussion of (oo,1)-Kan extensions. And model category theoretic models seem not much better understood.
This is currently my main technical stumbling block here. Also notice that the article by Freed/Hopkins/Lurie/Teleman is at best vague about what their integration functor
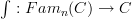 (which by my conjectural idea should somehow compute this extension ) does on morphisms. On objects its the (oo,n)-categorical colimit, but on morphisms it is less clear.
(which by my conjectural idea should somehow compute this extension ) does on morphisms. On objects its the (oo,n)-categorical colimit, but on morphisms it is less clear.Johan Alm looked into this in some detail for the plain 1-categorical context. The trouble is that the obvious abstract-nonsense definition for what happens on morphisms is not functorial. One can "fix" it by hand, though. But not uniquely. One way to fix it yields effectively a generalizations of John Baez's "degroupoidification" map (he implcitly considers the special case where the objects in
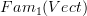 are functors constant on the ground field). It turns out though that there is at least one other way to write down a functorial formula that restricts to taking colimits on objects. With this trouble already present in the 1-categorical case, I am currently left a little puzzled about how the integration functor is properly defined in general higher categorical case.
are functors constant on the ground field). It turns out though that there is at least one other way to write down a functorial formula that restricts to taking colimits on objects. With this trouble already present in the 1-categorical case, I am currently left a little puzzled about how the integration functor is properly defined in general higher categorical case. -
- CommentRowNumber8.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
- (edited Oct 22nd 2012)
This is certainly one aspect, and not the least one, yes. However, the central aspect that I was driving at is this potential reformulation of the discussion where appears explicitly to a discussion where it just appears implicitly as a way to express the extension of a functor out of to a functor just out of .
Sure. What I wanted to stress is that the very neat ’ as a tool’ point of view as you present it in the query box (which, by the way, I like a lot) only applies when you have an object and a functor out of . in this sense as the basic object would seem more general. yet, it should be possible to think to a functor as to a functor , with a sort of generalized object representing the QFT (in some sense to be clarified).
but let us start with something concrete: what are we able to do for n=0? and for n=1?
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
only applies when you have an object

oh, I see, yes, that's true. So this looks more restrictive than the
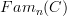 -description, right.
-description, right.It is noteworthy, though, that there don't seem to that many examples of quantum field theories that would no fit this apparently more restrictive picture. Notably all gauge theories are part of this picture, obtained by setting
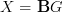 .
.but let us start with something concrete: what are we able to do for n=0? and for n=1?
Good point. I am not sure if you are aware of our last attempt to tackle this: Johan Alm, a grad student from Stockholm, had started looking at these cases. One page documenting some stage of this is at Quantization as a Kan Extension. He had various further computations and proofs later on.
This all looked very promising. But somehow the feeling was that those toy examples were too toyish and stepping beyond proved difficult. I think we ran out of energy at some point and now the project is dormant. I would enjoy seeing it re-activated, though I feel now that one needs to be careful, as the fruit to be picked here needs serious pulling to get off.
-
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 1st 2010
indeed, I was not aware of Quantization as a Kan extension. now that I am, I'll study that and then come back :-) -
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
I've now looked at Johan Alm paper. it's very interesting and neatly written. let me stress a point which I think deserves more attention: the construction seems to nicely work with respect to refinements: if X_2 is a finite subgroupoid of (in the notations of the paper) refining a finite subgroupoid X_1 of , then by the universal propery of left Kan extensions, maps canonically to . and, if there were the looked for functor , then (universal property again), the unique morphism would factor as . that is, the approximation from below is a better approximation from below than . or: a better approximation to gives a better approximation to . but the very same thing happens for approximations from above (right Kan extensions). so I'd think to a left integral which is the limit of the left approximations on the poset of finite subgroupoids of (this limit should exist by monotony) and of a right integral which is the limit of the left approximations. if the two limits are isomorphic (via the natural maps between them provided by the construction) then they would be (nothing but the dear old integration a la Riemann..) -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJun 12th 2012
- (edited Jun 12th 2012)
added in this new subsection with notes taken in a talk by Constantin Teleman, with plenty of new results on this topic.
-
- CommentRowNumber13.
- CommentAuthordomenico_fiorenza
- CommentTimeOct 22nd 2012
One of the main point in the Freed-Hopkins-Lurie-Teleman paper is the construction of the "path integral" morphism (a monoidal functor) . On the other hand, there should be also an obvious morphism (again, a monoidal functor) which looks at as to the category of -local systems over the point. not sure of which the relation between these two should be (vaguely in my mind the former should be thought of as a pushforward and the latter as a pullback, and in some sense they should be adjoint, but all this is still out of focus in my mind).
1 to 13 of 13