nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
can anyone point me to some useful discussion of cosismplicial simplicial abelian groups
![\Delta \to [\Delta^{op}, Ab] \Delta \to [\Delta^{op}, Ab]](/extensions/vLaTeX/cache/latex_d1cc8ee3ed1bc3649a9309085cdbd8e6.png)
and cosimplicial simplicial rings
![\Delta \to [\Delta^{op}, CRing] \Delta \to [\Delta^{op}, CRing]](/extensions/vLaTeX/cache/latex_5d63c4f0c914aa3a558311cfc687015e.png)
I guess there should be a Dold-Kan correspondence relating these to unbounded (co)chain complexes (that may be nontrivial both in positive as well as in negative degree). I suppose it's kind of straightforward how this should work, but I'd still ike to know of any literature that might discuss this. Anything?
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
But the totalization functor in either the second or in the third quadrant still give unboundedness in one direction only, isn't it ?
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
Am I mixed up? Let me see.
We have a double complex
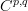 with one differential increasing
with one differential increasing 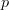

and the other decreasing
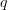
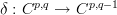
This gives me single differential
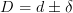
of definite degree (say +1) if the total degree is taken to be
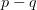 .
.So if both
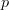 and
and 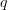 ranged in
ranged in 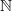 this gives degrees in all of
this gives degrees in all of 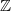 .
.And I'd think this is what I get from forming the chain complex of a cosimplicial simplicial abelian group: a chain complex (
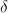 ) of cochain complexes (
) of cochain complexes (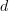 ).
).Do you agree?
1 to 3 of 3