Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: homotopy group of an oo-stack

Bottom of Page

1 to 76 of 76

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    I am expanding the entry homotopy group (of an infinity-stack) by putting in one previously missing aspect:

    there are two different notions of homotopy groups of oo-stacks, or of objects in an (oo,1)-topos, in general

    • the "categorical" homotopy groups

    • the "geometric" homotopy groups.

    See there for details. This can be seen by hand in same cases That this follows from very general nonsense was pointed out to me by Richard Williamson, a PhD student from Oxford (see credits given there). The basic idea for 1-sheaves is Grothendieck's, for oo-stacks on topological spaces it has been clarified by Toen.

    While writing what I have so far (which I will probably rewrite now) I noticed that the whole story here is actually nothing but an incarnation of Tannak-Krein reconstruction! I think.

    It boils down to this statement, I think:

    IF we already know what the fundamental oo-groupoid 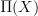\Pi(X) of an object 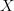X is, then we know that a "locally constant oo-stack" with finite fibers is nothing but a flat oo-bundle, namely a morphism 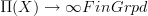\Pi(X) \to \infty FinGrpd (think about it for n=1, where it is a very familiar statement). The collectin of all these is nothing but the representation category (on finite o-groupoids)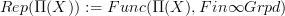

    Rep( \Pi(X)) := Func(\Pi(X), Fin \infty Grpd)

    For each point 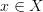x \in X this comes with the evident forgetful funtor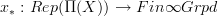

    x_* : Rep(\Pi(X)) \to Fin \infty Grpd

    that picks the object that we are representing on.

    Now, Tannaka-Krein reconstruction suggests that we can reconstruct 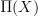\Pi(X) as the automorphisms of the functor.

    And that's precisely what happens. This way we can find 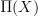\Pi(X) from just knowing "locally constant oo-stacks" on X, i.e. from known flat oo-bundles with finite fibers on X.

    And this is exactly what is well known for the n=1 case, and what Toen shows for oo-stacks on Top.

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010

    reading a bit more, I see that this is how Grothendieck thought of this in the first place. All the better! :-)

    I am busy restructuring a bit more...

    • CommentRowNumber3.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 4th 2010
    What about the dependence on the topology on X? For schemes the Zariski topology isn't enough, one needs the etale topology to get the algebraic fundamental group.

    Also, knowing the finite covering spaces only gets the profinite fundamental group (and I think only in the locally connected case) - compare with work by Marta Bunge and collaborators on fundamental group(oid)s of toposes. More generally there is a prodiscrete fundamental group, but I don't really know anything about this.
    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010

    Thanks, David, I was hoping you would chime in.

    Yes, I am aware of these subtleties. But I don't yet quite know a good elegant way to discuss them.

    Maybe you feel like filling in some of the standard story into the entry? I have meanwhile rewritten the Idea-section a bit.

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    In his TWF 182 John Baez mentions Toen's paper at the end and says about it

    This answers the question: "the fundamental group is to covering spaces as the whole homotopy type is to... what?"

    So the answer is this: if for covering space we say "finite bundle", then:

    The fundamental group is to finite bundles as the whole homotopy type is to finite oo-bundles.

    It's a pretty plausible statement, but that's what Toen actually proves -- if you grant me that a locally constant oo-stack is the oo-stack of sections of a finite oo-bundle.

    • CommentRowNumber6.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 4th 2010
    • (edited Feb 23rd 2010)
    Talking about the difference between manifolds and schemes, the former being a proxy for locally well-behaved spaces, would probably be a good idea.

    Perhaps the example of a covering space spec(K) --> spec(k) for a finite field extension k --> K would be good, as topologically this is not very interesting, but as schemes this is of course the whole point of Galois theory (at least from Artin's POV), and etale covers are essential. I'm afraid I don't have much time today, but will get onto it when I can.

    The relation between a locally constant sheaf and a local system is where the subtlety lies - going from a functor O(X)^op -> Set to a functor Pi_1(X) -> Set is very interesting. (O(X) here denoting the site arising from the Grothendieck topology)
    • CommentRowNumber7.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    Bit of a cross-over there on comments :)

    if you grant me that a locally constant oo-stack is the oo-stack of sections of a finite oo-bundle.

    well this is a theorem to be proved, really. Polesello-Waschkies in 'Higher Monodromy' proved that locally constant stacks are the same as 2-functors $\Pi_2(X) \to Gpd$, but they didn't have a notion of 2-bundle with (weakly) discrete fibres (let alone weakly/2-finite ones). One thing I intend to do one day is to prove the equivalence between 2-covering spaces and locally constant stacks, but, to quote Galois, I have no time.

    I would say the 'profinite fundamental group is to finite bundles...', but then the notion of profiniteness for locally constant stacks is not yet well-defined, and the subject of a somewhat stalled (sorry Tim!) project.

    • CommentRowNumber8.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 4th 2010

    Somewhat stalled indeed! I had a student start on in in 1983 or there abouts, but with the Iran-Iraq war, his fleeing from his home country and ending up in northern Norway, and us loosing contact completely, I followed it up with a later student (this time it was Saddam's invasion of Kuwait and the first Gulf War, that student fleeing with his family to Turkey on foot, and ending up in Australia some time later). If someone wants to cause another war and refugee crisis their input would be very well received!

    My feeling is that the top down' approach works but it needs the bottom up (i.e. profinite 2-group classifies locally constantfinite' stacks' to start with), to connect with Galois and Grothendieck. I still do not understand what 2-Galois theory really looks like and am not 100% convinced by the tales that people tell about it. Bertrand's work went a long way in that direction (and I have not had the chance to hear him talk about it nor talk to him about it recently) but I felt it still was not a clear as Grothendieck's original letters suggested should be possible.

    • CommentRowNumber9.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 4th 2010

    OOps. I got the wrong inverted comma there!

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    Polesello-Waschkies in 'Higher Monodromy' proved that locally constant stacks are the same as 2-functors $\Pi_2(X) \to Gpd$,

    Thanks for this reference!

    Any further references that I should be aware of?

    One thing I intend to do one day is to prove the equivalence between 2-covering spaces and locally constant stacks, but, to quote Galois, I have no time.

    Hm, I may be wrong, but it would seem to me that the nontrivial aspect of the story is what Polesello-Waschkies show for n=2 (and essentially what Toen shows, for n=oo), that locally constant stacks on a topological space are given by functors \Pi_2(X) \to Grpd .

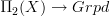    The relation of this to cover-2-spaces should just be a bit of abstract nonsense, I'd think. Well, maybe I am wrong, but I would argue like this:

    unless I am mistaken, the universal cover of a connected topological space X can be thought of as the 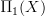\Pi_1(X)-principal groupoid bundle classified by the canonical functor 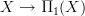X \to \Pi_1(X) that is the constant path inclusion, i,e. thought of as the homotopy pullback over 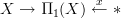X \to \Pi_1(X) \stackrel{x}{\leftarrow} * for some chosen basepoint x.

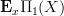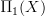    For to compute this homotopy pullback we replace the point equivalently by the groupoid \mathbf{E}_x \Pi_1(X) whose objects are paths starting at x and whose morphisms are commuting triangles of morphisms in \Pi_1(X), the prohection 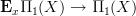\mathbf{E}_x \Pi_1(X) \to \Pi_1(X) picking out the bottom edge of these triangles.

    Then the desired homotopy pullback is the ordinary pullback of 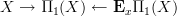X \to \Pi_1(X) \leftarrow \mathbf{E}_x \Pi_1(X). That is the space whose elements are homotopy classes of paths in X, starting at x. QED.

    Moreover then, an arbitrary covering space is an associated bundle for this, associated by a representation 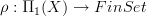\rho : \Pi_1(X) \to FinSet, hence the homotopy fiber of X \to \Pi_1(X) \stackrel{\rho}{\to} FinSet .

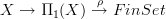    Given this, I would tend to think that the right definiton of universal oo-covering space of a connected space is the principal oo-bundle classified by 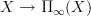X \to \Pi_\infty(X). Similarly an arbitrary covering space I would define to be the homotopy fiber of a morphism of the form X \to \Pi_\infty(X) \to Fin \infty Grpd .

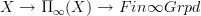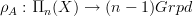    Does that sound like cheating? To me this sounds like the right definition of what covering space should mean. If you grant me this (just for a second) then of course with Toen et al's results which identify locally constant n-stacks A with representations \rho_A : \Pi_n(X) \to (n-1) Grpd (as far as they actually do) we have then also an identification of locally constant n-stacks with covering n-spaces, simply by forming the homotopy fiber of X \to \Pi_n(X) \stackrel{\rho_A}{\to} Fin \infty Grpd.

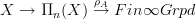    Polesello-Waschkies make the representation 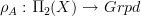\rho_A : \Pi_2(X) \to Grpd explicit for 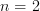n = 2 . To get the same from Toen's result, one would have to do one Tannakian reconstruction step, I suppose.

    • CommentRowNumber11.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 4th 2010
    You are on the money as far as the universal oo-covering space goes (or any of its truncations to finite n) - I realised this around the time of our 'inner automorphisms' paper. The trick is the right context for higher covering spaces. I was deliberately taking a 'low-brow' approach in my thesis, i.e. no simplicial sheaves, partly because I didn't really understand them, and I wanted to make contact with Toby's work. One of Tim's students had an idea of passing from a locally constant stack to a sort of 2-etale space, but I'm not really convinced that all the details were worked out (maybe they were and never made it to the thesis - I can sympathise on that note). Personally I think that even if one take a simplicial sheaf type approach to building geometric objects corresponding to locally constant n-stacks, they should be representable as long as the space is locally well-behaved - but this may be more of a wish-list :)

    Perhaps I have my sights set too low as far as the power of the abstract nonsense goes: I would define higher covering spaces as locally trivial topological n-groupoids over a space (or internal to whatever category the base 'space' lies in), and then recover the homotopy fibre point of view.
    • CommentRowNumber12.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 4th 2010
    In other words, I agree with Tim on the need for a bottom up approach - as well as top-down for the really fancy stuff so as to meet in the middle. I'd be interested to hear from Tim what tales of 2-Galois he has been told (unless one of the ones he doesn't believe is mine! Or perhaps I need telling my ideas are foolish :P)
    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010

    Thanks, David. It is only now that I remembered that we do have an extensive nLab page covering space and that in the very last query box there, you make precisely the point that I mentioned in my above comment.

    I think I'll work on this page now a bit, to amplify this point of view more. I have to digest the construction that Todd spells out there, but I bet this may be understood as another way of computing the homotopy fibers of the constant path inclusion X \to \Pi_1(X)

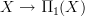
    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    I would define higher covering spaces as locally trivial topological n-groupoids over a space

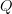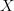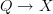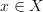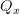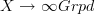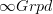    Yes, agreed. But now how would we say this? We want a topological infinity-groupoid Q over X whose fibers are topologically discrete (finite) groupoids. So we need a morphism Q\to X satisfying first of all the property that over each x \in X the fiber Q_x is a discrete groupoid. This says we have a morphism X \to \infty Grpd, where we regard the \infty-groupoid \infty Grpd of discrete oo-groupoids itself as a topological \infty-groupoid in the evident way.

    I was going to say what the evident way is, but let me think about it for a second... ;-)

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    I was going to say what the evident way is, but let me think about it for a second... ;-)

    Here we go:

    regarded as a topological oo-groupoid, the oo-groupoid of all finite oo-groupoids -- which maybe properly I should denote 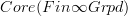Core(Fin \infty Grpd) -- is nothing but the oo-stack on Top that is constant (in the sense of constant sheaves) on 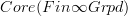Core(Fin \infty Grpd) , hence the oo-stackification of the oo-groupoid valued presheaf that is constant (in the genuine sense) on Core(Fin \infty Grpd) .

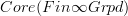    This gives rise to a grand tautology then, which should clarify the notion of oo-covering space: for by definition of oo-stackification now, the topological oo-groupoid incarnation of 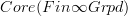Core(Fin \infty Grpd) will send a topological space to something that is glued on a cover of that space from a finite oo-groupoid over each patch. But that's what an oo-covering space is suposed to be. So this constant stack on 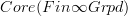Core(Fin \infty Grpd) is in fact the classifying stack for oo-covering spaces and accordingly morphisms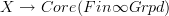

    X \to Core(Fin \infty Grpd)

    classify oo-covering spaces on X. It's just abstract nonsense. But if you think about it, it is also the right answer.

    toy version

    In fact, let's look at the decategorification of this. I claim that the stack on 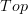Top that is the stackification of the presheaf constant on the groupoid 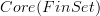Core(FinSet) of finite sets is the classifying object for covering spaces: by definition for X a topological space the value of this stack on X is the groupoid whose objects are represented by tuples consisting of a cover of X, a finite set over each patch, an isomorphism of finite sets over each double overlap, such that this is consistent on triple overlaps. But that's of course a covering space on X.

    If you now say "But that's trivial!" then I'll say "Right, and that's my point: the relation beween oo-covering spaces and locally constant oo-stacks is trivial!" :-)

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010
    • (edited Feb 4th 2010)

    ...

    • CommentRowNumber17.
    • CommentAuthorUrs
    • CommentTimeFeb 4th 2010

    I rewrote the Idea section for geometric homotopy groups of an oo-stack.

    • CommentRowNumber18.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 4th 2010

    So this constant stack on 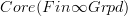Core(Fin \infty Grpd) is in fact the classifying stack for oo-covering spaces and accordingly morphisms

    I'm impressed! This is precisely what Polesello-Waschkies prove for locally constant stacks, namely that the constant 2-stack with fibre C (a 2-groupoid) is the classifying object for locally constant stacks with fibres from C.

    I would add one caveat, however, that we only need fibres that are equivalent to discrete n-/oo-groupoids, but this is nitpicking.

    Also, under your 'toy version' heading, you have hit the nail on the head, but not at the angle I like ;) I don't believe that objects such as covering spaces should come equipped with trivialisations - they should be postulated to exist. When defining the category of covering spaces one doesn't take into account trivialisations, but just treats it as a full subcategory of a slice category. I shouldn't complain, because your covering spaces defined above are just anafunctors 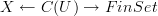X \leftarrow C(U) \to FinSet from the Cech groupoid of an open cover 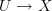U\to X, and I like anafunctors.

    I suppose I would like to see some sort of reconstruction, along the lines of the Wirth-Stasheff paper, of a 'total space' from the presheaf/anafunctor (which is really just a homotopy coherent cocycle). In fact, I've been meaning to think about the axioms presented in that paper in the context of (oo,1)-categories, either myself or convince you to bring your newfound expertise to the table.

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    I'm impressed! This is precisely what Polesello-Waschkies prove for locally constant stacks,

    Yes, I have read the article now. It is a very nice article. But I alsways have that urge to make the picture look even simpler by making it more abstract. I have just added their reference with a bit of discussion of how one may think of their results as fitting into the very abstract picture that I describe atlocally constant oo-stack -- References. Please have a look.

    From what I write there you can see that the suggestions would be that their result should have a considerbale strengthening, even if we stay with 2-stacks on Top. Namely they prove the adjunction 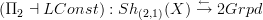( \Pi_2 \dashv LConst) : Sh_{(2,1)}(X) \stackrel{\leftarrow}{\to} 2 Grpd that should exist globally on the left only on representables.

    I don't believe that objects such as covering spaces should come equipped with trivialisations - they should be postulated to exist.

    Sure, I know what you mean. But see, all did was to indicate the computation of the stackification of 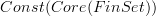Const (Core(FinSet)) and it so happens that I can compute stackifications best in terms of the +-construction, which is what I did. But the resulting stack is of course equivalent, then, to the more intrinsically defined one, where you just say it assigns the groupoid of covering spaces (defined your favorite way) to a given test space. But somehow I have to prove that this is the stackification of what we started with! I did this using covers, but that's just the computation, nothing of intrinsic meaning.

    I suppose I would like to see some sort of reconstruction, along the lines of the Wirth-Stasheff paper, of a 'total space' from the presheaf/anafunctor

    I might have to have another close look at their article. But my impression is that there is a clear general algorithm: the total space is the homotopy fiber of the classifying cocycle/anafunctor, whatever you call it.

    • CommentRowNumber20.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 5th 2010
    The existence of a mapping cylinder, used for the gluing together, is the tricky bit (see discussion in the article), but perhaps the homotopy fibre is enough. Not sure how that works for the homotopy cocycles there, but will think about it.
    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010

    Okay, I need to remind myself of what they do.

    But given my experience, I am inclined to say: if their total space is not the homotopy fiber of the classifying map, then this is not the fault of the homotopy fiber. If you see what i mean.

    • CommentRowNumber22.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    I think I see now how Toen does implicitly produce the equivalence between locally constant oo-stacks on X and functors 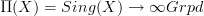\Pi(X) = Sing(X) \to \infty Grpd after all. Above I said that it seems as one needs one more step on top of his result but it's really an obvious step:

    he proves an equivalence between fibrations of simplicial sets over 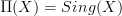\Pi(X) = Sing(X) and locally constant oo-stacks. theorem 2.13, page 25.

    But Quillen-fibrations 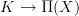K \to \Pi(X) between Kan complexes are Cartesian fibrations (as now recalled there) and the oo-Grothendieck construction says that these are equivalent to oo-functors \Pi(X) \to \infty Grpd.

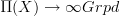    So slightly implicitly, Toen does prove an equivalence

    LConst(X) \simeq Func(\Pi(X), \infty Grpd)

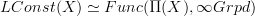
    between locally constant oo-stacks on X and representations of the fundamental oo-groupoid on oo-groupoids.

    Am I not right? On p. 32 of their article Polesello and Waschkies make some remarks to the extent that Toen's work would sort of go in this direction somehow, but not quite achieve this. But to me it looks as if he does achieve precisely this.

    But maybe I am overlooking something. Comments are welcome.

    • CommentRowNumber23.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    I have typed the above argument into the section Locally constant oo-stacks on topological spaces.

    Please have a critical look.

    • CommentRowNumber24.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    Just discovered that Mike has an article on essentially the same statement as Toen's : Parameterized spaces model locally constant homotopy sheaves

    Leaves me a bit puzzled that this wasn't mentioned in our discussion before. But okay, all the better.

    • CommentRowNumber25.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    Urs, it is not Toen who went first to go for a homotopy groups via Tannakian reconstruction, namely this is one of the MAIN and explicit topics and the motivation of Grothendieck's 1983 Pursuing stacks. For Grothendieck and every algebraic geometer since his works in 1960s, the fundamental group is the one which is Galois, i.e. the group of deck transformations in the suitable generalization of coverings. In 1980s Grothendieck wants to do this with higher groupoids. This is pursuing stacks. If you want to do homotopy groups and not homotopy groupoids OK. In any case, the Tannakian reconstruction is the procedure to get the automorphisms of the appropriate fiber functor.

    I myself was interested how this fits with Galois descent. In 1-categorical situations, Galois descent and equivariant descent of equivariant qcoh sheaves along torsors ar two special cases of Hopf Galois descent (in affine situation) so I wanted to understand equivariant descent of object along 2-torsors. This makes sense for internal groups in the base 2-category of 2-fibered category and a theorem holds if the latter is 2-stack and we have a 2-torsor internally downstairs. I gave a talk at Vienna in 2006 (I think you were there) partly about this work. The motivation was to possibly say something about homotopy 2-type of a scheme, in easy way, without full theory of Voevodsky. Bit this was just the tiny piece of the program and I did not understand some other things in the setup. In any case, Ijust want to say that you are right in your picture of the role of Tannakian formalism etc. and that the ideas are not new, but technically things with higher Tannaka etc. are more or less unfullfilled, and Toen's works are big steps forward technically.

    1-categorical situation is also not fully known. Namely it is OK in good categories, say for toplogical spaces and etale site in algebraic geometry, but there are wider classes of 1-categories where the algebraic approaches can lead to appropriate notion of fundamental group, without having structure to do homotopy theory. For example, work of Pataraia has been motivated by this. Some people tried to look for fundamental groupoid in Connes' nc geometry, but it is not finished satisfactorily to my knowledge.

    • CommentRowNumber26.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 5th 2010

    I think I have notes from your 2006 Vienna talk, Zoran. I'll have a look at home tonight.

    • CommentRowNumber27.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    The fiber functor discovered by Grothendieck in his Tannakian formalism has its name exactly because of the picture with universal covering spaces: the automorphisms of the FIBER are the deck transformations. If one takes a point in the base and attaches to it a fiber over it and takes its automorphisms that is the fundamental group in that point. The deck transformations are in a sense the automorphisms of the point. Namely each point knows the fiber of its universal covering spaces. Thus the group of deck transformations, is in a sense an automorphism group of a point. Infinitesimal loops around a point are its internal automorphisms, they LIFT via monodromy to deck transformations. This picture is almost in the same words (in my memory) described in Cartier's beautiful paper "Mad day..." on concepts of a space. He then alludes to the same situation internally to a topos. But one can go to some extend even if you are not in a topos...some weaker situations apply (not counting categorifications).

    • CommentRowNumber28.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    I found it now, but have no time to check, I need to get a bit of sleep...

    Pierre Cartier, A mad day's work: from Grothendieck to Connes and Kontsevich The evolution of concepts of space and symmetry, Bull. Amer. Math. Soc. 38 (2001), 389-408.

    http://www.ams.org/bull/2001-38-04/S0273-0979-01-00913-2/S0273-0979-01-00913-2.pdf

    • CommentRowNumber29.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 5th 2010

    You must do - I've been keeping an eye on the time in Croatia!

    • CommentRowNumber30.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    I added the discussion above into idea section at the begining, it could be more appropriately merged. We need more work on entries related to Tannaka reconstruction and very related fundamental group of a topos. It would be also good to look at Pataraia

    • D. Pataraia, Internal categories in the left exact cosimplicial category. Georgian Math. J. 4 (1997), No. 6, 533-556. (link)
    • CommentRowNumber31.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    I should also say that though it has been a single effort of Grothendieck two different aspects are now called Grothendieck's Galois theory. One is this general method of looking at Galois theory from geometrical viewpoint. Another is the very statement of classical Galois correspondence. Grothendieck's Galois correspondence is simply the correspondence between G-sets and appropriate class of "separable algebras". The pro-finite topology related to the Pierce spectrum (which is a very naive kind of spectrum using soberifcation, much more naive than the ones in nc geometry) plays a major role. This setup generalizes in categorical Galois theory of Janelidze.

    • CommentRowNumber32.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    Urs, it is not Toen who went first to go for a homotopy groups via Tannakian reconstruction,

    Well, but he seems to be the first who have realized the idea and proved the expected result. But the entry homotopy group of an infinity-stack does say that

    The general idea is that of Grothendieck's Galois theory.

    Maybe we should highlight this more. But then, I have come to think that the construction of homtopy groups as automorphisms of the fiber functor from locally constants stacks is not the central aspect of the situation. For instance Polesello and Waschkies prove their result for 2-stacks without this. What seems to be crucial is the realization that the fundamental oo-groupoid

    \Pi : Sh_{(oo,1)}(C) \to \infty Grpd

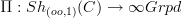
    is, at least on some objects, right adjoint to forming locally constant sheaves

    LConst : \infty Grpd \to Sh_{(\infty,1)}(C) .

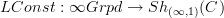    This is what these articles actually show.

    I think that's also a nices in that this produces the full fundamental oo-groupoid instead of just its loop space objects 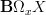\mathbf{B} \Omega_x X at a given point.

    • CommentRowNumber33.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    Of course Toen has done something new and technically awesome, but in Grothendieck's manuscript there are tens of pages of constructions related to this idea (it was not just idea, he wrote hundreds of details) and there is another several hundered pages of a manuscript on Galois theory he wrote few years later. You see, even the fact that Grothendieck had all the details of a version fo Batanin's definition of n-categories written for n-groupoids but straightforwardly can be written for n-categories, has not been realized until Maltsioniotis studied carefully his manuscript. You tend to like references written after 2000 which of course clean up the old ideas, but historical assertions do not mind unpolishedness in original works (many of which are usually, if it is about something radically new, unpublished).

    Zoran

    • CommentRowNumber34.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010

    You tend to like references written after 2000 which of course clean up the old ideas

    That may be right. Life is short.

    But please, let's add histroical accounts to entries where necessary. I don't know what it is I said or wrote that made you start pointing to Grothendieck.All I meant to do in the above was to point out what exactly Toen proves in his article.

    Which is, by the way, less than I expect can be proved. Maybe Grothendieck, too talked about this: all the articles listed above, Toen, Waschkies, also Mike's, they look at homotopy groups of ordinary topological spaces in terms of locally constant oo-stacks on them.But what we really are heading for is the analogous definition for homotoppy groups of oo-stacks on topological spaces So so far these references just concern the representable objects.

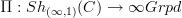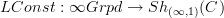    I think that quite generally we should have that left adjoint \Pi : Sh_{(\infty,1)}(C) \to \infty Grpd of LConst : \infty Grpd \to Sh_{(\infty,1)}(C) . That's what oo-Galois theory should be all about.

    • CommentRowNumber35.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    What maid me pointing ? look you wrote:

    The basic idea for 1-sheaves is Grothendieck's, for oo-stacks on topological spaces it has been clarified by Toen.

    This sentence cries for interpretation that Grothendieck saw just the 1-categorical case and he did not have the infinite categorical version clear !! He did not care to prove qall the lemmas but he had clear all the assertions and uqite much about what is the natural technology behind it.

    • CommentRowNumber36.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    In my memory, the categorical Galois theory also has to do with some adjoint pair, but I am not sure if it is the anloague of what you talk about.

    But please, let's add histroical accounts to entries where necessary.

    I done it many times, and it is easy when nothing is written or what is already written is true. But once the wrong historical theories are present it takes me a lot to take a stance, explain to others and rewrite it. I wrote a number of things which I know from conversations with older mathematicians etc. of course there are errors but still I care that there is some info behind and not the result of comparison of abstract of one 1965 paper and reading one 2000+ paper. Conservativeness in writing historical notes makes it time-saving in the long run I think.

    • CommentRowNumber37.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010
    • (edited Feb 5th 2010)

    What maid me pointing ? look you wrote:

    The basic idea for 1-sheaves is Grothendieck's, for oo-stacks on topological spaces it has been clarified by Toen.

    I see. Sorry, I had no idea that you were referring to this sentence. That is from the very first message here in a long thread, right? :-)

    I have tried now to make this clear and set this straight by creating a section

    Homtopy group of an oo-stack -- History

    Please have a look.

    • CommentRowNumber38.
    • CommentAuthorzskoda
    • CommentTimeFeb 5th 2010

    Maybe one should find out what Lurie has in this direction in HTT. I think he has soemthing as well there.

    • CommentRowNumber39.
    • CommentAuthorUrs
    • CommentTimeFeb 5th 2010

    Maybe one should find out what Lurie has in this direction in HTT. I think he has soemthing as well there.

    Could you check that? I haven't read all of section 7 yet. In section 6.5 he discusses the categorical homotopy groups. I don't think thaat I have seen the geometrical ones discussed by him. But could be that I missed it.

    • CommentRowNumber40.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    ...

    • CommentRowNumber41.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 22nd 2010

    I have been checking back on this thread which I had neglected for some reason that I do not understand. Zoran some time ago said

    You see, even the fact that Grothendieck had all the details of a version fo Batanin's definition of n-categories written for n-groupoids but straightforwardly can be written for n-categories, has not been realized until Maltsioniotis studied carefully his manuscript.'

    That is not correct! My problem throughout this story is that I had read Grothendieck and understood what he said! In some way this blocked me from trying the overarching derived stack theory as a way out, shying away from the 'nitty-gritty'. For instance, I have always asked myself what should be 2-Galois theory and wanted to have the possibility of a theory that also had the other features that AG seemed to be identifying. A lot of the story that we wanted and 'saw' is still not there.

    As elsewhere David says, we need both a top down and a bottom up approach. For instance, I give you a 3 manifold and I want a construction from it of a 2-covering space, so that I can do 'categorified analogues' of ALL the usual low dim. topology of covering spaces of surfaces. I think general categorical constructions are in the literature and David has gone a lot further than most in pushing these through in the detail we both would like, but I do not know of a published version which, say, is an attempt to show by elementary means that a `universal' such gadget exists. I had a tentative construction early on using the topologised singular complex, (I remember talking to Fred Linton about it in Bangor in ?1984?), but no one seemed interested at the time so I never worked it up to see if all the gory details worked. (When I say I do not know, please note that is a statement of my ignorance nothing else!)

    • CommentRowNumber42.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010

    Maltsiniotis gave a talk in Barcelona saying exactly what I am saying above; Joachim Kock, and some other people confirmed his reasoning; Batanin was present. I don't believe anybody understood the whole over 500 pages of the P. Stacks manuscript plus several hundred pages of the second, bit later, manuscript on Galois theory (travaux...).

    • CommentRowNumber43.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 22nd 2010

    Sorry Zoran, I was not making quite the point that you are referring to and clearly I was less than clear. I do not claim to have understood the whole of the PS as there are bits of Algebraic Geometry that as very obscure to me and my intuition for them is very weak. The initial steps for the n-groupoid approach were sketched out, if I remember rightly, not in PS but in the letter to Larry Breen. I was reading and reacting to the manuscript as it arrived in Bangor, and was feeding back impressions and comments to Grothendieck initially through Ronnie Brown and then directly.

    When Michael Batanin produced his construction, it seemed to me to be highly original, adapting work that he had done in Strong Shape and in discussions with Cordier in Amiens, with ideas that were essentially in those letters and manuscript of Grothendieck as well as constructs and expertise from the Australian school of category theory.

    That is history, and we should not worry too much about it except for where it points out things for us to clarify and to fill in the gaps.

    I still maintain that in the incredible work done recently on this area there is quite a lot of 'bottom up' still to do if we are to bridge the gap between this very high powered stuff and the work of the non-n-cat mathematician. (I think I remember that somewhere in PS Grothendieck say he hoped that there would not be a need for an idea of a higher dimensional topos as he felt the topos idea was so pretty, yet that is the way people have got around the problem. Perhaps that is again the bottom up approach being desired.)

    • CommentRowNumber44.
    • CommentAuthorAndrew Stacey
    • CommentTimeFeb 22nd 2010

    (The spam post that Urs refers to 4 posts back has been removed from public view and the account used to post it set to "banned".)

    • CommentRowNumber45.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010

    he hoped that there would not be a need for an idea of a higher dimensional topos as he felt the topos idea was so pretty

    But the notion of (oo,1)-topos is even prettier! I keep being amazed at how pretty indeed it is, as exhibited for instance by all the structures in an (oo,1)-topos that exist canonically.

    And one can see that much of classical topos theory was really a hack to get this nice oo,1-picture. everything people did with simplicial objects in a topos is a hack for the corresponding (oo,1)-topos.

    And this involves notably the Galois theory. I have tried to substantiate this claim with all the references now commented and collected at homotopy groups in an (infinity,1)-topos.

    • CommentRowNumber46.
    • CommentAuthorTodd_Trimble
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> But the notion of (oo,1)-topos is even prettier! </blockquote> <p>A matter of taste?</p> <blockquote> And one can see that much of classical topos theory was really a hack to get this nice oo,1-picture. </blockquote> <p>That sounds like an extremely revisionist point of view. Which parts do you think were "hacks"?</p> </div>
    • CommentRowNumber47.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    Which parts do you think were "hacks"?

    Everything involving simplicial objects in a topos. The category of simplicial objects in the topos may be seen to be a model for the corresponding (oo,1)-topos.

    Homotopy groups in a topos were classically defined in terms of colimits over simplicial objects in that topos. That colimit serves to pick the cofibrant objects in there and to compute the right (oo,1)-categoriecal hom-spaces.

    I think this not only gives an aesthetically more pleasing picture, it also helps to gain insights: originally homotopy groups in a topos were defined in the method by local contractions for every locally connected topos. Then Artin-Mazur showed that this gives the right homotopy groups for a topological space only if that is locally contractible. The (oo,1)-perspective explains what's going on: generally the method of computing homotopy groups by this method requires that the corresponding (oo,1)-topos is a locally contractible (infinity,1)-topos.

    • CommentRowNumber48.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010

    One can have two sites which produce equivalent 1-topoi of sheaves, but nonequivalent 2-topoi of 1-stacks. Regarding that the simplicial objects in the topoi can yield cohomological information, then there is a different cohomological information in the choice of a possible 2-topos in such cases. How does one reconcile this mutliplicity of cohomology classes by using infinity topoi ?

    • CommentRowNumber49.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 22nd 2010

    Put that way and reminding me of Artin-Mazur, then we might reasonably expect the general case (of a (\infty,1) corresponding the a non-locally contractible situation to have some (possibly distant) link with the (strong) shape homotopy groups, which is what I have always hoped for. So start with a general compact metric space and the (\infty,1) -topos constructed by simplicial sheaves (?), how does one calculate the homotopy groups, and how do they compare with the Borsuk shape theory fundamental shape groups etc. of the space. This is not just idle questioning, as there are numerous cases where the shape of a spectrum in functional analytic problems gives the necessary insight, similarly from KK-theory and similar contexts. There are perhaps indications from non-commutative geometry that the non-com. C^* algebras can be similarly studied. (I know that is vague... but I have not discussed this with people lately so do not know current state of play.)

    • CommentRowNumber50.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    How does one reconcile this mutliplicity of cohomology classes by using infinity topoi ?

    Using simplicial objects in a topos with equivalences given by stalkwise acyclic homotopy equivalences of simplicial sets (as in the references I linked to) produces the Hom-spaces in the hypercomplete (infinity,1)-topos over any site for the topos, provided that topos has enough points.

    • CommentRowNumber51.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    @Tim:

    I think the discussion and references at homotopy groups in an (infinity,1)-topos shows that:

    given a locally n-connected (n,1)-topos, the left adjoint 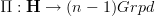\Pi : \mathbf{H} \to (n-1)Grpd produces the same homtopy groups as obtained from Galois theory of locally constant (n-1)-stacks.

    As we have seen there, this follows from just the (n,1)-Yoneda lemma as soon as we realize that the n-stack of locally constant (n-1)-stacks is just the constant n-stack on 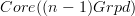Core((n-1) Grpd) . That this is the case for low n as compared to independent definitions is in the Waschies et al. article.

    If the topos is not locally k-connected above some 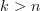k > n then the definitions of homotopy groups will begin to diverge.

    • CommentRowNumber52.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 22nd 2010

    One can have two sites which produce equivalent 1-topoi of sheaves, but nonequivalent 2-topoi of 1-stacks.

    I was not aware of that, nor do I understand how it can be true, since the 1-topos contains all of its sites as generating subcategories, so it seems that a stack on any of its defining sites should be the same as a stack on the big site of the topos itself. My understanding is that the issue of hypercompleteness only arises once you get all the way to the oo-world. Can you give an example and/or reference?

    • CommentRowNumber53.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    @Urs I accept that but feel that somehow there is a deficiency in the theory if we cannot approach moderately grotty non locally connected spaces such as the Warsaw circle or limit situations like the solenoids. (Especially these later as they are related to strange attractors etc. and it would be interesting to push this theory of (oo,1)-toposes to look at the geometric style invariants of such spaces. I am probably hoping for too much.)

    • CommentRowNumber54.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010

    @Tim: you can consider the definition of homotopy groups based on monodromy in every (oo,1)-topos. All I am saying is that it will coincide with "the other definition" only under additional assumptions.

    I'd be glad to learn more about what happens in situations that do not satisfy the various conditions used at homotopy groups in an (infinity,1)-topos, such as locally contractible, paracompact, etc.

    • CommentRowNumber55.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    @ Zoran and Mike,

    yes, so as we discussed last time elsewhere, if an object satisfies Cech descent, then it already satisfies descent over all bounded hypercovers. If the object is itself truncated, then that means it satisfies descent over all hypercovers. So a difference appears only for untruncated objects, i.e. genuine oo-stacks. For these, one finds examples that satisfy Cech descent, but not hypercover desent (as in the appendix of Dugger-Hollander-Isaksen).

    But useing general simplicial objects in an ordinary topos means admitting untruncated oo-stacks. So it is a reasonable question to ask which corresponding (oo,1)-topos is implicit in classical topos theory. And since usually the stalkwise weak equivalences are used, the answer is: it is the hypercomplete version. If the underlying topos has enough points. (If it doesn't have enough points, then i am afraid the classical definition has no really good meaning.)

    • CommentRowNumber56.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    Urs I did not understand your answer 50. I you are given a Gorthendieck 1-topos of 1-sheaves and Grothendieck 2-topos of 1-stacks, what is the infinity topos produced from these choices as opposed to the old Grothendieck case where I have just 1-topos and simplicial object inside ?

    This should also lead to some intrinsic consistency condition on which 2-topoi are compatible with the 1-topos chosen (classically it means there is a site which can afford both initial data are structures over it, but this is not intrinsic) ?

    Mike said

    I was not aware of that, nor do I understand how it can be true, since the 1-topos contains all of its sites as generating subcategories, so it seems that a stack on any of its defining sites should be the same as a stack on the big site of the topos itself.

    This is in Giraud, in my memory about page 98.

    • CommentRowNumber57.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010

    what is the infinity topos produced from these choices as opposed to the old Grothendieck case where I have just 1-topos and simplicial object inside ?

    If the topos is a sheaf topos, then simplicial objects in it are of course just simplicial sheaves. There are different model category structures on simplicial sheaves. Some represent hypercomplete (oo,1)-toposes, some not. But if the topos has enough points and if one takes the weak equivalences between simplicial sheaves to be stalkwise weak equivalences, then this amounts to producing the corresponding hypercomplete (oo,1)-topos.

    • CommentRowNumber58.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 22nd 2010

    Sorry, what reference is "Giraud"?

    • CommentRowNumber59.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    Sorry, what reference is "Giraud"?

    Cohomologie non-abelienne

    • CommentRowNumber60.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    I am asking about THESE choices, NOT the Grothendieck case. You are giving me repeatedly the obvious answer about the classical Gorthendieck case. I am asking about the puzzling case (I used to ask you about that still in Bonn but I assume you now know the answer), where a nonstandard choice for 2-topos is taken, that is not the stacks in regular epimorphism topology but the stacks on an arbitrary chosen site given the 1-topos. So 1-topos AND 2-topos are given.

    Mike: Giraud's book

    • CommentRowNumber61.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010

    Zoran,

    I am sorry for not getting your point. Maybe I still don't get it. You write:

    but the stacks on an arbitrary chosen site given the 1-topos.

    What do you mean by an "arbitrary site given a 1-topos"? Or do you mean just any arbitrary site? I am confused!

    It seems to me that the important point is the one we mentioned before, that for finite n, there is only one localization of n-presheaves on a site that is a "usual localization".

    More precisely, by "usual localization" I mean what in HTT is called "topological localization" and the precise form of the statement is proposition 6.4.3.9 there.

    I suppose you are asking about "non-usual localizations". In which case I am probably out of my depth. I have as yet very little feeling for n-toposes that do not arise by "topological localization".

    Anyway, in order to prepare the ground for further discussion, I will quickly create an entry topological localization.

    • CommentRowNumber62.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    As I wrote in the first message in this chain we can have two different choices of sites which give the same 1-topos of sheaves but different 2-topos of stacks. If I start with a topos, it is USUAL to talk about stacks in regular epimorphism topology. This corresponds to a particular choice of a site producing that topos. This is usual and default choice in topos theory. But it is not necessary. One can take another choice of site, and Giraud claims that it is not necessary that the 2-topos of Grothendieck 1-stacks on that site is equivalent to the 2-topos on the regular epimorphism site.

    I will look at your entry, but the question is simple and non-technical.

    Edit: I do not know if the nonequivalent sites still appear if we just look at stacks in groupoids, but I would guess it is not essential. I can not find the exact assertion in the Giraud book file at the very moment.

    • CommentRowNumber63.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 22nd 2010

    In Remarque 3.3.4 on p93 of "Cohomologie non-abélienne" I read

    On résume (3.3.3) en disant que, par image directe et inverse, la donnée d'un champ sur 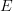E équivaut à la donnée d'un champ sur le topos associé \tilde{E}.

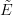    which I translate as

    We summarize (3.3.3) by saying that, via direct and inverse image, to give a stack on 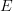E is equivalent to giving a stack on the associated topos \tilde{E}.

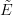    This is what I was saying before. If giving a stack on a site E is equivalent to giving a stack on the associated 1-topos, then two sites having equivalent 1-topoi of sheaves cannot have inequivalent 2-topoi of stacks.

    • CommentRowNumber64.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    Ohh, I just saw your last comment. Of course, if you look at a topology on the 1-topos other than the canonical one, then you'll get a different notion of stack. But I don't think it makes sense to call those stacks on some site defining the 1-topos. Stacks for some random topology J on a topos E are just that, stacks for the topology J on E. In general, there is no site whose 1-topos of sheaves is E but whose 2-topos of stacks is the topos of stacks for J on E.

    Edit: Clarified, since I'm not sure if by "regular epimorphism topology" you meant the canonical topology, or the topology generated by singleton (regular) epimorphisms.

    • CommentRowNumber65.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010
    • (edited Feb 22nd 2010)

    I went last year to read 3.3.1 by a rather reliable reference which claimed that Giraud has 2-fully faithfulness in that proposition, and that the equivalence does not hold (I needed equivalence at that time for my purposes). Now you prove me and my informant to be wrong, what I found still strange as I vividly recall seeing the statement to the opposite and thinking of that the whole evening afterwards.

    As far as other topologies on the topos you are right I have been misinterpreting their role above. Maybe that is what I was thinking at the time. But this has no repercussions for Urs-s point of view as this is just another 1-topos behind the picture (to emphasise your clear and obvious remark: In general, there is no site whose 1-topos of sheaves is E but whose 2-topos of stacks is the topos of stacks for J on E).

    2nd edit: thanks Mike. I think I reconciled most by now, at least with Urs's point of view if not with history of my misunderstanding.

    • CommentRowNumber66.
    • CommentAuthorUrs
    • CommentTimeFeb 22nd 2010

    okay, I need to catch up with your discussion here. Meanwhile I wrote topological localization. I understand that this is not what you, Zoran, had in mind, but maybe it is useful for something anyhow.

    • CommentRowNumber67.
    • CommentAuthorzskoda
    • CommentTimeFeb 22nd 2010

    Don't spend time on what I had in mind, only trivial things mistified by my own confusion&memory.

    • CommentRowNumber68.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 23rd 2010
    @Tim,

    how does one define strong homotopy groups? We could do with a page on this :) Also I have some ideas on showing universality, but as someone once said, I had to leave something to do afterwards. Also, there is a general construction for functorial n-connected covers going through sSet and using coskeleton and decalage and back to Top, but it's hopeless to do any geometry with it, as it is \'as big as\' the geometric realisation of the singular complex of the space in question. My personal hope is that we can rather get something like a topological Trimble n-groupoid model for n-connected covers, but it is at the moment beyond my (rather meager) n-categorical skills.
    • CommentRowNumber69.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 23rd 2010
    Speaking more generally, we haven't considered what sort of fibre functor these n-covering spaces come with. There was some early emphasis on finite fibres on the page in question, possibly misplaced, but this sort of thing needs to be examined in the light of (strong) shape theory. I suppose in general, homotopy groups will be pro-groups, not necessary pro-finite groups.

    Obviously the end result should be an n-groupoid, but for now we can focus on the case of a pointed space and look at the autoequivalences of the fibre functor. The trick (and it's a big trick) is to show that these autoequivalences form a pro-n-group.
    • CommentRowNumber70.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 23rd 2010

    @David: I'm not sure what you want from 'strong homotopy groups'.

    I am getting confused again. The homotopy groups (of whatever strength (:-)) are perhaps not really what we need. If you asked for small models of the strong 2-type I would still not know what you wanted but would feel happier!

    • CommentRowNumber71.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 23rd 2010
    • (edited Feb 23rd 2010)

    Ah, I'm sorry. At some point you (Tim) wrote

    how do they compare with the Borsuk shape theory fundamental shape groups etc. of the space.

    so I think I meant 'fundamental shape groups'.

    Having a read of some shape theory stuff yesterday reminded me how it all came about. In that case, let me go back a step: is there, for the theory of strong shape, an n-truncation procedure for each n, as there is for homotopy types (or even Postnikov towers)? Is there also a co-truncation, i.e. Whitehead towers?

    • CommentRowNumber72.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 24th 2010

    According to the original descriptions of strong shape (or at least those that were nearest the methodology we are using here), which came from Edwards and Hastings at about the same time as I was looking at a very similar theory, the approach was by localising pro-SS with respect to some levelwise weak equivalences (suitably closed up under retraction). This was the ambient category in which things lived. You then took spaces and applied the Vietoris complex construction to get to pro-SS. The strong shape of a space was the isomorphism class of the resulting object in Ho(pro-SS). In the stuff for that time there were various approaches to doing Postnikov etc. I cannot be sure they were all that good and they need at least a glance to check. I had used a slightly different approach to Ho(pro-SS) adopting a BrownAHT with minor modifications. (The paper is linked to from the shape theory page.) There was a second paper giving related homological results then a third doing an obstruction theory. My memory is that that used Postnikov towers. Whitehead towers I seem to remember were much more tricky for my methods so ??????

    Beware Edwards and Hastings produce some neat examples where things that are not as simple as you might think!

    Another point with their work is that it introduced proper homotopy theory in a new way and THAT is I think an important potential application for the new insights and methods. The application would need quite a lot of working through to interpret the results in a way meaningful to the sort of questions that need answering and might impact on non-compact manifold theory in a neat way. I do not know and will not attempt to work it out here!

    • CommentRowNumber73.
    • CommentAuthorUrs
    • CommentTimeFeb 24th 2010
    • (edited Feb 24th 2010)

    adopting a BrownAHT with minor modifications. (The paper is linked to from the shape theory page.)

    Just a technical comment: you can just include the keyword here in double brackets as on the nLab and the software will automatically create a link: BrownAHT

    • CommentRowNumber74.
    • CommentAuthorUrs
    • CommentTimeFeb 24th 2010

    more on topic: it would be nice if all such technical details could eventually be mentioned at shape theory.

    For instance statements such as

    The strong shape of a space was the isomorphism class of the resulting object in Ho(pro-SS)

    should go in the Definition-section in the section "Shape theory for topological spaces".

    • CommentRowNumber75.
    • CommentAuthorTim_Porter
    • CommentTimeFeb 24th 2010

    One of my THINGS TO DO is to set up a Strong Shape Theory entry and to migrate some of the stuff and references from Shape to there. (There are only 48 hours in the day and 9 days in the week however... as someone said!) :-)

    • CommentRowNumber76.
    • CommentAuthorUrs
    • CommentTimeFeb 24th 2010
    • (edited Feb 24th 2010)

    There are only 48 hours in the day and 9 days in the week however... as someone said!

    sure, I know this well. Please don't read my comment as pushing you to do more work. On the contrary: I am just thinking that if you take the time anyway to drop hints here in the forum, then that time is used more efficiently by dropping these hints into the relevant nLab entry and then linking to it.

1 to 76 of 76

  1.