nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 5th 2010
I guess this is well known, but let me try writing it here and see what happens.
If a connection on a principal -bundle is locally represented by the 1-form with values in , then the connection is flat if and only if the curvature 2-form vanishes, that is, if is a solution of the Maurer-Cartan equation.
Now, what is interesting is that one can see curvature only on 2-dimensional paths (it is a 2-form): if one restricts to a 1-dimensional submanifold, then there is clearly a solution to the Maurer-Cartan equation. so, if I think of an infinitesimal 1-simplex and look at my connection there, I could say that my connection is 1-flat. then, moving to an infinitesimal 2-simplex I see that the connection is (generally) not 2-flat: holonomy along two sides of the 2-simplex is not the same thing as holonomy along the third side. not the same, but in a very precise way: the curvature exactly measures the gap to go from a horn of the 2-simplex to the third edge. this is very 2-categorical, and suggests I could cure the lack of flatness of my original connection by adding a copy of in degree -1 and cooking up a 2-Lie algebra . Maurer-Cartan equation for this 2-Lie algebra would coincide with the original one one the 1-simplex (since only degree 1 elements are 1-forms with values in . but on the 2-simplex we would have, in addition to these elements, also 2-forms with coefficients in , and the Maurer-Cartan equation on teh simplex would look like where is the differential of the -algebra (and it should be induced by the identity of , thought as a degree 1 map from to ). So the original equation telling that had curvature is now equivalent to say that is flat.
in other words, what seemed a non-flat connection was so since I was not seeing the 2-bundle, but only a 1-bundle approximation. and on a 1-bundle I can only clearly see up to 1-simplices, wher my connection was actually flat.
once curvature has come in, we can repeat the argument: now we have a 2-flat connection and test it on the 3-simplex. if it has 3-curvature, that will presumibly be because we are not seeing the 3-bundle, yet. so I find it natural to wonder (to conjecture) whether any connection on a principal bundle (and more generally any -flat connection on an -bundle) can be seen as a flat connection on an -bundle. -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
Hey, that's exactly the right idea! This is the way to go.
What you are describing can be said like this:
for
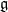 an
an 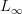 -algebra, a flat
-algebra, a flat 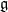 -valued connection (on a trivial bundle) is a morphism of oo-Lie algebroids
-valued connection (on a trivial bundle) is a morphism of oo-Lie algebroids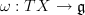
we may integrate this to a morphism of oo-Lie groupoids, where it becomes
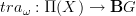
where G is the oo-group that integrates
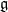
we can make this non-flat precisely the way you describe: we describe a flat connection with coefficients in something one degree higher. That thing is the mapping cone on the identity on
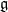 , which is a Lie (n+1)-algebra
, which is a Lie (n+1)-algebra 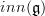 if
if 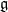 was a Lie n-algebra.
was a Lie n-algebra.So a non-flat
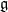 -connection is a locally a flat
-connection is a locally a flat 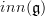 -connection,
-connection,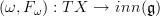
There is, to my mind, a beuatiful story developing from this point. This is, incidentally, the story that I am trying to develop on my personal web. :-)
Directly addressing your remark is for instance the entry curvature of oo-Lie algebroid valued differential forms. This sits in a bigger story of a full theory of higher connections, as you can find out by walking around the links provided there.
I'd be happy to talk about this stuff more. That's nice. I am enjoying how you recently kept addressing various points that I am very intested in.
-
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
well, it's not so surprising I'm currenly on the same tune as you.. the flat connections stuff above originated from you explained me about the d'auria-fre formulation of supergravity :-)
I've now been through curvature of oo-Lie algebroid valued differential forms. I find there are too many banks of herrings swimming there (at least for my taste). I mean: you first define -valued flat connections. next you define -valued non-necessarily-flat connections, which, by the way are not -valued, but -valued. and this leads us to the quite weird notions of (my words, not yours) -valued flat-non-necessarily-flat, that is the -valued non-necessarily-flat connections which are induced by -valued flat connections.
so let us simplify this a bit: let us say that a -connection is (locally) a morphism . and that's it. then we say that an -connection is flat if this morphism factors through .
the only problem I see with this definition is that a classical -connection is not a connection.. but, as we argued above, a classical -connection is jus the shadow of a true -connection, so we could call it "preconnection". -
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
Thanks Domenico (#1), that just clicked for me now!
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeFeb 5th 2010
there are too many banks of herrings swimming there (at least for my taste).
Thanks for saying this, I am grateful for suggestions here.
I see what you mean. Yes, I should change that terminology maybe. I can't do it right now, though.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeFeb 5th 2010
Thanks Domenico (#1), that just clicked for me now!
I see. Would one of you mind writing a sentence or two then describing the situation in words that you think carry the message better? Like, into the Idea section of that entry on my page?
Sorry for asking this, but I just figured maybe I am saying it the wrong way all along and it comes across much better if somebody else says it.
-
- CommentRowNumber7.
- CommentAuthorTobyBartels
- CommentTimeFeb 6th 2010
At which page do you want that?
It's quite possible that you already wrote what, if I had read it as carefully as Domenico's comment, would also have made it click for me. But sometimes I don't read carefully everything that you write; there's too much of it for that.
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeFeb 6th 2010
- (edited Feb 6th 2010)
I am feeling a bit embarrased asking for this, but if you don't mind: I am thinking of the page curvature of oo-Lie algebroid valued forms
That needs more in the Idea-section anyway. Strictly speaking what I have there is a stub that I once wrote in a haste in reply to some blog discussion we had on Courant algebroids and the like. I will have to go over that page anyway.
I am also undecided as to how that page should sit besides the similar oo-Lie algebroid valued forms. Maybe I should merge both to one single page.
-
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 6th 2010
- (edited Feb 6th 2010)
I think I could take the task of working a bit on oo-Lie algebroid valued forms in the direction sketched above. yet, I'd like to still discuss it a bit here, sicne I'm now thinking of some more radical change. what I'm thinking is that the one-step definition as it is now is too strict. I mean, we are now defining flat -connections as a morphism , and then general connections as something which becomes flat in a single step, i.e., going from to . why should we restrict to this? it would be natural to consider thigs that become flat in 2 sterps, 3, steps, and so on. eventually we could have things which "become flat after infinity steps" (and by the way this vague notion seems to me to better fit with classical -connections).
let us see things the other way round: when we say flat, we mean flat in an -categorical sense, so let us stress this by saying that a morphism is an -flat connection with values in . then, what we are currently calling non-necessarily-flat -connections would be the -flat connections with values in . but starting from is not too practical.., let us start from 0 instead.
the one-step definition of non-flat connections is reflected in the one step going from the 0-groupoid to the -groupoid . but we have a whole tower of higher and higher groupoids in between: the -skeleta of . so we have
and we can talk of an -flat connection with values in as a morphism . this will not lift to a morphism unless the connection is -flat, but will lift to a morphism . the limit of this procedure will produce a "true connection" with values in .
I have a vague feeling that starting with a 0-falt -connection one will this way meet the series , , , , ,..., but I have to think more carefully to this. -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeFeb 6th 2010
- (edited Feb 6th 2010)
This is a very good point. I think I know what you mean only that I think that it is a bit more non-straightforward than it may seem. But maybe I am wrong about this. So let's see.
First, let me tell the story on how we ran into this originally, which sheds some light on the truncation business:
first we defined the 1-path goupoid
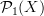 whose morphisms are thin-homotopy classes of paths, and proved that morphisms
whose morphisms are thin-homotopy classes of paths, and proved that morphisms 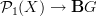 are ordinary
are ordinary 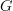 -connections, i.e. locally given by
-connections, i.e. locally given by 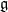 -valued forms.
-valued forms.Then at the beginning we thought the pattern should continue this way: we next defined the path 2-groupoid whose 1- and 2-morphisms are thin-homotopy classes of 1- and 2-paths, respectively. Then for
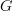 a smooth 2-group we thought a 2-bundle with connection should be a morphism,
a smooth 2-group we thought a 2-bundle with connection should be a morphism, 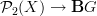 .
.But this showed a then unepected constraint: this is equivalent to "fake flat" 2-bundles, those for which the 2-form curvature part vanishes, and only the top 3-form curvature part may be nontrivial.
Back then this used to be a puzzle. Today I have understood what's going on. It is essentially what you just said:
We can think of
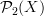 as a kind of truncation of
as a kind of truncation of 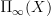 , where we have done 2 things:
, where we have done 2 things:thrown away all non-thin higher morphisms;
divide out the thin higher morphisms.
The fact that there are no nontrivial 3-morphisms in
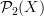 accounts for the fact that morphisms
accounts for the fact that morphisms 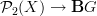 have no constraint in degree 3, hence may have non-vanishing 3-form curvature. But the 2-form curvature has to vanish, given by the fact that there are 2-paths in between 1-paths.
have no constraint in degree 3, hence may have non-vanishing 3-form curvature. But the 2-form curvature has to vanish, given by the fact that there are 2-paths in between 1-paths.Similarly, one can define path n-groupoids for higher n this way by throwing away non-thin higher morphisms and dividing out thin ones. And then for
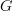 an n-group, morphisms
an n-group, morphisms 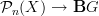 are given by
are given by 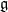 -valued form data where all the
-valued form data where all the 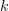 -form curvature connections have to vanish, except the one of degree n+1.
-form curvature connections have to vanish, except the one of degree n+1.We can get the fully unconstrained situation by instead looking at morphisms out of
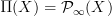 but with values not in
but with values not in 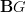 but in
but in 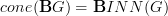 .
.However, I am not sure how one would systematically go about the hierarchical truncation that you seemed to suggest. Maybe think of it under the Dold-Kan image, where it is easier to see what is going on:
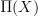 there corresponds to the deRham dg-algebra. What would you replace that with -- which other dg-algebra -- to get the desired truncation?
there corresponds to the deRham dg-algebra. What would you replace that with -- which other dg-algebra -- to get the desired truncation? -
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 6th 2010
- (edited Feb 6th 2010)
let me think... if we adopt the homotopy hypothesis (in a suitable strong sense), then we know which is the answer: the -groupoids will have to be equivalent to for some suitable space , and so the seeked for dg-algebras will be the de Rham algebras of . now, what is ? looking at its homotopy groups one sees that is the Postnikov system of . so what we really need here seems to be a smooth spaces realization of Postnikov systems. -
- CommentRowNumber12.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 7th 2010
- (edited Feb 7th 2010)
on second thought, we're clearly dealing not with the Postnikov system! our maps are going in the opposite direction! namely, we want
, whereas taking we would have
.
so, what is the series ? let us think to a discrete model to begin with, i.e. let be a simplicial complex. then we know what and should be: just 0- and 1-skeleton of . this hides a subtely: a 1-simplicial object is a . now let us take the next step. what if we take the 2-skeleton of as ? this surely has only thin -morphisms for , but it is not a 2-groupoid! yet, in working with differential forms it seems that the relevant notion is thinness rather than triviality: if is a map of differential manifolds which (locally) factors through a 2-dimensional manifold, then will pull-bak to no differential form on of degree higher than 2. so here we have to decide, and this decision will be crucial to the direction we'll develop this stuff: do we really want to be an -groupoid?
(at the moment I'm pending for: no, we'd rather develop a notion of thin smooth groupoid, and ask that is thin in degrees above , something we could call -thin) -
- CommentRowNumber13.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 7th 2010
- (edited Feb 7th 2010)
let me add something to this. in the path groupoid the notion of thin homotopy is precisely to kill 2-forms by pullback. on the other hand thin homotopy uses the cubical approach to homotopy, so taht it does not immediately generalizes to the path infinity-groupoid if we want to keep the simplicial description for it. but this is almost trivially cured: let us start with the path infinity-groupoid . Next we define the -thin sub-infinity-groupoid as the subgroupoid whose -morphisms are smooth maps which kill all differential forms on of degree greather than (this should be said in terms of the functor of points , but let us go with the naive idea for the moment).
with this definition we would have the seeked for sequence of infinity-groupoids
the groupoid is not an -groupoid; we could get an -groupoid out of it by truncation, but I'm not sure this is what we want to do: if is a Lie group, a -connection on a trivial -bundle could still be defined as a morphism , and the fact that is a 1-groupoid would ensure that this morphism factors through the truncation obtained by quotienting by thin homotopies.
then in going from 1-simplices to 2-simplices we see that there are two kind of obstructions ("true" and "fake" curvature?): namely there's an obstruction to extension , and an obstruction to truncation . if we are taking values in 2-groupoids, the second obstruction trivially vanishes.
the question: which dg commutative algebra corresponds to remains open, though I now suspect there could be an extremely simple answer: the quotient of the de Rham algebra of modulo the sub dg-algebra of differential forms of degree greater than . -
- CommentRowNumber14.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 7th 2010
- (edited Feb 7th 2010)
even better, every is an infinity-groupoid, so we can truncate it at every level , to get a -groupoid ,
and the 's fit into a big commutative diagram with maps and
. moreover, if , then , the -th homotopy groupoid of . in particular, for and we have the sequence of morphisms . given a 1-connection , for a Lie group , there's an obstruction to exending it to a 2-connection . once this obstruction vanishes, there is no further obstruction to factror through the truncation , since is a 1-groupoid. in other words, given a -connection , the obstruction for to give a morphism out of is the same as the obstruction for to give a morphism out of , and this accidental coincidence makes us confused when we have to decide what do we want higher curvature to be. -
- CommentRowNumber15.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 8th 2010
- (edited Feb 8th 2010)
in today's post (this entry is becoming a sort of blog... :-) ) let us go infinitesimal, and consider the infinitesimal version instead. on the (higher) Lie group side we find (higher) Lie algebras, so we end up with the following definition: locally a -connections with values in is a morphism . next we wonder whether we can extend this to an -connection with values in . by the above discussion what we can surely do is to extend to an connection with values in . so our original problem of extending becomes a problem of factoring: can we factor the map through ? the homotopy commutative diagram defining immediately tells us that an obstruction to factoring is given by the homotopy class of the composite map , i.e., by what Urs calls the curvature of in curvature of oo-Lie algebroid valued differential forms. in particular, when , i.e., one deals with -connections, the above discussion is reduces to Urs' definition of curvature characteristic form. -
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeFeb 8th 2010
- (edited Feb 8th 2010)
Hey Domenico,
thanks, that's great that you are thinking about this. I apologize for not having replied earlier. i was being distracted by other things, unfortunately.
I had had this co-tower
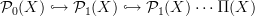 on my blackboard a few times with similar thoughts as you voice here, but somehow I never arrived at making some definite kind of statement.
on my blackboard a few times with similar thoughts as you voice here, but somehow I never arrived at making some definite kind of statement.You make some very good points here. Such that simplicially we obtain
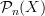 just by looking at the subset of
just by looking at the subset of  -thin maps
-thin maps 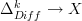 .
.I think you are also right that a plausible guess for the dg-version of it is just
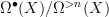 .
.And in fact the infinitesimal simplicial object correspomnding to that should just be the infinitesimal singular simplicial complex
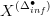 truncated abve degree
truncated abve degree  .
.Yes I think with all this one can decompose the obstruction problem of extending along
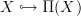 into an infinite sequence of obstruction problems.
into an infinite sequence of obstruction problems.There are actually some examples of this in the literature. For instance some people like to study "abelian gerbes with connection but without curving". What this really means is studying the 2-functors
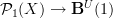 for G a 2-group, instead of
for G a 2-group, instead of 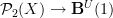 . I have some thoughts on how this is needed for describing the intgeration of Courant algebroids. But it did never really solidify so far.
. I have some thoughts on how this is needed for describing the intgeration of Courant algebroids. But it did never really solidify so far. -
- CommentRowNumber17.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 8th 2010
<div> Urs,<br/><br/>nothing to apologize! one writes things in a forum so that others can read them when they have time. the day I'll want you to immediately reply I'll use Skype instead, I promise :-)<br/><br/>but let us come back to n-connections. I'm glad you like my point of view. I'll try to develop it better as february (and exams..) ends. there's a point in what you write that confuses me:<br/><br/><blockquote><br/>2-functors for G a 2-group<br/></blockquote><br/><br/>do you mean<br/><br/>2-functors for G a 2-group? </div> -
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeFeb 8th 2010
Er, right, I changed what I wanted to say here while saying it. Of course we can look at this for any
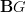 , but what I meant to say is that in the literature, this appears sometimes, but only for
, but what I meant to say is that in the literature, this appears sometimes, but only for 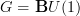 then. At least as far as I have seen. Not that this means anything, I just meant to indicate what of these generally sensible ideas already has a faint indication in existing literature.
then. At least as far as I have seen. Not that this means anything, I just meant to indicate what of these generally sensible ideas already has a faint indication in existing literature. -
- CommentRowNumber19.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
if we keep ourselves to the general defintions how we've been developing them above,the notion of a 2-functor is not entirely correct. namely is now an -category, and we should consider -functors or 2-functors . however, it is possible that in the case the fact that has no higher homotopy implies that the two notions are equivalent. -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
that's true, right. Yes, that's the way it is.
-
- CommentRowNumber21.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 11th 2010
started recollecting and cleaning the material from this thread. page flat infinity-connections created in my nLab area. -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
- (edited Feb 11th 2010)
Thanks, I am reading. It is a delight to see you pick up these observations.
Here is one general remark that should be made at some point:
there is a subtlety hidden here that to the unattentive eye may look like making the whole construction become void, while it is axctually the crucial thing that makes the theory tick here:
namely at the point where you come to the mapping cone of the identity, the informed reader should get worried that you are just describing the point in a sophisticated manner.
Because
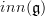 is weakly equivalent to the point. The Weil algebra
is weakly equivalent to the point. The Weil algebra 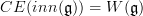 has trivial cohomology. So the mapping space of oo-Lie algebroupoids
has trivial cohomology. So the mapping space of oo-Lie algebroupoids 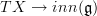 is contractible: every such non-flat connection is gauge equivalent to the trivial one!
is contractible: every such non-flat connection is gauge equivalent to the trivial one!Why is that? Because the gauge transformations of morphisms
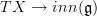 are more than what should be a gauge transformation of a 1-connection. Since this is really now a flat 2-connection, the gauge transformations are those of 2-connections. And these may act by shifting the 1-form part by simply adding a (non-closed) 1-form. But that's of course no longer a gauge transformation of the original 1-form connection.
are more than what should be a gauge transformation of a 1-connection. Since this is really now a flat 2-connection, the gauge transformations are those of 2-connections. And these may act by shifting the 1-form part by simply adding a (non-closed) 1-form. But that's of course no longer a gauge transformation of the original 1-form connection.So what's really happening is that in the contractible space of maps
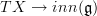 one needs to "carve out" the space of connections and their gauge transformations.
one needs to "carve out" the space of connections and their gauge transformations.This is accomplished by realizing that
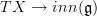 is really one component map in a diagram of such morphisms. You have seen these double square diagrams on my webpage and maybe elsewhere, I suppose. The admissable gauge transformations are those of the entire diagram, and that constrains the transformations of TX --> inn(g) in the correct way.
is really one component map in a diagram of such morphisms. You have seen these double square diagrams on my webpage and maybe elsewhere, I suppose. The admissable gauge transformations are those of the entire diagram, and that constrains the transformations of TX --> inn(g) in the correct way.Told this way, this may look like a big hack hust to fix tings. But quite the opposite is true: one can see that the oo-groupoid of these diagrams naturally occurs as the "curvature-twisted flat differential cohomology" of X. Whatever that means, it means that these diagrams are given from the gods to us and not man-made.
Indeed, one can see that the old notion of Ehresmann connection, at least when formulated in Cartan's style, expressed precisely such a diagram, with three ingredients:
a non-flat 1-form on the total space of the bundle (that's the piece you currently describe on your page)
with a first constraint: restricted to the fibers it has to become flat
and a second constraint: the curvature characteristic classes formed from it have to descend to the base space.
It's these two constraints that also constrain the gauge transformation of
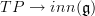 such as to be what we expect them to be.
such as to be what we expect them to be.The abstract nonsense-punchline of all this: non-flat differential cohomology is really twisted cohomology, namely curvature (or chern-character-)twisted flat differential cohomology.
This simple-sounding sentence has a precise formal meaning, and unwinding what this means in detail produces the fact that we want to be looking at morphisms
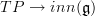 that are constrained to sit in a certain diagram of other oo-Lie algebroid morphisms.
that are constrained to sit in a certain diagram of other oo-Lie algebroid morphisms. -
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
I am not sure if I am following your notation
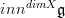 . Could you say this in more detail?
. Could you say this in more detail? -
- CommentRowNumber24.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 11th 2010
meant the iteratd , times. this should have accounted for gaining one "degree of flatness" at each step. but it was wrong: as you remark above, a single step is enough, since is already contractible. now I'm going to correct it. -
- CommentRowNumber25.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 11th 2010
included above remarks into flat infinity-connections. to be continued, but I'll be unable to before a week or so. in the meanwhile feel free to edit/rewrite what I wrote. -
- CommentRowNumber26.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 12th 2010
I'm now thinking everithing I wrote at flat infinity-connections should be rewritten in terms of differential forms on the total bundle of . more precisely the pull-back should be considered, as in L-infinity algebra connections and applications to String- and Chern-Simons n-transport. I'll start editing now, but in at most an hour I'll have to quit. -
- CommentRowNumber27.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 12th 2010
added short paragraph "canonical vertical flat connection" -
- CommentRowNumber28.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 14th 2010
- (edited Feb 14th 2010)
cleaned up the whole entry. final section on gauge and homotopy equivalence of connections still to be written. main point in the cleaning up: "connection" now means "flat oo-connection"; "classical" conections are renamed "preconnections". my feeling is that this makes the whole theory cleaner: what is difficult/odd in the classical theory is so since one pretends to deal with only an approximation of the "real" object.
warning: connection as I'm developing them in the entry do not coincide with Urs' notion of oo-connection which inspired them. my feeling on this is that Urs' notion makes a lot to preserve the classical notion while at the same time exapnding it and including it into an higher perspective (a classical connection is an Urs' connection), while the simpler definition I'm pursuing is more drastic with respect to the classical one (a classical connection is not a connection as I'm defining it, but only a partial datum of a connection). I'd be extremely interested in seeing how the examples which motivated Urs' definition fit with the notion I'm thinking to. -
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeFeb 15th 2010
- (edited Feb 15th 2010)
Is what you write really different from what I was talking about, or not more a refinement of the situation, in that you discuss the cotower in between
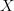 and
and 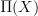 ?
?By the way, I thought about the push-forward and quantization of differential cocycles: at least the kind of connections that I am talking about are objects in the homotopy fiber of a Chern-character map
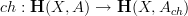 . If the codomain and domain object here have push-forwards, then this induces a push-forward on the homotopy fiber. I think this is the right notion of push-forward and quantizaiton of differential cohomology.
. If the codomain and domain object here have push-forwards, then this induces a push-forward on the homotopy fiber. I think this is the right notion of push-forward and quantizaiton of differential cohomology.Notably when A is fully abelian, I think this reproduces the standard notion of push-forward in ordinary "abelian" differential cohomology.
I think. But I haven't written this out in full detail yet.
-
- CommentRowNumber30.
- CommentAuthordomenico_fiorenza
- CommentTimeFeb 15th 2010
- (edited Feb 15th 2010)
no, it shouldn't be different (at least in my intentions). and the intermediate cotower in between and I'm now looking at as somethig not so important: what really counts are only and . the main difference between your point of view and mine, seems to be that I'm stressing attention of flat connections, willing to forget any structure that is not an oo-flat connection. in your approach (as far as I understand it) the classical datum is conserved, so that a connection is a classical datum which sits into a larger picture. this is surely useful when one is faced with existing literature, but I'm wondering whether starting from zero one would arrive to such a subtle notion, rather than directly considering oo-flat connections.
I mean: if my only categorical tool are groupoids, as in a sense it has been for several years, then the only groupoids I can see in are and . and since I'm naturally used to consider linear representations of "group-like things", I'm naturally led to functors and , that is, connections and flat connections. ok, this is classical, nothing to say about.
but assume things had gone differently, one had not the habit of quotienting out equivalences, but to keep them. in other words, the groupoid one would have naturally seen in is . then one would have directly considered representations . or (since it is not clear to em what oo-Vect should precisely be) representations , with an oo-group.
also one would have the inclusion inducing , which could be a nice candidate for the refinement from cohomology to differential cohomology.
so my question in the last post was: what happens of Kalb-Ramond, RR, C-fields.. if one just forgets about the classical theory and restarts from zero? can we say something like: take this oo-group and this representation of , and that's it? -
- CommentRowNumber31.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 3rd 2010
back to work :)
I still have to recollect myself, so today's post will be a bit vague and confused, I apologize for that.
is a Lie algebra, is a Lie group integrating it, then a valued connection on a trivial principal -bundle on a manifold is a 1-form on with values in , i.e. a degree 1 element in the dgla , where is the de Rham algebra of . integrating gives a functor . this can be seen as an oo-functor from the nerve of to the nerve of . it is a remarkable result by Hinich that this latter nerve is homotopy equivalent to the Kan complex , where denotes the set of solutions of the Maurer-Cartan equation in a dgla. using this model for , the functor is straightforwardly described: a path is mapped to the degree 1 element in . This element is automatically a Maurer-Cartan element, since is a 2-form and so it vanishes when pulled back via . by the very same reason, is a Maurer-Cartan element in for every thin map (by definition of thin map). hence we have the seeked functor.
Trying to lift to a functor stemming from we meet the curvature obstruction: for a generic map , the element is not a Maurer-Cartan element in unless is flat. once we require to be flat, we are done: what we are asking is that is a Maurer-Cartan element in , and so it will produce Maurer-Cartan elements wherever we pull it back. in particular the functor can be lifted to for any , and so to a functor from .
this is very much a 0-1 situation: either we are blocked on or we have vanishing curvature. to cook something intersting with nontrivial curvature, let us move from Lie algebras to -Lie algebras, which will be convenient to think as -algebras concentrated in degrees . Getzler shows in his work on Lie theory for nilpotent algebras, that the Maurer-Cartan construction sketched above verbatim generalizes from Lie algebras to -Lie algebras (it is possible some version of this result predates Getzler, it seems I'm quite unable to give proper credits for results..). so let us take for instance a 2-Lie algebra , where is the subspace of degree elements. since the higher brackets have degree , for a 2-Lie algebra only the following brackets survive:
now, consider a manifold and the -algebra (it is an -algebra concentrated in degrees ). a flat connection on a trivial principal -bundle on (where is the 2-group integrating ) is a solution of the Maurer-Cartan equation
on . the 2-bracket and the 3-barcket come from the 2- and 3-bracket in ; the differential has a contribution from the 1-bracket of and one from the de Rham differential .
(to be continued...) -
- CommentRowNumber32.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 4th 2010
- (edited Mar 4th 2010)
a particularly simple and interesting case is when is the Lie 2-algebra , i.e., the Lie 2-algebra coming from the crossed module , for a Lie algebra in this case, , , the 3-bracket vanishes, the 2-brackets are just the 2-brackets of , and the differential is the identity of . A flat -connection on has the form , with a 1-form on with coefficients in , and a 2-form on with coefficients in (and so with some abuse we can think of as a 2-form with coefficients in ; we should avoid doing so, since degrees are relevant, but let us note this in order to make contact with a familiar picture..).
Then the Maurer-Cartan equation for has the form
the -degree makes a set of several equations out of the single equation above (one for each degree). using the explicit expressions for the brackets we see that we actually end up with just two equations, one for a 2-form, and one for a 3-form. namely,
and
where have I already seen these equations? :)
(enough for today.. in next post we'll see how a Chern-Simons term appears as soon as we allow a nontrivial 3-bracket) -
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeMar 4th 2010
Hi Domenico.
Thanks. After I get a bunch of other things out of the way, I get back to you here. Meanwhile, the standard question: wouldn't that better be typed into a page? :-)
-
- CommentRowNumber34.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 5th 2010
Hi Urs.
here's the standard answer: I've now copied the last two post of mine here in a "Maurer-Cartan equations" section in flat infinity-connections, and added a discussion box at the end of it :-) -
- CommentRowNumber35.
- CommentAuthorzskoda
- CommentTimeJul 21st 2010
There are so many entries in nlab on connections so I do not know which ones are the most appropriate for (a link to) nice Beilinson-Kazhdan manuscript on geometric quantization using connection in relative context:
- A. Beilinson, D. Kazhdan, Flat projective connections, http://www.math.sunysb.edu/~kirillov/manuscripts/kazhdan2.pdf
Here the basic object is p-connection: for a smooth morphism p of smooth analytic spaces or of smooth schemes p:X→S they define a p-connection as 𝒪X-linear map ∇S:p*TS→TX such that dp∘∇S=idp*TS. The “differential” dp here is I guess in fact the map TS→p*TX induced by the universality of the pullback and the differential. p-connection is flat/integrable if the corresponding (by adjunction) map TS→p*TX commutes with brackets of vector fields.
-
- CommentRowNumber36.
- CommentAuthorzskoda
- CommentTimeJul 29th 2010
I have entered the above remark as a new entry p-connection (maybe a better title is deserved; my guess is that one should take the resolution of the diagonal of the map p, which gives the corresponding infinitesimal neighborhood (roughly like the neighborhood of the diagonal in the Čech resolution) and look for more “ordinary” connections there.
1 to 36 of 36