Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: structures in a gros (oo,1)-topos

Bottom of Page

1 to 4 of 4

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeFeb 9th 2010
    • (edited Feb 9th 2010)

    I thought I'd amuse myself with creating a succinct list of all the useful structures that we have canonically in an (oo,1)-topos without any intervention by hand:

    • principal oo-bundles, covering oo-bundles, oo-vector-bundles, fundamental groupoid, flat cohomology, deRham cohomology, Chern character, differential cohomology.

    I started typing that at structures in a gros (oo,1)-topos on my personal web.

    I think this gives a quite remarkable story of pure abstract nonsense. None of this is created "by man" in a way. It all just exists.

    Certainly my list needs lots of improvements. But I am too tired now. I thought I'd share this anyway now. Comments are welcome.

    Main point missing in the list currently is the free loop space object, Hochschild cohomology and Domenico's proposal to define the Chern character along that route. I am still puzzled by how exactly the derived loop space should interact with 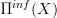\Pi^{inf}(X) and \Pi(X).

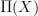    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010

    expanded my collection of canonical structurs in an (oo1,)-topos a bit further

    structures in a gros (oo,1)-topos

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010

    have been further expanding and streamlining formal structures in an (oo,1)-topos.

    Find it quite pleasing what a whealth of structures comes out for free here.

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeFeb 19th 2010
    • (edited Feb 19th 2010)

    one more:

    I think an object X in an (oo,1)-topos is

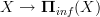    • formally smooth if X \to \mathbf{\Pi}_{inf}(X) is an effective epimorphism .

    With the notation as in the entry.

    This is supposed to be the derived and generralized version of what Simpson-teleman have on p . 7

1 to 4 of 4

  1.