nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
I thought I'd amuse myself with creating a succinct list of all the useful structures that we have canonically in an (oo,1)-topos without any intervention by hand:
- principal oo-bundles, covering oo-bundles, oo-vector-bundles, fundamental groupoid, flat cohomology, deRham cohomology, Chern character, differential cohomology.
I started typing that at structures in a gros (oo,1)-topos on my personal web.
I think this gives a quite remarkable story of pure abstract nonsense. None of this is created "by man" in a way. It all just exists.
Certainly my list needs lots of improvements. But I am too tired now. I thought I'd share this anyway now. Comments are welcome.
Main point missing in the list currently is the free loop space object, Hochschild cohomology and Domenico's proposal to define the Chern character along that route. I am still puzzled by how exactly the derived loop space should interact with
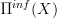 and
and 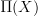 .
. -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 19th 2010
expanded my collection of canonical structurs in an (oo1,)-topos a bit further
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 19th 2010
have been further expanding and streamlining formal structures in an (oo,1)-topos.
Find it quite pleasing what a whealth of structures comes out for free here.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 19th 2010
- (edited Feb 19th 2010)
1 to 4 of 4
 in an (oo,1)-topos is
in an (oo,1)-topos is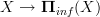 is an effective epimorphism .
is an effective epimorphism .