Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: axioms of choice

Bottom of Page

1 to 45 of 45

  1.  
    • CommentRowNumber1.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 10th 2010

    I wrote a bit about the axiom of multiple choice and about SOSHWIS (a terrible name, but I didn't have time to think of anything better), with comments at axiom of choice and anafunctor and COSHEP.

    • CommentRowNumber2.
    • CommentAuthorAndrew Stacey
    • CommentTimeFeb 10th 2010

    Good thing you logged this! I just looked at the RSS feed for the nLab and though "A-ha! The spammers are back. SOSHWIS is clearly some fancy acronym for essay writing."

    • CommentRowNumber3.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)
    "The name 'SOSHWIS' is a word that I coined myself, spending a week thinking of nothing else."
    • CommentRowNumber4.
    • CommentAuthorTodd_Trimble
    • CommentTimeFeb 10th 2010

    I hope SOSHWIS makes it into the Official Scrabble Player's Dictionary one day.

    • CommentRowNumber5.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 10th 2010
    • (edited Feb 10th 2010)
    Is 'operad' in said dictionary?
    • CommentRowNumber6.
    • CommentAuthorTodd_Trimble
    • CommentTimeFeb 10th 2010

    Harry, no it ain't, nor are scads of other plausible-looking math terms. The OSPD is a very odd compilation with no real scholarly authority; its only real purpose is to provide an official backbone for the board game.

    I was joking, of course. But it would be a nice "bingo" (7-letter) word using the unpleasant combination HIOSSSW!

    • CommentRowNumber7.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 10th 2010
    So is it Sos - hwiz or Sosh-wiz?
    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010

    That made me laugh out loud. Thanks. :-)

    • CommentRowNumber9.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 10th 2010
    I do hope that everyone here gets the joke :

    "The name '______' is a word that I coined myself, spending a week thinking of nothing else."

    I assume Mike gets it because he's at Chicago.
    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010

    I do hope that everyone here gets the joke :

    Sure.

    • CommentRowNumber11.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 10th 2010
    That makes me very happy.
    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeFeb 10th 2010

    It's certainly a great strategic move to make the sentence "I coined this concept and term." a good joke that everyone likes to remember. There are less promising strategies, as for instance the plead hidden here. ;-)

    • CommentRowNumber13.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 10th 2010

    @Harry, that's the second or third time you've tried to make that "joke." Of course I "get it," but I've been ignoring it in hopes of discouraging you from continuing to make it. (-: Evidently a poor strategy.

    • CommentRowNumber14.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 10th 2010
    But Mike, that is a great joke! I learned it from Mitya Boyarchenko.
    • CommentRowNumber15.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 11th 2010

    As an internal category theorist (if there is such a thing) I itch to state this for categories other than Set. Or rather, other sites 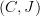(C,J). For concrete categories this should be obvious, but more generally this will be a fantastic addition to the survey article on internal anafunctors I will write after my thesis is examined. (you may know it as the good ol' chapter 1).

    One of my internal arguments (to convince myself) for anafunctors as a presentation for the localisation of the 2-category of internal groupoids/categories is that the hom-categories are essentially small (at least in Top, and with AC in Set as implicit)- clearly an axiom such as this is necessary. Thank you Mike!

    • CommentRowNumber16.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 11th 2010
    • (edited Feb 11th 2010)

    Added the stuff about an internal version to SOSHWIS, but of course it needs a proper name for it to be applicable. How about:

    WISC: weakly initial set of covers

    CSC: cofinal set of covers

    with preference to the latter, for my part

    • CommentRowNumber17.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 11th 2010

    I would prefer WISC, myself. I think "cofinal" is a bit confusing, because firstly "cofinal" has also been used to mean the same as "final" when applied to a functor, and secondly a weakly initial set isn't, as far as I can tell, "cofinal" in the dual sense to "final functor".

    • CommentRowNumber18.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 11th 2010

    Sure. I tend to think in analogy with cofinal covers, and 'weakly initial' to my mind doesn't seem to tie so closely to the case of a non-singleton pretopology, but then, the main application (viz. anafunctors) requires a singleton pretopology anyway. And technically speaking weakly initial is entirely accurate as to describing cofinal non-singleton pretopologies, given the right definition of category of covers of an object.

    WISC also has the benefit of being a single syllable. It now has my vote if such a thing is necessary.

    • CommentRowNumber19.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 11th 2010
    Mike, why is it that a lot of your foundations-related terms are capitalized acronyms?
    • CommentRowNumber20.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 11th 2010

    where "a lot" = 2? I suppose in higher category theory, n=2 is getting close to "a lot".

    • CommentRowNumber21.
    • CommentAuthorDavidRoberts
    • CommentTimeFeb 12th 2010
    Added proposal of WISC to SOSHWIS and result about internal anafunctors in other sites.
    • CommentRowNumber22.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 12th 2010

    I renamed the page and all its references. We can still keep looking for a better name if we want, but I think WISC is indisputably better than SOSHWIS, so there's no reason not to use it preferentially for now.

    I also added some more detail explaining why Top satisfies WISC (if Set satisfies AC). It would be interesting to write out the modifications necessary if Set only satisfies WISC itself, but I don't have time to figure those out right now.

    • CommentRowNumber23.
    • CommentAuthorHarry Gindi
    • CommentTimeFeb 12th 2010

    Didn't you invent COSHEP and SEAR?

    • CommentRowNumber24.
    • CommentAuthorMike Shulman
    • CommentTimeFeb 12th 2010

    No, COSHEP is not my fault. I think Toby invented that; everyone else I've seen abbreviates it as "PAx" (for "presentation axiom") or "EPSets" (for "enough projective sets").

    • CommentRowNumber25.
    • CommentAuthorUrs
    • CommentTimeMar 12th 2012
    • (edited Mar 12th 2012)

    Since elsewhere Mike is now calling the definition currently stated at axiom of choice “naive”, I briefly added a sentence on In dependent type theory.

    Hopefully eventually we expand on this (the whole entry might do with a bit more restructuring), for the moment I just leave it there as a reminder.

    • CommentRowNumber26.
    • CommentAuthorMike Shulman
    • CommentTimeMar 12th 2012

    My use of “naive” elsewhere was in reference to higher categories, but I suppose that if one identifies the internal logic of (∞,1)(\infty,1)-categories with HoTT then that could be considered similar to DTT. (-:

    • CommentRowNumber27.
    • CommentAuthorUrs
    • CommentTimeMar 12th 2012

    That’s what I was thinking: the way that the axiom of choice does hold in GrpdGrpd is the way that it does hold in dependent type theory, isn’t it?

    • CommentRowNumber28.
    • CommentAuthorMike Shulman
    • CommentTimeMar 13th 2012

    Are you thinking of the fact that “AC” is provable in the propositions as types logic? I would have said rather that the sense in which AC holds in Gpd (at least, a Gpd based on a classical Set) is more like this.

    • CommentRowNumber29.
    • CommentAuthorTobyBartels
    • CommentTimeMar 13th 2012

    Urs, your phrasing ‘in the internal logic’ is not correct; the definition there is the external axiom of choice; putting AC in the internal logic gives a different statement, the internal axiom of choice (which ought to be discussed on the page as well). There is some stuff about this in MacLane & Moerdijk; I don’t have that with me, but one should be able to find it in the index under ‘internal axiom of choice’ or maybe ‘IAC’.

    • CommentRowNumber30.
    • CommentAuthorMike Shulman
    • CommentTimeMar 13th 2012

    I thought that by “the axiom of choice says that in the internal logic of a given ambient category the following statement holds” Urs meant that “the axiom of choice” refers to the internal version, as that can be obtained by internalization of the statement “every epimorphism splits”. But regardless of the original intent, it could all certainly be more clear. I added a mention of this in a subsection “Variations”.

    • CommentRowNumber31.
    • CommentAuthorTobyBartels
    • CommentTimeMar 13th 2012

    Perhaps he did mean that, but then that begs the question of what that means; it’s not so obvious how to internalise that statement in most categories.

    I would distinguish between whether the axiom of choice holds in a category, which is the internal version, and whether it holds of a category, which is the external version.

    • CommentRowNumber32.
    • CommentAuthorMike Shulman
    • CommentTimeMar 13th 2012

    It’s easy to internalize in the stack semantics. For that, you just need a pullback-stable notion of “epimorphism”.

    I can see your idea with the language, but I’m not sure it’s worth training myself to consistently assign those meanings to those prepositions. (-:

    • CommentRowNumber33.
    • CommentAuthorUrs
    • CommentTimeMar 13th 2012

    I wasn’t being nearly as sophisticated as you are now when I quickly typed those words. I was promted by finding that the entry didn’t explain enough to the average reader in the first sentences why on earth it states the axiom of choice in a way very different from how ordinary people state it (meaning: non-category theorists).

    I remember vividly some years ago over dinner after a conference, at a table full of professional mathematicians, the discussion happened upon the axiom of choice, and when I claimed that it is to be interpeted simply as saying that in the ambient category all epimorphisms split, the general feeling was that this was the most outlandish thing that people had heard.

    So please feel free to improve to your heart’s content. But let’s eventually try to start the Idea-section with something that leads in more gently.

    • CommentRowNumber34.
    • CommentAuthorTom Leinster
    • CommentTimeMar 13th 2012

    Urs:

    when I claimed that it is to be interpeted simply as saying that in the ambient category all epimorphisms split, the general feeling was that this was the most outlandish thing that people had heard.

    It’s extraordinary, isn’t it?

    Conversely, I just had a student doing a project on categorical set theory. Part-way through, she came to see me and said she’d been hearing a lot of mysterious stuff about the axiom of choice and wanted to know what it was. I told her “every surjection has a section” and she had an amazed reaction of “is that all?”; she coudn’t believe there was so much fuss about it. I guess she understood a bit better when she started finding out about Banach-Tarski etc. But still, I felt happy that her first encounter with it was this very simple, concrete, direct formulation.

    • CommentRowNumber35.
    • CommentAuthorTodd_Trimble
    • CommentTimeMar 13th 2012

    I remember when I told a fellow graduate student about this way of formulating AC, and his reaction was to stare off in space and then almost immediately say, “That’s right!” There was a kind of delight in his tone, and it encouraged me to say more.

    He was an analyst, if I recall correctly, and I think he may have had geometric tendencies. It’s really a geometric formulation in a way: you picture this bundle you want a section of. It ought to appeal greatly to an algebraic topologist.

    Too bad, Urs, you got that reaction – it’s not as if you defined a topological space to be a relational β\beta-module!

    • CommentRowNumber36.
    • CommentAuthorTobyBartels
    • CommentTimeMar 13th 2012

    it’s not as if you defined a topological space to be a relational β\beta-module

    a definition which is only correct assuming the axiom of choice (well, the ultrafilter principle)

    • CommentRowNumber37.
    • CommentAuthorTodd_Trimble
    • CommentTimeMar 13th 2012

    That’s quite true, Toby, but slightly orthogonal to the sociological point I was making. :-)

    • CommentRowNumber38.
    • CommentAuthorTobyBartels
    • CommentTimeMar 14th 2012

    Indeed, I just appreciated the irony (well, not exactly irony).

    • CommentRowNumber39.
    • CommentAuthorMike Shulman
    • CommentTimeAug 18th 2013

    I added some more detail at axiom of choice about higher-categorical versions and homotopy type theory.

    • CommentRowNumber40.
    • CommentAuthorBrian Pinsky
    • CommentTimeJan 3rd 2021

    There is a classical set theory axiom also called “the axiom of multiple choice”, and it appears to be unrelated to axiom with that name on the nlab.

    The set theory axiom is described in jech’s book “the axiom of choice” (chapter 9), as well as some other places in the literature. The axiom says this: If SS is a set of non-empty sets, there is a function ff defined on SS such that for all X∈SX\in S, f(X)f(X) is a non-empty, finite subset of XX.

    This does not appear equivalent to any of the definitions in axiom of multiple choice (although I am struggling to make a concrete proof of this fact). The axioms are historically unrelated, and it is rather unfortunate that the have the same name.

    Unfortunately, it seems it’s a bit too late to change the name of either axiom, but I’d like a way of unambiguously referring to them. I’m thinking of saying “categorical axiom of multiple choice” for the nlab axiom, and replacing it wherever it occurs (as, intuitively, the name “axiom of multiple choice” seems like a much closer description of the set theory axiom). I’m open to other naming ideas but I’d like some input from the people who named this axiom in the first place so I don’t offend anyone.

    In the mean time, I’m going to edit the nlab page to also mention this older axiom and include some references for it. I can also describe some interesting properties of this axiom (it’s actually equivalent to full AC modulo classical ZF set theory; but it is strictly weaker under ZFA. I don’t know a super neat proof as fundamentally it works by induction on rank). It would seem appropriate to include some nice catigorification of the statement as well, but I don’t know of one that isn’t just translating this into a topos’s internal logic. If you’re trying to think of one, another equivalent statement that might be helpful is: “every set has a surjection onto an ordinal such that every fiber is finite” (I think choice object is the appropriate generalization of ordinal here for arbitrary categories) (it’s easy to prove the equivalence; just mimic the proof of the well ordering theorem from AC)

    I’d also like to add clarifying wording to other pages that mention this axiom, so it’s clear which axiom they mean, but I’d like some agreement about names for these axioms first.

    • CommentRowNumber41.
    • CommentAuthorTodd_Trimble
    • CommentTimeJan 3rd 2021
    • (edited Jan 3rd 2021)

    This is only a suggestion, but the page axiom of multiple choice refers to an axiom in constructive mathematics where the law of excluded middle is not assumed. Whereas I think the notion you’re referring to appears in texts where the LEM is tacitly assumed. So one possibility is to include a disambiguating paragraph at axiom of multiple choice saying this page is about the an axiom in constructive mathematics, and add something like this: “In other texts, the term ’axiom of multiple choice’ may be used to refer to a certain weakened form of the axiom of choice in the context of classical (non-constructive) set theory. For that notion, [see here](classical axiom of multiple choice).” (Create a page that gives this other notion.)

    It’s likely that references within the nLab are going to point to the constructive version, so you wouldn’t really have to add clarifying wording to other pages that point to it. The reader can find out with a single click. If a need at some later page is felt to point to the classical set theory notion, then hyperlink to (classical) axiom of multiple choice.

    • CommentRowNumber42.
    • CommentAuthorBrian Pinsky
    • CommentTimeJan 3rd 2021
    I like Todd's suggestion; you're right that all the sources assume LEM without a second thought, and it avoids me having to hunt down every place where AMC is referenced.

    Also, I believe I have a proof that the classical axiom of multiple is not equivalent. The model where multiple choice holds but choice fails is a permutation model, hence it should satisfy small violations of choice. SVC proves the categorical AMC, which means this model should satisfy one and not the other.

    I'll implement your suggestion when I'm done reading a few of the SVC papers so I can be more confident that my proof works.
    • CommentRowNumber43.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 3rd 2021

    Thanks, Brian, for looking into this.

    The AMC due to van den Berg is usually called WISC here on the nLab, and even in papers by various authors. Aside from this, his version was set up to work in predicative foundations, not just in the absence of LEM.

    Going back to the traditional AMC, can it not be stated as a section S→∐ X∈SP fin,ne(X)S\to \coprod_{X\in S} P_{fin,ne}(X)? The latter is the fibrewise finite, nonempty power set, where we think of SS as the codomain of a surjective function pp, and it is equipped with a canonical map to SS. I then want to say this should give a finite-to-one surjective map T→ST\to S and a section of pp over TT.

    • CommentRowNumber44.
    • CommentAuthorBrian Pinsky
    • CommentTimeJan 4th 2021

    David’s formulation is correct I believe, but I’m not sure it adds generality. Interpreting such a statement in a topos requires choosing an appropriate notion of finite and an appropriate notion of ⨿ X∈S\amalg_{X\in S}. I’m also not strictly sure what non-empty would mean (I don’t know if “has a global element” is too strong).

    Another related classical axiom that perhaps deserves some discussion is the axiom of choice from finite sets, which says that any set of finite sets has a choice function (or, as my friend likes to put it, finite covers of discreet spaces have sections). This is independent from multiple choice, and clearly the two together imply full choice. Both axioms orthogonal to things like countable choice, which is better known among most mathematicians

    • CommentRowNumber45.
    • CommentAuthorDavidRoberts
    • CommentTimeJan 4th 2021

    Non-empty/coproduct is not a problem. What one wants, if it is correct, is this:

    For every epi p:X→Sp\colon X\to S, an epimorphism q:T→Sq\colon T\to S that in the topos E/SE/S is a finite object (for a given notion of finite) and the map s:T→Xs\colon T\to X, with q=p∘sq = p\circ s.

    There will be one such axiom per definition of “finite” in a topos (see: finite set).

1 to 45 of 45

  1.