nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
added to homotopy coherent nerve two diagrams in the section Examples and illustrations that are supposed to illustrate the hom-SSets of the simplicial category on
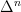
-
- CommentRowNumber2.
- CommentAuthorTim_Porter
- CommentTimeFeb 11th 2010
I have added several 'old' references to this. As one of the originators of that theory I get a bit 'browned off' by papers that do not make any mention of Vogt, Cordier (and of course myself). As I feel a bit like moaning, I would say that some of the papers I have seen show a lack of 'scholarship' in this regard. (end of moan.. promise!)
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
I think it is good that you make these points! I am certainly interested in getting this information from you.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
I have now made some more of the author names link to their respectivbe nLab entries: Boardman, Vogt and you. Maybe you could create a page for Cordier?
-
- CommentRowNumber5.
- CommentAuthorTim_Porter
- CommentTimeFeb 12th 2010
WIll do (in time!)
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeJan 17th 2011
- (edited Jan 17th 2011)
I added the following text in homotopy coherent nerve (I hope correct; I learned this roughly from Joyal’s texts, but blame me if I misinterpreted) and reorganized the definition part:
Recall that a reflexive graph is a simplicial set of dimension 1, i.e. 1-coskeletal; they form a full subcategory reflGraph↪Cat. The forgetful functor U:Cat→reflGraph has a left adjoint F hence G=FU:Cat→Cat is a comonad. By the definition its cobar construction is an augmented simplicial endofunctor S→Id featuring S:Δ→sSetCat and whose augmentation is a cofibrant replacement of a 1-category in the Bergner model structure on sSetCat (“model structure for simplicially enriched categories”).
(By the way if David Roberts is around, he wondered about usual nerves on the history of the distinction between looking it as simplicial sety and as a topological space – of course for simplicial complexes the passage back and forth was elementarily well known since 1920s (about the same time when Aleksandrov introduced a nerve of a covering) but the full fledged treatment and the definition of a geometric realization is due John Milnor: The geometric realization of a semi-simplicial complex. Ann. of Math. (2) 65 (1957), 357–362 (of course at the time simplicial sets were “complete semi-simplicial complexes”). This is about the same time as Grothendieck started looking at more general nerves of categories.)
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeJan 17th 2011
Here I archive two discussions from query boxes at homotopy coherent nerve
QUERY 1
Todd: I am learning this for the first time, and I had some difficulty with how the definition of Pi,j reads. From the ensuing discussion, it seems you want the elements of the poset to be I⊆[i,j]:i,j∈I, ordered by inclusion. But in the definition, it’s not clear what sort of thing J is supposed to be, and it looks like the elements of the poset are instances of inclusions. (Another minor thing I don’t understand is why ⊂ is being used instead of ⊆, since for many mathematicians ⊂ means strict inclusion. I see this preference for ⊂ all over the nLab in fact; has this been discussed somewhere?)
Tim: I did not originate the poset based description as I always think of things as being paths through the N-simplex from i to j and then use a rewrite idea for the link. I will try to clean up the poset definition a bit and see if it helps, otherwise we can switch to the path based description and use the poset as a second way. I’m not bothered either way.
Some minutes later! Does this read well now?
Todd: Thank you! Yes, me happy now.
QUERY 2 – on terminology (at the time, it was at the entry then called simplicial nerve of simplicial categories)
Is there a simplicial nerve that's not of simplicial categories? If not, I'd put the article here instead of there. —Toby
Urs: yes, it seems to be called just “simplicial nerve” in the literature, but I found that a bit undescriptive, since every nerve is “simplicial” and here the point is really that we take the nerve of a simplicial category. I also seem to recall that Tim said he doesn’t like the term “simplicial nerve”. Maybe Tim should decide, he is probably the one among us who has thought about this notion the most.
Toby: Ah, I see how ’simplicial nerve’ is confusing; so how about just nerve of a simplicial category?
Urs: right, that might be the best option – I have to run now, maybe you can implement that?
Toby: I'll wait to hear from Tim.
Mike: Not all nerves are simplicial; it depends on what you are taking the nerve of. The nerve of a multicategory is a dendroidal set (a presheaf on the category of trees). The nerve of a compact symmetric multicategory is a presheaf on the category of Feynman graphs. And an n-category has a nerve that is a simplicial set, but also one that is a Θn-set and one that is an n-fold simplicial set.
FWIW, I have sometimes seen the “simplicial nerve of simplicial categories” called the “homotopy coherent nerve,” which to me captures the intuition better.
Urs: true, I actually know that not every notion of nerve is simplicial, should have thought before typing.
Now that you mention it, maybe Tim Porter also said he favored “homotopy coherent nerve”? I’ll send him an email.
Tim: Back from a short absence: the term ’homotopy coherent nerve’ is probably a good one only when it fairly directly relates to homotopy coherence.
Any 2-category can be thought of as a simplicially enriched category and the Duskin nerve of a bicategory specialises to the same construction on 2-categories. Various people use the term ’geometric nerve’ for this. (It is interesting to compare the ’simplicial nerve’ of a simplicial group (as SSet-enriched category) with Wbar of the same thing.) I am trying to write something for the Menagerie that looks at the h.c. nerve with these aspects accentuated and also with links with Behrang Noohi’s weak maps of crossed modules. I may put some of this on nLab when I see more clearly how it all fits together.
In the meantime, I suggest we keep the term h.c. nerve although it is probably not ’best possible’. I agree that ’simplicial nerve’ is probably not a good term.
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeJan 17th 2011
Hi Zoran, thanks for the pointer to the history. I was thinking more along the lines of how some people these days say ’simplicial space’ and mean bisimplicial set, and when talking about spaces actually mean simplicial set. But once Milnor pointed out the link between sSet and Top, and Kan (I think) showed that sSet modelled all homotopy types, then I suppose those in the know would have been comfortable with switching back and forth. But as you say, simplicial sets came from simplicial complexes, which were definitely used interchangeably with (nice) spaces.
-
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeJan 18th 2011
they form a full subcategory reflGraph↪Cat
Do you mean reflGraph↪sSet?
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeJan 18th 2011
Yes, that is what I meant, but I was writing and erasing various things and somehow the final version got incorrect.
-
- CommentRowNumber11.
- CommentAuthornLab edit announcer
- CommentTimeApr 5th 2018
-
- CommentRowNumber12.
- CommentAuthorTim_Porter
- CommentTimeOct 25th 2018
-
- CommentRowNumber13.
- CommentAuthorGuest
- CommentTimeMay 14th 2021
Hi! The simplicial composition in the object that gives the shape to the homotopy coherent nerve - that is, the object S[n] - is never specified explicitly. It is “fairly obvious”, but indeed there are 2 fairly obvious ways of composing paths: one can keep the intermediate vertex or can discard it. I think these two ways should be somehow canonically isomorphic, but since there is a direction involved 0→1 I am not sure if a “reflection” will do the trick. I would be grateful if someone could come in and fill in this tiny detail! By the subset representation of a path, at the moment I am more convinced of the “discarding” option :)
-
- CommentRowNumber14.
- CommentAuthorGuest
- CommentTimeMay 14th 2021
Hi, still Andrea talking here. There is another tiny detail missing: the object S[n] is cosimplicial in n, but the cosimplicial maps are not specified. A similar problem as before arises: for example, the map d1:[1]→[2] should induce a map S[1]→S[2] that is fixed on objects and makes a choice a∈MapS[2](0,2). The latter can be the path 0→1→2 or 0→2. In general one must choose if plugging in the intermediate vertex, and I suspect we must keep it. In other words, there are two “obvious choices” of the kind “keep or discard”, and I guess they must be opposite.
-
- CommentRowNumber15.
- CommentAuthorTim_Porter
- CommentTimeJul 5th 2021
-
- CommentRowNumber16.
- CommentAuthorHurkyl
- CommentTimeJul 5th 2021
- (edited Jul 5th 2021)
Paths are arrows in the free category of a graph, so composing a path 0→1 with a path 1→2 gives the path 0→1→2. In fact, the underlying 1-category of S[n] is the free category generated by the nondegenerate arrows of [n]. The representation as a subset given in the article intends to be the set of vertices visited, so 12∘01=012. But you could choose alternative representations, such as “the set of endpoints together with the set of intermediate vertices not visited” which, I think, gives the “take the union but drop the intermediate vertex” scheme you were interested in.
The intended action of an order morphism f:[m]→[n] on paths is that Sf applies f pointwise. IIRC, for any simplicial set K, the underlying 1-category of SK is the free category generated by the nondegenerate 1-simplices of K.
-
- CommentRowNumber17.
- CommentAuthorHurkyl
- CommentTimeNov 5th 2021
- (edited Nov 5th 2021)
What are the thoughts on reversing the ordering convention for the hom-spaces?
As written, the nondegenerate 1-simplex of SΔ2(0,2) has the orientation [20]→[21]⋅[10], so it’s depicted more like an oplax operation, which breaks the convention that things are typically formulated in the lax version.
For example, the Duskin nerve page on nLab takes the opposite convention. Lurie also switches over to the opposite convention when he wrote the Kerodon, in notation 2.4.3.1 (simplicial path categories).
If nobody objects I’ll go ahead and make the change.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeNov 5th 2021
Sounds good, please do.
-
- CommentRowNumber19.
- CommentAuthorHurkyl
- CommentTimeNov 5th 2021
-
- CommentRowNumber20.
- CommentAuthorHurkyl
- CommentTimeNov 5th 2021
-
- CommentRowNumber21.
- CommentAuthorHurkyl
- CommentTimeNov 5th 2021
-
- CommentRowNumber22.
- CommentAuthorHurkyl
- CommentTimeNov 5th 2021
-
- CommentRowNumber23.
- CommentAuthorTim_Porter
- CommentTimeNov 5th 2021
Please don’t!!!! There are consequences to changing those conventions so it is better to add a note about the convention rather than changing it. (I know as one of the original developers of the theory, adding a note is not sufficient and shoud not be done unless you are 100% certain that there are no consequences, i.e. that all the parts match!) The two theories are completely equivalent as is clear. In other words I do object.
-
- CommentRowNumber24.
- CommentAuthorHurkyl
- CommentTimeNov 5th 2021
- (edited Nov 5th 2021)
Okay. I’ve tossed out most of my reasons for bringing it up; I should also add that Kerodon uses the changed version (hom-objects are reverse inclusion of subsets) when developing the theory of (∞,2)-categories. E.g. 5.3.7.6 (tag 01YA) of the Kerodon suggesting we view maps Nhc(C)→Nhc(D) as the right generalization of lax functor. (maybe 4.6.6.9 and 4.6.6.10, 01lg and 01lh, can weight in too)
I’ll let people more familiar with the breadth of the theory decide on how to proceed.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeNov 5th 2021
This has nothing to do with the theory, it’s a choice of notation for making a nicely readable entry, and it’s great that somebody is looking into it.
Tim, if you feel attached to this entry, there is much room for you to work on improving it, too. For instance you could turn the array diagrams into
tikzcds. -
- CommentRowNumber26.
- CommentAuthorTim_Porter
- CommentTimeNov 5th 2021
- (edited Nov 5th 2021)
The one main point is that the original definition and the reversed definition result from opposite convention for the simplicial resolution given by an adjoint pair. This has consequences (not serious ones) as to the conventions for the face and degeneracy maps. It would be as well if the same convention was used as in any n-Lab entry on simplicial resolutions, bar constructions etc, and that need a bit of ferreting. I will have a look at the entry to see how it can be tweeked / improved. My objection is not a theoretic one but merely a pragmatic one that adjusting the convention in one part of the entry implies that the rest of the entry has to be checked to see that it is consistent. (I need to look at the entry as I said and it may be that it is safe to do the change without loads of adjustment. I am also fond of the original version as I worked on that with Jean-Marc Cordier but the main reason for my objection was that to check consistency might be quite a lot of work … or it might be a question of tweeking a few equations and changing a few words.
I have not used tikzcd so I doubt that that part of the request that you mention, Urs, will get done. (I should learn to use it but usually get by with xy and even more restrictedly xymatrix!)
I did not mean to put off Hurkyl and would much appreciate feed back here when I have looked at the entry. No doubt I will get it if I do something outragous. Lol.
-
- CommentRowNumber27.
- CommentAuthorTim_Porter
- CommentTimeNov 5th 2021
- (edited Nov 5th 2021)
The entry does need attention. If nothing else, it refers to comonadic resolution but there is no entry explicitly on that and the entries on canonical resolution and simplicial resolution and monadic cohomology all seem to be in need of a bit of TLC. I will try to track back and do some repair work. I will probably take a fairly classical elementary viewpoint to start with, so expect some more up-to-date nPOV interventions later. :-;
I may risk duplicating some ideas, but that can be handled afterwards at the tidying stage.
-
- CommentRowNumber28.
- CommentAuthorTim_Porter
- CommentTimeNov 6th 2021
-
- CommentRowNumber29.
- CommentAuthorTim_Porter
- CommentTimeNov 6th 2021
I have started redoing the diagrams (using xymatrix as I could not get tikz-cd to work. Is there a good manual and list of worked examples for this as there is for xypic?)
-
- CommentRowNumber30.
- CommentAuthorHurkyl
- CommentTimeNov 6th 2021
Does tikz-cd just work on the site? I’ll have a go at the S[3] example
-
- CommentRowNumber31.
- CommentAuthorHurkyl
- CommentTimeNov 6th 2021
Wait nevermind, I don’t actually know how to do that S[3] example. :(
-
- CommentRowNumber32.
- CommentAuthorTim_Porter
- CommentTimeNov 6th 2021
- (edited Nov 6th 2021)
… neither do I . I understand the idea but not what those diagrams are supposed to be. (This is written out somewhere in the Menagerie notes I thought, but I cannot find the exact page!) Lets leave it for the moment. Can you improve the wording of this part? … and is what I said about opposite simplicial sets etc ok by you. By that I meana does it make sense, or are their gaps, are all the links working and do they do what you would hope they would do.
I could not find a separate entry on opposite simplicial set, but am sure I saw it the other day!
As to tikzcd I could get the triangle but not the vertical down double arrow. (I am not sure if the labels make sense but I don’t think they do in the body of the text as well.) I will leave this for tonight.
There is a bit on using tikzcd in the Lab in the How to entry.
-
- CommentRowNumber33.
- CommentAuthorHurkyl
- CommentTimeNov 6th 2021
- (edited Nov 6th 2021)
Skimming over it, everything looks fine to me. seems fine for me.
To make a double arrow, \arrow[d, Rightarrow] and similar should be the right thing, at least in a TeX document. And when you want an arrow between two vertices in a diagram where one or both endpoints don’t actually have anything drawn there… you still need to put something at that vertex or tikzcd gets confused. Just an open-brace close-brace pair works (i.e. {}).
-
- CommentRowNumber34.
- CommentAuthorTim_Porter
- CommentTimeNov 6th 2021
Thanks. I am trying to learn a bit of tizkcd as xymatrix is sometimes a bit limited.
-
- CommentRowNumber35.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2023
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeFeb 13th 2023
-
- CommentRowNumber37.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2023
I was not certain of the ’policy’ with unpublished and fairly informal items. Thanks.
-
- CommentRowNumber38.
- CommentAuthorUrs
- CommentTimeApr 26th 2023
- (edited Apr 26th 2023)
added pointer to:
- Emilio Minichiello, Manuel Rivera, Mahmoud Zeinalian, Categorical models for path spaces, Advances in Mathematics 415 (2023) 108898 [arXiv:2201.03046, doi:10.1016/j.aim.2023.108898]
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeApr 27th 2023
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeApr 27th 2023
-
- CommentRowNumber41.
- CommentAuthornLab edit announcer
- CommentTimeJul 13th 2023
-
- CommentRowNumber42.
- CommentAuthornLab edit announcer
- CommentTimeMar 29th 2024
added
- {#Arakawa23}Arakawa Kensuke, Classifying Space via Homotopy Coherent Nerve, Homology Homotopy Appl. 25(2), 2023, 373–381 (arXiv:math/2208.00550,doi:org/10.4310/HHA.2023.v25.n2.a16)
in a reference
Kensuke Arakawa
1 to 42 of 42