nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeFeb 11th 2010
I dropped a comment box over at homotopy category, since I think it might be useful to have the classical definition there, as well as make it entirely clear what "modulo homotopy" means. The only reason I didn't write it up myself is that I actually need a little bit of clarification on how to describe "modulo homotopy" as a dinatural transformation from Hom(-,-) -> [-;-]. There is a coequalizer in the first variable for each fixed second variable. Is this an end, coend, or some sort of weighted limit, etc? -
- CommentRowNumber2.
- CommentAuthorTim_Porter
- CommentTimeFeb 11th 2010
I have added a comment to your query .. BTW do sign in as Harry Gindi or whatever.
The point about the product is that in pointed spaces you need to squash the basepoint times I to a point to get things to work neatly. Alternatively, work within pairs of spaces (X,A), and use relative homotopy finishing off by restricting to A being a point.
-
- CommentRowNumber3.
- CommentAuthorHarry Gindi
- CommentTimeFeb 11th 2010
Yes, I did mean Hom(- x I, -) => Hom(-,-) (the dangers of cutting and pasting!). I plan on orderng your book once I have the money (I'm broke at the moment), but in the meantime, would you mind explaining it a little further? Also, is there any way I could buy the book (maybe an electronic copy) from you? I'd rather let you have the money than the publisher, to be honest. -
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeFeb 11th 2010
Homotopies of based spaces use smash product
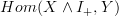 . Which is equivalent to saying, the homotopy also has to keep the basepoint fixed.
. Which is equivalent to saying, the homotopy also has to keep the basepoint fixed.I think it would probably be most helpful, pedagogically speaking, to begin with the even easier and even more classical example of unbased spaces. (-:
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeFeb 11th 2010
- (edited Feb 12th 2010)
If we take the smash product, how do we get the two maps
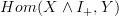 =>
=> 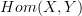 to take the coequalizer? I only said what I did about bipointed spaces because this will induce two morphisms
to take the coequalizer? I only said what I did about bipointed spaces because this will induce two morphisms  =>
=> 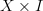 .
.How are we getting two canonical injections
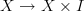 in the unbased version?
in the unbased version?I only ask this because with simplicial sets, the interval
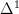 has two vertices, so it naturally has two canonical injections into the product.
has two vertices, so it naturally has two canonical injections into the product.Also, LaTeX on the n-Forum? How?
Edit: I only ask this here because I don't have Tim's book, we're not learning it in my current AT class (which has thusfar avoided any categorical language), it's not in May's book, and Switzer's book uses it without exhibiting it as an end or coend or weighted colimit related by a dinatural transformation from the Hom functor..
-
- CommentRowNumber6.
- CommentAuthorDavidRoberts
- CommentTimeFeb 11th 2010
- (edited Feb 11th 2010)
Select Markdown and put inline maths in double dollars, not single dollars. Don't worry if it doesn't come out in preview, because it works when posted (also no hard returns inside the dollars). -
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeFeb 12th 2010
Ah, thanks. Got it now.
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeFeb 12th 2010
An interval object I (in any category, based or unbased) is supplied with two maps 0,1:pt -> I. These give the injections X -> X x I -
- CommentRowNumber9.
- CommentAuthorTim_Porter
- CommentTimeFeb 12th 2010
In fact, the approach that Heiner Kamps used (based on the cubical idea of Kan before he simplicialised) is based on a cylinder functor. for which see
http://ncatlab.org/nlab/show/cylinder+functor
Our book is highly recommended!!!! some parts can be viewed online (including the pretty front cover!!!) try on google with Kamps Porter. You can decide that way if you want to spend your limited resources on it.
As the coequaliser construction is just quotienting by an equivalence relation, mentioning colimits seems a bit of overkill. Of course, you can use a cocylinder as an alternative.
-
- CommentRowNumber10.
- CommentAuthorTim_Porter
- CommentTimeFeb 12th 2010
I forgot to say that the lab entry on cylinder functor has a link to Kamps Porter.
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeFeb 12th 2010
- (edited Feb 12th 2010)
I said I'm going to order your book when I have the money! You've already sold me on it! Enough with the shameless plugs ;).
-
- CommentRowNumber12.
- CommentAuthorTim_Porter
- CommentTimeFeb 12th 2010
I like being shameless!
I will put some surveys of stuff on the Lab, but that takes time.
-
- CommentRowNumber13.
- CommentAuthorAndrew Stacey
- CommentTimeFeb 12th 2010
Of course, what really ought to happen is that Harry buys Tim's book and works through it, putting stuff on the nLab as he does so. As he does so, we (and especially Tim) yell encouragement from the sidelines.
-
- CommentRowNumber14.
- CommentAuthorHarry Gindi
- CommentTimeFeb 12th 2010
Once the summer starts, I could see putting lots of stuff on the nLab.
-
- CommentRowNumber15.
- CommentAuthorTim_Porter
- CommentTimeFeb 12th 2010
Thanks Andrew!
I have updated cylinder functor to have a link to a survey article of mine (first as lecture notes 1991, then survey paper 2003, still needing updates of references.) This may be useful. (If Harry wants to adapt some of the stuff for the lab, ..., come the summer!)
-
- CommentRowNumber16.
- CommentAuthorTim_Porter
- CommentTimeFeb 12th 2010
- (edited Feb 13th 2010)
To save a it of time, here is the link directly: Abstract-Homotopy.pdf
-
- CommentRowNumber17.
- CommentAuthorHarry Gindi
- CommentTimeFeb 12th 2010
@Tim: The link is redirecting to an empty page.
-
- CommentRowNumber18.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2010
OOPS! I will try to fix it!
-
- CommentRowNumber19.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2010
I will try this:
-
- CommentRowNumber20.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2010
I am doing something wrong (too naive!!!!). It still OOPS!
Try
http://ncatlab.org/timporter/show/HomePage
-
- CommentRowNumber21.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2010
- (edited Feb 13th 2010)
That is correct but is not `active'. Perhaps someone can tell me what I should do, as I have clearly missed some point somewhere. It looks as if I had to use a different syntax to link to my personal homepage on the n-Lab.
-
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeFeb 13th 2010
I think you have to do something like timporter:blah or timporter/blah, if I remember correctly, but Toby or Andrew can probably tell you exactly.
-
- CommentRowNumber23.
- CommentAuthorTim_Porter
- CommentTimeFeb 13th 2010
The main point should be to glance at the paper!!!! Some of it was adapted for the section in Kamps-Porter.
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMar 29th 2016
I rewrote the Idea-section at homotopy category, trying to make it less verbose, more transparently to the point.
1 to 24 of 24