nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 15th 2010
- (edited Feb 15th 2010)
I worked on improving (hopefully) and further expanding (a bit) the discussion of geometric homotopy groups at
I give at
Idea now just the brief reminder of the simple situation for 1-toposes as described at locally connected topos;
and then at Defintion I state the very obvious and simple generalization of this to homotopy oo-groupoids of objects in a locally contractible (oo,1)-topos.
Then I say something like: while this definition is very obvious and simple, it seems it has not quite been stated in the literature (except possibly in the thesis by Richad Williamson), but that there are old well-known results in the literature that essentially, with only slight modification of language, already do say precisely this.
Then I go through this claim in detail. I list three subsections with three different methods of how to construct that left adjoint
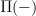 to the constant oo-stack functor, and then discuss in some detail how old and new references do already -- if slightly implicitly -- discuss precisely this. The three sections are
to the constant oo-stack functor, and then discuss in some detail how old and new references do already -- if slightly implicitly -- discuss precisely this. The three sections areYou'll notice that I also link to the discussioon of the absgtract oo-adjunction on my personal web. Currently I am thinking of the entry on my personal web as talking about the abstract notion of a path oo-groupoid, and of this page here on the nLab as providing all the "well-known" aspects of it (in that these are in the literature).
Please complain if somehow this doesn't look like the right thing to do. I am currently a bit undecided as to what bits of this discussion should be on my personal web and which on the nLab.
1 to 1 of 1