nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
Added a minor alternative rendition of the definition of natural transformation. I'm not sure that it's particularly useful for anything, but it is at least true, with some aesthetically pleasing qualities. -
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
I have an objection to this. If you see the discussion over at evil, there really isn't a very good way to define "composability" non-evilly without resorting to some black magic like type theory.
-
- CommentRowNumber3.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
The "composability" business is just my laziness out of writing "For all objects A, B, C, for all morphisms m_0 : A -> B, m_1: B -> C", etc. (or the n-ary extensions of this). It seems to me no different than any other typechecking situation in category theory (e.g., even something as basic as specifying the associativity law for composition in categories, or the existence of composites themselves); the only "equality" of objects I'm really intending to use is definitional/syntactic/presentational/intensional/whatchamacallit equality.
In other words: I wasn't proposing that one take arbitrary morphisms and then ask if they are composable. I'm just talking about taking an inhabited sequence of objects, and then a sequence of morphisms between adjacent pairs of those objects, therefore composable automatically, rather than by virtue of an evil condition to be checked after the fact. But I was just too lazy to write it out, and so wrote "a composable sequence of morphisms" instead. I could go back and rewrite it, but this feature of the wording was not essential to the ideas being presented. -
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeFeb 21st 2010
Your LaTeX is broken also =(.
-
- CommentRowNumber5.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
Whoops, that was true. I've fixed that now; thanks for pointing it out. -
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
I think you may want to reformat it as well, because it's very hard to read at the moment. It's basically a giant block of text. In particular, it might be worth it to split your diagrams out as displays. Also, please write composition in the normal way. It's really hard to follow articles that are typed up using two different notations. If you feel that strongly about it, you might be able to convince the steering committee, but I kinda doubt it.
-
- CommentRowNumber7.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
I have no strong attachment to the anti-Leibniz order for writing compositions; I only wrote it that way because I had just arrived from another page which already used it prior to me (specifically, the page on anafunctors), thus putting it in my head (as I edited both the page on anafunctor and the page on natural transformation).
I'm not sure what you mean about articles typed up using two different notations; where on the natural transformation page is the opposite convention employed? (Not that it matters; I'm perfectly willing to write it either way.) -
- CommentRowNumber8.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
Anyway, I've now rewritten the compositions (all it took was removing the semicolons [leaving composition denoted by juxtaposition instead] and swapping F and G in one line [in accord with switching to the Leibniz convention]). -
- CommentRowNumber9.
- CommentAuthorSridharRamesh
- CommentTimeFeb 21st 2010
- (edited Feb 21st 2010)
I've also gone ahead and rewritten the "for every composable string of morphisms
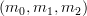 in
in  " into "for every composition
" into "for every composition 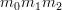 in
in  ", and the same for the n-ary case, with this hopefully now being acceptable wording for "for all objects
", and the same for the n-ary case, with this hopefully now being acceptable wording for "for all objects 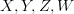 in
in  , for all morphisms
, for all morphisms 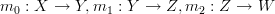 in
in  ", etc. That's all I ever meant by the original wording, anyway.
", etc. That's all I ever meant by the original wording, anyway.
1 to 9 of 9