nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 22nd 2010
started formal dg-algebra
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 22nd 2010
expanded a bit more
In the old Sullivan reference the condition for A to be formal is that there is a quasi-iso
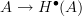 .
.In newer references, such as the survey by Kathry Hess, it says instead that there is a span of quasi-isos between
 and
and 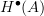 . Since in the model structure on dg-algebras all objects are fibrant, I take it that this is equivalent to saying that
. Since in the model structure on dg-algebras all objects are fibrant, I take it that this is equivalent to saying that 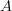 and
and 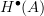 are isomorphic in the homotopy category. This is the way I state the definition now. But check if I am mixed up.
are isomorphic in the homotopy category. This is the way I state the definition now. But check if I am mixed up. -
- CommentRowNumber3.
- CommentAuthorperezl.alonso
- CommentTimeJun 19th 2025
Given the use of Sullivan models for encoding quantization/eom’s, what is the physical meaning of quantization described by nonformal spaces?
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJun 19th 2025
Let’s see. Essentially by definition it means that all Bianchi identities are of the standard untwisted form dF=0. So the system looks EoM-wise like a bunch of (possibly higher and/or self-dual but otherwise) ordinary free abelian gauge fields. Their flux quantization by a corresponding formal classifying space means to nevertheless enforce torsion-relations that may differ from those of standard free abelian gauge fields.
Is that an answer to what you are asking?
-
- CommentRowNumber5.
- CommentAuthorperezl.alonso
- CommentTimeJun 19th 2025
Sort of. In some (different) physics contexts, quasi-isomorphisms are sometimes interpreted as RG flow statements, what I was wondering is what such quasi-isomorphisms mean here.
-
- CommentRowNumber6.
- CommentAuthorperezl.alonso
- CommentTimeJun 19th 2025
pointer
- Manuel Amann. Non-formal Homogeneous Spaces (2012). (arXiv:1206.0786).
which I also added to Manuel Amann
1 to 6 of 6