nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Identify and `identification'
Bottom of Page1 to 7 of 7
-
- CommentRowNumber1.
- CommentAuthorTim_Porter
- CommentTimeFeb 22nd 2010
I would appreciate others views on the use of 'identify' in proofs. I was reading a paper recently and, having shown that a construction was independent up to isomorphism of the choices made, the author promptly said that they would identify the images of the construction thereby giving a functor. Although I must admit to using this sort of wording myself sometimes, my hackles went up. This seems a dangerous activity, identifying not raising hackles, that is. (Of course in the n-lab it is more or less evil if I understand `evil')
Does someone have a good example of when it really does miss the point, and how should one handle such situations?
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeFeb 22nd 2010
- (edited Feb 22nd 2010)
In principle, identifying is bad, but for practical purposes, it really is necessary especially dealing with things like subrings and subgroups etc. (I once wrote up a proof of the finite case of the pontryagin duality without identifying injections with subgroups. It made the proof literally three times as long as it should have been.)
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
Exactly for subobjects this may be sometimes dangerous. There are categories with examples of an object which has a proper class of nonisomorphic subobjects. But worse, some definitins, like the Rosenberg's definition of a spectrum of an abelian category simulteneously involve parts of the definition which involve classes and part which involve equality. This is in that case subtle and I have seen experts in ring theory and algebraic geometry failing to understand it just because they took one of the stands instead of literally reading the definition. I hope to soon write an entry on this, but I am trying outside of the lab doing some connection of math which I am doing to physical applications and when I come back to nlab I get distracted badly back to purepurepure math. What happened with original intentions of nlab community ? Except for discussion of TQFTs almost no physics content so far.
-
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeFeb 24th 2010
They came for the physics but stayed for the higher categories, I assume.
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
Not being a physicist myself, I never had any intention of writing about physics. (-: I can't speak for anyone else.
I'm also not sure why identifying isomorphic subobjects would be a problem simply because there are a proper class of them.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
What happened with original intentions of nlab community ? Except for discussion of TQFTs almost no physics content so far.
I intend to write more on physics. Have been intending this all along. All abstract math I write is motivated by the physics that I intend to write.
For instance I intend to eventually write a really correct POV discussion of BV-BRST. That requires derived stacks. The BV-BRST complex is precisely the global sections dg-algebra of a derived stack. It is precisely the construction in the first part of page 23 of the latest Ben-Zvi/Nadler:
there is an adjunction
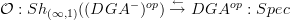
between oo-sheaves on cochain dg-algebras in non-positive degree on the one hand and unbounded dg-cochain algebras on the other. The images under
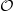 of derived oo-stacks are BV-BRST complexes: the stuff in positive degrees comes from the categorical degrees of the stack, the stuff in negative degrees from the negative degrees of the representable dg-algebras.
of derived oo-stacks are BV-BRST complexes: the stuff in positive degrees comes from the categorical degrees of the stack, the stuff in negative degrees from the negative degrees of the representable dg-algebras.Just an example where I need to get lots of pure math into place to say what I would like to say about physics.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
Apart from that it so happens that I am employed in a math department, not in a physics department. That has happened that way because the physics that I find interesting is done these days not in the physics departments. But the drawback is that I am forced to do more pure math than I would do if left entirely to my own desires.
1 to 7 of 7