nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeFeb 24th 2010
It is a bit confusing: a direct summand of an infinity groupoid. How does this look like, e.g. what is in reality a direct sum of Kan complexes ? (I don't mean the uni property but explicit description).
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
It just means: the two oo-groupoids each consist of a bunch of connected components
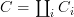 and
and 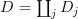 and a morphism
and a morphism 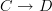 satisfies this condition if the component maps
satisfies this condition if the component maps 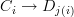 are equivalences and the function
are equivalences and the function 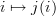 is injective.
is injective. -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
I added that to the entry, now.
-
- CommentRowNumber5.
- CommentAuthorMatanP
- CommentTimeAug 1st 2012
So in particular, in the (∞,1)-topos of topological spaces, an inclusion (even a nice one) need not be an (∞,1)-monomorphism. Do anyone here knows of a different notion for a monomorphism in an (∞,1)-topos that will include (nice) inclusions of topological spaces?
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeAug 2nd 2012
I don’t have such a good feel for that (∞,1)-category as I should, but here’s one general fact that may be relevant: in an (∞,1)-category (and already in a (2,1)-category, a regular monomorphism need not be a monomorphism. So if nice inclusions aren’t monomorphisms, they may yet be regular (or strong, extremal, etc) monomorphisms.
-
- CommentRowNumber7.
- CommentAuthorMatanP
- CommentTimeAug 3rd 2012
Thanks. I want to carefully examine the other notions you mentioned (regular, strong external), but except the nLab stubs I couldn't find any references. Can you (or someone) refer me to a place with a bit more details, i.e. other than the definition itself? -
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeAug 5th 2012
In (∞,1)-categories, I don’t know; Urs would. In 1-categories, the nLab has somewhat better coverage of the dual epimorphisms; see epimorphism#Variations for discussion of how the different forms relate.
-
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeAug 5th 2012
I think it’s misleading to talk about “the (∞,1)-topos of topological spaces”; it’s better to call it the (∞,1)-topos of ∞-groupoids. Topological spaces are a particular way to present ∞-groupoids, but a lot of information is lost in passing from a topological space to its fundamental ∞-groupoid.
In particular, every morphism of ∞-groupoids can be presented by a subspace inclusion of topological spaces, namely a relative cell complex (a cofibration in the Quillen model structure).
1 to 9 of 9