nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
am expanding the entry on smooth algebra (aka
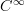 -rings, see the query box discussion there): more examples, more properties, etc.
-rings, see the query box discussion there): more examples, more properties, etc.But have to interrupt now.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
- (edited Apr 26th 2010)
Please somebody give me a sanity check on this. I ought to understand this, but I feel a little unsure that I am not overlooking something stupid.
I want to see if the forgetful functor from -rings aka smooth algebras to ordinary -algebras has a left adjoint.
Evidently the functor preserves all small limits, so I want to check if the adjoint functor theorem applies. Take the third of the three sufficient conditions listed there: should be cototal and locally small. The latter is clearly true, so is cototal?
It would seem to me that it clearly is, just as is. But maybe I am making some dumb mistake.
let be a functor, a -ring and its image under the Yoneda embedding. Then
In the integrand we have simply -many morphisms from to . So this is
This gives a left adjoint to the Yoneda embedding by .
Is that right? Am I making a stupid mistake somewhere?
-
- CommentRowNumber3.
- CommentAuthorTodd_Trimble
- CommentTimeApr 26th 2010
Perhaps I’ll need a sanity check myself, but I think the left adjoint exists on very general grounds. I think I can simplify the argument as follows:
Suppose given any morphism of finitary monads . Here will be the free algebra monad on , will be the free smooth algebra monad, and
is the inclusion which takes an -ary operation for the theory to the corresponding “smooth” -ary operation for the theory . The forgetful functor pulls back a -algebra along to obtain an -algebra .
The left adjoint takes an algebra to the (reflexive) coequalizer of the pair
living in the category of -algebras, where is the monad multiplication. This may be denoted , by analogy with tensor products.
I expect a crucial observation that this construction works is that a finitary monad (meaning a monad which arises from a Lawvere theory) preserves reflexive coequalizers, more or less because finite power functors preserve reflexive coequalizers. Followed by a longish diagram chase which is more or less the same as for an analogous argument for modules over rings. I’ll try to check this more carefully in a bit.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
I think the left adjoint exists on very general grounds.
Okay, good, that’s what I expected. Thanks, Todd.
I would have taken this as evident had not somebody who ought to be expert on this made a remark that contradicted this in some informal discussion. I figured there must have been a misunderstanding, but now I got worried that I was overlooking something very simple.
All right, thanks again.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
- (edited Apr 26th 2010)
I filled this discussion into the section The underlying ordinary algebra at smooth algebra.
Todd, please check to see if I reproduced your comment to your satisfaction. Otherwise please edit.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
Todd,
over at smooth algebra you added a query box asking for my proposed proof that is cototal. I stated that above in this thread here. Please have a look.
-
- CommentRowNumber7.
- CommentAuthorTodd_Trimble
- CommentTimeApr 26th 2010
Right, I saw in # 1 that you asked whether is cototal. Oh, I see now, you are sketching a proof; sorry. :-/ Let me have a closer look later; I want to see why this case would go through but doesn’t for the case of groups (according to Richard Wood).
-
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeApr 26th 2010
Okay, I took a look, and one problem I think I see with this formal argument is that the end you wrote down looks like a limit of a large diagram, and there’s no clear indication why it should exist in , which is small-complete. This is one of those annoying calculations where size may matter (annoying because it looks formally correct after all). The question remains whether is nevertheless cototal after all; I’d have to think about it some more.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
- (edited Apr 26th 2010)
Thanks, Tood. I appreciate that a lot.
right, size issues: but actually what I have in mind is the small site of Coo-rings, which is that of finitely generated Coo-rings only. That’s the one used in this business. I’ll add that qualifier to the Lab entry now. Wouldn’t that solve the problem? Ah, hm, then I have to argue that is still finitely generated. Hm.
I should admit that the argument here is inspired by what Bertrand Toen does around page 43 here. The adjunction he states there is precisely the one I am talking about, only that he considers k-algebras and not smooth algebras. But he has some careful universe-gymnastics earlier on. I should check that more carefully.
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
- (edited Apr 26th 2010)
Hm, I realize that I don’t understand how the size issue is actually resolved in Toen’s article either. How embarrasing.
So he invokes a universe and a bigger one containing the former. Then for him is algebras in (bottom of p. 37).
Then when he talks about that left adjoint we have been talking about, , given by on p. 43, he remarks that is not generally in . But why is it in ?? I think I am missing something here…
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
- (edited Apr 26th 2010)
Oh, now I get it. We talk there about the adjunction
Okay, never mind me, I am just being stupid. But at least I understand it now. :-)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 15th 2016
I am moving the following ancient query box out of the entry smooth algebra to here:
+– {: .query} I don't see why this is a problem; it's not like our ‘’ ever gets into a superscript. I find ‘-ring’ much more descriptive than ’generalized smooth algebra’, in fact. —Toby
Urs Schreiber: I’ll see what to do about it here. Over at derived smooth manifolds and related entried before long we’ll have to be talking about “-rings” or -rings or the like, which is not good. Also, the term “-ring” hides that it is necessarily an -algebras. Finally, the entire theory is really a special case of algebras over a Fermat theory and hence most other examples of a similar kind will by default be called algebras, not rings. For all these reasons I find “-ring” an unfortunate term. But of course I am aware that it is entirely standard.
I am not sure about ring vs algebra, however, I am for using the word “smooth” instead of the symbol . This is similar to the term “smooth map” to mean map. — Colin Tan
=–
-
- CommentRowNumber13.
- CommentAuthorTodd_Trimble
- CommentTimeNov 16th 2016
Now that this thread has been resurrected, let me return to my over-6-year-old promise in #8 to “think about it [whether is cototal] some more”, in case it is of any interest.
Unless I’m missing something, it’s not cototal. We can adapt one of the standard proofs that the category of groups is not cototal, which I’ll recall now: if it were, then every continuous functor would have a left adjoint and therefore be representable (by ). Let be a class of simple groups of cardinalities without bound. Then consider , which indeed lands in since for each group the factor is trivial as soon as and so doesn’t affect the overall product. The functor is continuous. But we cannot have for any group , else would be a retract of for all , hence would be a retract of for all , which is clearly impossible.
In the case of , we can create a large class of simple objects ( fields): if is a integral domain (meaning is injective if ), such as a free algebra on a set , then we can construct its field of fractions by taking , , and modding out by the ideal generated by elements . Let be a class of fields of cardinalities without bound, and let . The only non-trivial regular quotients of are and . If is any non-terminal object, then for all sufficiently large there is exactly one map , since as soon as the regular epi-mono factorization of such a map would have to take the form and is initial.
Then as before, form . By the same argument as before, this indeed lands in and is continuous, but is not representable (we can argue that each is a retract of , but for any object we cannot have a retract of for all , by cardinality considerations).
-
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeNov 16th 2016
- (edited Nov 16th 2016)
(Hm, maybe make that “mod out by a maximal ideal containing the elements ”.)
-
- CommentRowNumber15.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 13th 2020
-
- CommentRowNumber16.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 14th 2020
Should we rename this article to “C^∞-ring”?
What sources (if any) use “smooth algebra” instead of “C^∞-ring”?
Also, “smooth algebra” is in a serious conflict with smooth algebras in algebraic geometry (defined as k-algebras A such that Spec(A)→Spec(k) is a smooth morphism of schemes), see Eisenbud’s textbook, Section 16.7.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeDec 14th 2020
If memory serves the terminology “smooth algebra” was an invention here, to avoid clash with homotopy-theoretic -algebras, notably with the entry_C-infinity algebra_.
But if you feel energetic about adjusting it I don’t mind.
-
- CommentRowNumber18.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 14th 2020
-
- CommentRowNumber19.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 15th 2020
1 to 19 of 19