Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

• Username
• Password
• Remember me

• Sign in using OpenID
• Remember me

• Forgot your password?
• Apply for membership

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

1. • CommentRowNumber1.
   • CommentAuthorTodd_Trimble
   • CommentTimeFeb 27th 2010
   • PermaLink
   Author: Todd_Trimble
   Format: MarkdownI added a small subsection to the definition of an [[enriched category]] <latex>X</latex> over <latex>M</latex> which describes them as lax monoidal functors <latex>M^{op} \to Span(X)</latex> where the codomain is the monoidal category of endospans on <latex>X</latex> in the bicategory of spans.

   I added a small subsection to the definition of an enriched category over 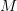which describes them as lax monoidal functors 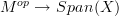where the codomain is the monoidal category of endospans on in the bicategory of spans.

2. • CommentRowNumber2.
   • CommentAuthorTodd_Trimble
   • CommentTimeFeb 28th 2010
   • PermaLink
   Author: Todd_Trimble
   Format: MarkdownI couldn't find any explicit definition of this on the [[enriched category]] page, so I put in a section on enrichment in a bicategory.

   I couldn't find any explicit definition of this on the enriched category page, so I put in a section on enrichment in a bicategory.

3. • CommentRowNumber3.
   • CommentAuthorMike Shulman
   • CommentTimeMar 2nd 2010
   • PermaLink
   Author: Mike Shulman
   Format: MarkdownThanks. I added another section about enrichment in a double category.

   Thanks. I added another section about enrichment in a double category.