Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: Two questions on the category QChan

Bottom of Page

1 to 6 of 6

  1.  
    • CommentRowNumber1.
    • CommentAuthorIan_Durham
    • CommentTimeMar 1st 2010
    • (edited Mar 1st 2010)
    I'm still pretty new to nLab and I want to make sure I get the right etiquette, so if this type of question isn't appropriate for n-Forum, please let me know.

    On the page on quantum channels, Urs defined the category QChan. Presumably we can make a subcategory (actually several of varying dimension, I would think) of QChan with the objects of the subcategory being the set of linear operators on the vector space of QChan. In Awodey's book on category theory he notes that a category is small if both the collection of objects on the category as well as the collection of arrows on the category are sets. Given that definition, it would seem that the subcategories of QChan that I mentioned are "small." Does that make sense?

    Also, would it make sense to assume that, since the tensor product is a functor, we could make a commutative square using a couple of these subcategories (if that's the right wording) and thus have an arrow category of QChan?

    Thank you!
    • CommentRowNumber2.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 1st 2010
    I think the general idea is that one asks a question at the appropriate point on the page (in a query box) and then puts a comment here that you asked the question, with a link.

    findimVect is not a small category, but is equivalent to one. This may help for starters.
    • CommentRowNumber3.
    • CommentAuthorIan_Durham
    • CommentTimeMar 1st 2010
    OK, thanks. I did put a query on the page about my first question. I'll put the second question in there and folks can go there to answer it. Thanks for the help!
    • CommentRowNumber4.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 1st 2010
    • (edited Mar 1st 2010)

    Replied at quantum channel.

    Reading both questions together (here and on the lab) I think that your question about commutative squares is asking whether you can take the arrow category 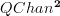QChan^\mathbf{2} and consider subcategories of this defined using subcategories of 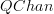QChan. Am I near the mark?

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeMar 1st 2010

    I have replied at the entry

    it would seem that the subcategories of QChan that I mentioned are "small."

    I may not understand which subcategories are meant, but clearly Qchan itself is small, so all its subcategories are necessarily small.

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeMar 1st 2010
    • (edited Mar 1st 2010)

    I should maybe clarify: the way I defined 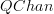QChan over at the entry it is manifestly a small category . But of course what I define is equivalent to various other definitions that one would want to write down. Instead of talking about n x n -matrices, we could be tallking about linear endomorphisms of arbitrary n-dimensional complex vector spacess. That would give, as David say, a definition of QChan that is at least essentially small .

    There are various other generalizations that one can consider. However, I feel the discussion would profit from first focusing attention entirely to the simple setup of 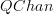QChan as it is currently defined in that entry. Once we all agree -- and Ian agrees -- about what is going on there, I am willing to consider more sophisticated versions and discuss them.

1 to 6 of 6

  1.