nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 1st 2010
started rational homotopy theory in an (infinity,1)-topos
With just slightly more it could also be called "Lie theory in an oo,1-topos" I suppose.
if you looked at this yesterday, as it was under construction, maybe have another look: I believe I could clarify the global story a bit better.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
- (edited Mar 2nd 2010)
If for the monad that Toen/Ben-Zvi/Nadler call "affinization"
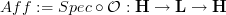
instead I write
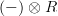 , in view of Toen's theorem on rationalization which shows that
, in view of Toen's theorem on rationalization which shows that 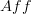 is really the
is really the 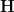 -internal version of rationalization
-internal version of rationalization 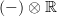 on
on 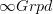 , then the Chern character characteristic class on
, then the Chern character characteristic class on 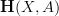 lands literally in
lands literally in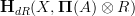
(as on my page), and thus looks essentially literally like the Chern-character map as defined for abelian Eilenberg-Steenrod cohomology theories where A is a spectrum.
-
- CommentRowNumber3.
- CommentAuthorAndrew Stacey
- CommentTimeMar 2nd 2010
Many apologies for this, but I just upgraded instiki to the latest major version while you were editing this page a few minutes ago. I don't think that anything went wrong, but because you were editing it then I don't have a previous version to check against. Just do a sanity check on this page to make sure that your last edit registered properly - if anything did go wrong then it'll be really obvious, like the edit not happening or special characters getting completely mangled. So if it looks okay, I'm pretty sure that it is.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
Thanks, Andrew. Everything looks fine.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
Did you do something again, Andrew? I just mysteriously lost my last edits to my personal web...
-
- CommentRowNumber6.
- CommentAuthorAndrew Stacey
- CommentTimeMar 2nd 2010
Not that I know of.
I've just been poking around in the logs. You seem to have been editing two pages recently on your web. The history page for the main one (structures in a ...) seems to reflect what's been going on in the logs.
What exactly happened? Did you edit a page, see the edits, and then have them disappear? Or did you edit a page, and then next time you checked the edits weren't there? The first is more serious, the second could be down to the "save" request not getting through to the server (and can be if you're editing in one window but did the check in another without realising that you hadn't saved the edits from the other.)
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
Maybe I simply managed to trick myself. I think I wrote the section "Hochschild cohomology" at "structures in..." and saved it. Then when I looked next time it wasn't there. But maybe I managed to confuse myself.
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeMar 4th 2010
- (edited Mar 4th 2010)
added to the beginning of this section a clarifiying remark on how Toen's presheaf
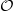 is the one represented by the line object
is the one represented by the line object 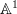 .
. -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeApr 26th 2010
added to the discussion of Toen’s Champs affine the necessary (and previously missing) size-gymnastics on the categories of algebras used in the section on Toen’s setup.
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeMay 20th 2010
in the entry rational homotopy theory in an (infinity,1)-topos I had had a remark saying that it seemed to me that Toen actually shows that cosimplicial algebras form a reflective sub-(oo,1)-category of oo-stacks on algebras^op on precisely those objects that are local with respect to morphisms that induces isos in k-valued cohomology, where k is the ground algebra.
Now I finally noticed that this observation of mine is in fact a theorem in Toen’s article, namely 2.2.9, p. 48. Silly me.
So I now removed the query box on this and instead put in the statement of the theorem at the end of this section.
1 to 10 of 10