nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorrdkw10
- CommentTimeMar 2nd 2010
Can anyone explain how to show that a $G$-torsor is homeomorphic to the group $G$ itself? -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
quite generally G-torsors (over the point) in a cartesian category C are isomorphic to G
I wrote this as an abstract argument here: torsors -- Properties This gives what you are asking for when
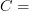 Top.
Top.But in components the argument is pretty trivial: take the defining isomorphism
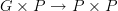 and fix any one point in the first copy of P. Then this induces an isomorphism
and fix any one point in the first copy of P. Then this induces an isomorphism 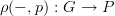
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
I have further expanded the Idea-section at torsor to amplify that this is really a defining property of torsors.
-
- CommentRowNumber4.
- CommentAuthorrdkw10
- CommentTimeMar 9th 2010
Ok, thanks a lot. I will start looking :) -
- CommentRowNumber5.
- CommentAuthorTim_Porter
- CommentTimeSep 10th 2010
I have been checking the definitions of torsor (for various applications) and note that the definition on the lab gives uniqueness of the groups element concerned as part of the definition of transitive, yet most sources use transitive (as applied to group actions) to mean :
Given x,y in the set, there is some element g∈G such that g.x=y, i.e. that there is but one orbit.
Transitive plus free is then to imply that the element g is uniquely determined by x and y, but without ’free’ one does not have uniqueness.
We thus seem to have that the n-Lab ’transitive’ is the usual regular or principal, (even without the ’free’ part of the definition). Am I getting confused? It certainly is confusing as it stands, so help please!
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeSep 10th 2010
That’s an error in the clause on transitivity. I have now removed the word “unique” there.
-
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeSep 10th 2010
That’s an error. It should be
transitive: for every two points in (a fiber of) the space, there is an element of the group taking one to the other.
Actually, the page should state the definition at least somewhere as:
for an object X and a group object G in a category C (with finite products) with X a (left) G-object with action map a:G×X→X, X is a G-torsor if and and only if the canonical map (a,pr2):G×X→X×X is an isomorphism in C.
but I can’t edit due to the spam filter.
Another formulation is this (again working in C)
an object X is a G-torsor if there is a discrete fibration of internal groupoids codisc(X)→BG. This is the viewpoint used by Duskin and Glenn on K-torsors for a simplicial group K.
-
- CommentRowNumber8.
- CommentAuthorTodd_Trimble
- CommentTimeSep 10th 2010
The language has gotten a little confused in this article, since we are supposed to be working in a “cartesian closed category” C (why? and what about pullbacks?), and we have this supposed magic ability to pick points, which we can’t do in this generality.
I’m going to try reworking the article, and I’ll post again here when I’m done (which may be a few hours, alas).
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeSep 10th 2010
Thanks for taking care of this, Todd.
Ideally we’d get the entry to the point where it covers also torsors in sheaf toposes and principal bundles.
-
- CommentRowNumber10.
- CommentAuthorTodd_Trimble
- CommentTimeSep 10th 2010
Okay, I’ve finished for the time being. I don’t claim the article has been optimized, but I think some points have been clarified and have a general scope. Please take a look.
-
- CommentRowNumber11.
- CommentAuthorTobyBartels
- CommentTimeSep 11th 2010
Yes, good work Todd.
I can’t see anywhere where the closed structure is used, and since we want to apply this to Top (which is not closed cartesian), I have removed that word.
-
- CommentRowNumber12.
- CommentAuthorDavidRoberts
- CommentTimeSep 12th 2010
I agree - we shouldn’t need cartesian closed, just cartesian. And as far as points are concerned, we just need that instead of
transitive: for every two points in (a fiber of) the space, there is an element of the group taking one to the other.
we should have
G×X→X×X is an epimorphism (of the appropriate variety) e.g regular
-
- CommentRowNumber13.
- CommentAuthorTim_Porter
- CommentTimeSep 12th 2010
@David: I’m not sure if you are ’right’ pedagogically. The ’offending statements’ are in the ideas section and for getting the idea of torsors, using elements may be useful there. In the body of the entry, various things about generalised elements are said and the definition involving the isomorphism between G×X and X×X is given. Perhaps your point about transitivity should be made at the entry on actions, so that the well known form of ’transitive action’ is given, then interpreted, first in categorical terms as you suggest and then from the nPOV. (I sometimes think that some entries may jump too quickly from the classical way of looking at things straight to an nPOV approach and this may be too big a jump for the debutants in this area.)
Whilst on the subject of torsors, I have been trying to find a ’good’ clear, easy, and elementary treatment of the translation of intuitions between group extensions and torsors. Does anyone know where one is ’in the literature’? (My access to the literature is now quite limited, so ’online’ would be great.) Perhaps this might be a good thing to add as an example within the entry on torsors. Approaches using classifying spaces are ‘out there’ I know but I feel that someone must have given a more simple minded elementary approach (suitable for me :-)).
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
- (edited Sep 12th 2010)
The ’offending statements’ are in the ideas section
Which ones are they?
Perhaps your point about transitivity should be made at the entry on actions, so that the well known form of ’transitive action’ is given, then interpreted, first in categorical terms as you suggest and then from the nPOV.
By the way, what happens when you hit the edit-button? :-)
(I sometimes think that some entries may jump too quickly from the classical way of looking at things straight to an nPOV approach and this may be too big a jump for the debutants in this area.)
There is a simple explanation for this and other expository deficiencies: those who edit entries mostly do add material they themselves are interested in, not so much as a general public service to the rest of the world. I may not currently (not as long as somebody makes me give a course on it) myself benefit from writing an exposition of standard concept A, but for my own research I might profit a lot from explaining to myself concept ∞A. So then that appears on the nLab.
I run into entries that I find unsatisfactorily incomplete all the time. One thing that helps is: to edit them. I found out that one thing that does not work so well is to ask others to edit what I find unsatisfactory.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
I tried to polish a bit more:
added formal Definition-environments in order to structure the different aspects in the Definition section more clearly.
added Examples-subsection to disentangle the different examples more clearly. There was an orpahned sentence at the end of the Introduction saying something like “To deconstruct this we now assume we are in a sheaf topos”. I removed that sentence at the end of the introduction, where it didn’t fit. Also, there is an Examples-part (now a subsection) on torsors in sheaves, which currently has no real content. Maybe somebody wants to add some stuff there.
created a section Generalizations that rescues two remarks that were drowned in the list on references.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
Oh, and I added the example of units of measurement as torsors in Set! :-)
-
- CommentRowNumber17.
- CommentAuthorTim_Porter
- CommentTimeSep 12th 2010
By ’offending’ statements I meant the ones which referred to elements that David had noted in his comment (No 12).
I understand the dual purpose of the lab both as a front end for nPOV ideas for the ’outside’ world and for exploring (with the help of others) ideas that need clarifying in our own minds. That is precisely why I need the torsor - extension transition to be clear in my mind (and it is not yet!). I need to bridge a gap between the approach to Schreier theory that Ronnie and I looked at in a paper a long time ago and the bitorsor approach of Larry Breen. This is partially to handle a case where the straightforward generalisation does not work (namely profinite groups where automorphism gadgets are very hard to define) but also to tie together some of my ideas mentioned in the Menagerie…. which I must get back to!
I would edit if I could see what to say :-( but I am often not even partially sure. (Also it is said that there are only 48 hours in a day and 10 days in a week! It sometimes seems like that.)
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
- (edited Sep 12th 2010)
translation of intuitions between group extensions and torsors. Does anyone know
Are you referring to thinking of a group extension A→ˆG→G as defining an A-torsor over G?
We have remarks on this in various entries, but likely not in the form you are looking for. But what we have are discussions on how group n-cocycles are the same as ∞-functors BG→BnA and how the principal ∞-bundles that these classify are the corresponding extensions exhibited by the induced fiber sequences
⋯→Bn−1A→BˆG→BG→BnA.Actually, with just the bare minimum of ∞-groupoid theory this is quite elementary.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
-
- CommentRowNumber20.
- CommentAuthorTim_Porter
- CommentTimeSep 12th 2010
- (edited Sep 12th 2010)
Thanks. I will check those out. Sometimes the generality helps a lot sometimes less so.
….
Yes, that gives me exactly what I thought was the case. It was a simple as I thought, but somehow it does not seem to be often used as a means of getting the various perspectives on torsors across. I must not reread what the entry goes on to say!
-
- CommentRowNumber21.
- CommentAuthorTim_Porter
- CommentTimeSep 12th 2010
You mentioned the edit button just now. Can I inquire why?
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
- (edited Sep 12th 2010)
Hi Tim,
you write:
You mentioned the edit button just now. Can I inquire why?
Maybe this is a big misunderstanding, but to me your comments on this thread here came across as if you continued to suggest that some of us should implement in the entry improvements that you found necessary.
You started out with pointing out an obvious erroneous adjective. But then it was me who had to go to the entry to remove that adjective. Then afterwards you seemed to suggest that this and that should be done to the entry. Since none of these improvements are likely to be controversial, I am trying to suggest to you that it would be much more efficient for all of us if you simply hit the edit button of the entry and made the edits that you propose. I think even if you are time pressured, it takes about the same time to make these edits in the entry as it does to explain here on the nForum to us what you think the edits are that should be done. Probably less.
I apologize if this is a misunderstanding on my part. But this is the impression I was getting here. So in summary: I want to suggest that you should feel encouraged to edit improvements into any entry as soon as you see a possibility to do so.
-
- CommentRowNumber23.
- CommentAuthorTim_Porter
- CommentTimeSep 12th 2010
I understand your point, but I find that I am very uncertain on this particular topic area and so hesitated to correct/edit. For instance, I am looking at Baues Wirsching cohomology because I really need a detailed non-Abelian version and have been experimenting with various aspects of it. I spent a long time hesitating about Baues’ definition of linear extension of categories as he uses the term ’effective’ yet that does not tie in with the sense of that term elsewhere. I realised after several days that what he said was effective was what I would call ’free’ and that cleared up the difficulty. I find it hard to realise sometimes that someone uses terminology so differently, and am reluctant to ’correct’ it in case I have just not understood something subtle!
I rely on the web for most things as I have no facilities in Bangor to speak of (since they shut us down) and only the books and papers that are in our house, so sometimes I am stuck. (End of ’woe is me’ section! :-))
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
One addendum to group extensions:
the proof that for c a an abelian group 2-cocycle on G the corresponding extension A→ˆG→G is just the delooping of the homotopy fiber of the cocycle regarded as a 2-functor c:BG→B2A is precisely the same proof as that spelled out in some detail at bundle gerbe showing that a bundle gerbe is a model for the total space of a BU(1)-2-bundle.
Indeed, it is literally and precisely the same pehnomenon and same argument in both cases: the delooped group extension BˆG is precisely the bundle gerbe over BG classified by the Dixmier-Douady class BG→B2U(1).
And all this remains true for nonabelian group extensions and nonabelian bundle gerbes. This is described a bit at nonabelian group cohomology.
-
- CommentRowNumber25.
- CommentAuthorTodd_Trimble
- CommentTimeSep 12th 2010
Tim wrote:
I rely on the web for most things as I have no facilities in Bangor to speak of (since they shut us down) and only the books and papers that are in our house, so sometimes I am stuck.
My sympathies; I have been in this situation for years now. This is a huge reason I am interested in the success of the nLab: knowledge freely available to all.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
- (edited Sep 12th 2010)
This is a huge reason I am interested in the success of the nLab: knowledge freely available to all.
This reminds me: here in Vienna, the other day Alan Carey asked me for suggstions for referees on some topic that is being discussed at the Manifold Atlas-wiki.
I hadn’t known before that they are being that serious about this wiki. Alan says the plan is to have a fully reliable wiki-source for theorems and results than can be cited, motivated by the observation, he says, that there are too many mistakes on Wikipedia.
I am just wondering how they will handle re-edits. For suppose some entry is marked as “refereed” at some point, and then later it is edited again. Presumeably edited in order to improve it! So what now?
I am also wondering about the following: one unfortunate thing about standard refereeing is its distinction between author and referee. The natural process is different: if I read somebody’s notes or nLab entry, say, and come across an imperfection that I recognize, then I build on his or her work and just add my correction or remark right away. This is refereeing and authoring at the same time. The distinction between referee and author is what makes much of the standard refereeing process such a pain: the referee who should be enthusiastic about working on the problem under discussion has his hands tied up.
I am not sure how practical it actually is, but maybe we should think about the following: the edit-history of any nLab entry is already recorded. If we would agrree that everyboy who re-edits and then submits an entry approves of the full entry in the form in that he submits it, then that is a refereeing decision. You could then go to any nLab entry, look at the edit history and see the list of people who did “referee and author” this article.
Well, I think this actually already pretty much the way it works here.
-
- CommentRowNumber27.
- CommentAuthorEric
- CommentTimeSep 12th 2010
Well, I think this actually already pretty much the way it works here.
I second that.
-
- CommentRowNumber28.
- CommentAuthorTodd_Trimble
- CommentTimeSep 12th 2010
Those are good points. Did you mention them to Alan?
Well, I think this actually already pretty much the way it works here.
Pretty much, but there are always so many imperfections on pages that it would be hard to get me (for example) to fully assent to “I approve of the full entry in its present form”, because that seems too definitive. I am quite conscious of the tentative state in which I leave things even after repeated edits, and rarely do I quite “approve” of anything!
Anyway, I think the system we have works about as well as we can expect it to.
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeSep 12th 2010
- (edited Sep 12th 2010)
Pretty much, but there are always so many imperfections on pages that it would be hard to get me (for example) to fully assent to “I approve of the full entry in its present form”, because that seems too definitive. I am quite conscious of the tentative state in which I leave things even after repeated edits, and rarely do I quite “approve” of anything!
Yes, I fully agree. But there is maybe a distinction to be made between
“I can confirm that nothing in this entry, incomplete as it is, is outright wrong”
and
“this entry is now in a shape that it can serve as a definite reference on its topic”.
(The same really applies for published articles just as well, but that’s maybe a different story.)
-
- CommentRowNumber30.
- CommentAuthorTodd_Trimble
- CommentTimeSep 12th 2010
I guess you intend that the first choice is the weaker choice? Because I think I would even have trouble there!
Essentially, such confirmation would place me in the position of actually being a referee who takes his job seriously. I do take what I do here seriously, of course, but oftentimes edits might be quite localized. I try to format them so that the terminology and notation agree with the rest of the article, and I try to respect the spirit of the rest of the article, but I don’t always scrutinize the article as a whole. That might be because I am nowhere near to understanding the article, but I see something that looks confusing to me or that I think could be clarified, some piece I do have some understanding of. In such a situation, I would be unable to confirm there are no outright errors anywhere.
-
- CommentRowNumber31.
- CommentAuthorTobyBartels
- CommentTimeSep 12th 2010
-
- CommentRowNumber32.
- CommentAuthorMike Shulman
- CommentTimeSep 14th 2010
I second Todd #30. At the extreme end, often when I’m reading a page that I don’t (yet) understand, I will nevertheless take it upon myself to fix obvious typos; obviously this should not be interpreted as any sort of confirmation of correctness for the article! But also, as Todd points out, even a substantial edit to one section of a long page may not (and, I think, should not) imply that I’ve even read the rest of the page.
-
- CommentRowNumber33.
- CommentAuthorEric
- CommentTimeSep 14th 2010
@Mike #32
A quick comment from the vortex that is my day job…
But what we have is even better than this.
We can look at the history of any page and see not only that Mike or Todd or Urs modified the page, but we can see the actual changes they made.
I think it is fair to say that if YOU add something, then what you added has your blessing.
Back to the vortex (and apologies if this is completely irrelevant to the point you’re making)…
PS: It would be neat to have the ability to give sections of pages blessings more explicitly somehow. Perhaps via comments when making an edit? It is common in version control to be able to add a comment to a version. For example, if you simply fix a typo, you would add a comment, “I fixed a typo, but the rest of the page looks bogus. Need to revisit.” Then others coming along later can see a history of comments for each version.
-
- CommentRowNumber34.
- CommentAuthorTim_Porter
- CommentTimeSep 14th 2010
@Eric I have been using svn in some collaborative work with Philippe Malbos and Yves Guiraud. (This is version control software with a central depository of all the versions, in case you have not met it.) For each post we have the possibility of leaving a comment for the others. This is VERY useful. No comment is required and much of the time that part is left blank, but, just as in the n-Lab, someone may feel that the others should look at a revision or new section as the author is not 100% happy with it. Perhaps the forum could be more used in this way. Urs and Zoran already do use it so and that is instructive, but minor comments are not always mentioned by others.
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
- (edited Sep 14th 2010)
Todd, Mike,
just for the record, I don’t think there is a disagreement:
in #26 I remarked on the suggestion that one could agree that an edit implies a blessing of the entry in that stage:
I am not sure how practical it actually is,
Then after I had written that paragraph I had thought about it and found that practical or not, in many cases it does work this way here in practice, so I concluded with the sentence
Well, I think this actually already pretty much the way it works here.
I should have formulated that better. I was just thinking of the fact that clearly we have given each other quite a bit of critical feedback here on bits of entries.
See, the motivation for this thought was that I was wondering if one can establish a situation where a wiki is formally “peer reviewed” without going through extra yoga wih extra software.
But maybe the answer is simply: no, it is not practical. But I was wondering about it.
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
- (edited Sep 14th 2010)
One more thought: it might still be easy to establish a functionality that allows me IF I wish to indicate that I checked an entry, to have that version marked as such.
For instance, maybe next to the buttons “SUBMIT” and “CANCEL” in the edit window, there could be a third button “SUBMIT AS REFEREED”, clicking on which will have the usual effect, plus setting a simple flag in the entry’s history.
-
- CommentRowNumber37.
- CommentAuthorTim_Porter
- CommentTimeSep 14th 2010
@Urs Usually a journal referee can only give a view that something is ’fine’ and appropriate for the journal, a refs report is not an IMPRIMATUR. For us, perhaps a button saying ’submit: fixed typo’ would be more useful. The Lab is being used as a source of ideas, concepts etc, and already has a ‘health warning’ to some extent saying that the entries are to be taken as they are, and do not pretend to perfection, and it is of its nature to be changing and fluid. Please don’t try to make it more rigid than it needs to be.
Regular contributors and readers should be encouraged to note HERE anything other than minor changes, and if a typo has been fixed, a category TYPO in the Forum could be used to signal that the change (as listed in recently revised) is a minor one. I think the present system works well and no major change is needed but some of us (myself included) need to use its functionality better! :-)
-
- CommentRowNumber38.
- CommentAuthorEric
- CommentTimeSep 14th 2010
I’ve voice my opinion a couple of times that each page on the nLab should point to a “Discussion” thread here on the Forum.
If someone is already familiar with the n-Family, they know to come here for comments, but someone stopping by the nLab for the first time might like to know that there is likely an entire thread on the nForum discussing that page.
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
- (edited Sep 14th 2010)
Please don’t try to make it more rigid than it needs to be.
I don’t.
I just think about adding a service to the rest of the world: if we have an entry with good and useful information that people might want to cite in their research articles, but don’t because they don’t know how reliable it is, then we could offer the service of providing the information that this content has been checked and found sensible by xyz and abc.
-
- CommentRowNumber40.
- CommentAuthorTim_Porter
- CommentTimeSep 14th 2010
I was not intending to imply that you were making it rigid, but that a refereeing system might push things a bit that way and that would be a pity.
There may be another reason why people might be reluctant to cite the Lab and that is that the entry that they liked and used has since changed! We hope that it would be
for the better' but not everyone will agree by the very nature of human beings! Perhaps ausers guide’ would help, so that an indication of the stability of an entry would be easily accessible to the potential ‘citer’. If an entry is changing often then they should perhaps wait and see what happens to it. Parts of the Lab are reasonably stable, others are bubbling nicely! :-)Perhaps we should in our own articles make crossed references to the lab but we need to work on the wording we use. I have tried something like: For a discussion of the theory including a development and further references see ….’ This may not be optimal however.
I suspect that most books are not refereed for the accuracy of the proofs and definitions. When I have been asked by a publisher to look at a text the task is clearly indicated to be to evaluate the work for suitability, level, etc. The accuracy is the responsibility of the author.
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
I was not intending to imply that you were making it rigid, but that a refereeing system might push things a bit that way
I don’t think anyone here would feel inhibited to work on the nLab only because I declare that I think some entries are actually correct!
There may be another reason why people might be reluctant to cite the Lab and that is that the entry that they liked and used has since changed!
Citations would have to go to the date-stampted version in the history list. Same is already true for arXiv-citations, for instance.
-
- CommentRowNumber42.
- CommentAuthorTodd_Trimble
- CommentTimeSep 14th 2010
I suppose citation of an nLab entry could go so far as to cite the revision number preferred by the author.
How much do people cite wikis, anyway? Or maybe the question should be: how reliable or useful do people find the nLab? Toby once said that the nLab is basically a mess, and I think he’s absolutely right, and perhaps that’s even the nature of the beast, but I’d be interested in honest opinions of those outside the relatively small group of contributors. Of the comments I’ve heard so far, many have tilted to the negative.
There is a small (very small) percentage of non-stubby pages that I’d be willing to vouch for in terms of “no outright errors”.
-
- CommentRowNumber43.
- CommentAuthorTodd_Trimble
- CommentTimeSep 14th 2010
I’d better qualify that last comment. I would hate, hate, hate to have for example the MO system “vote up, vote down” as a gauge of what nLab pages people like. In dark moments, I really do feel that “people” are, on average and en masse, not-very-bright sheep. >: - ()
-
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
How much do people cite wikis, anyway?
If they would already cite wikis routinely, we wouldn’t be having this discussion. Would we?
I thought the Manifold Atlas-example shows that there is some genuine interest in making wikis citable.
There is a small (very small) percentage of non-stubby pages that I’d be willing to vouch for in terms of “no outright errors”.
I suppose lots of people would be interested in knowing which these are. Possibly because then they might want to cite them.
-
- CommentRowNumber45.
- CommentAuthorTobyBartels
- CommentTimeSep 14th 2010
I don’t think anyone here would feel inhibited to work on the nLab only because I declare that I think some entries are actually correct!
If the current version is certified by you as correct, then a newbie may hesitate (even more than now) to edit it, lest it become incorrect. Don’t we still have the problem that category theorists are too shy to edit the nLab, even when they read it?
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
- (edited Sep 14th 2010)
A good trick to have comments both verified as well as promote adverisement for people to work on them might be that we make that little remark that the software might add read:
Joe Absentminded has seen this entry in the version from June 29 and found that there is nothing outright wrong with it. However, no entry is ever perfect. Press edit to further improve it.
-
- CommentRowNumber47.
- CommentAuthorTobyBartels
- CommentTimeSep 14th 2010
That could be a nice thing to put on the bottom of the page, where it now says “Revised on June 29, 2010 17:27:37 by Joe Absentminded (127.0.0.1)”. In the history, we’d want something shorter, but most people don’t look at the history, so it’s not so dangerous.
-
- CommentRowNumber48.
- CommentAuthorUrs
- CommentTimeSep 14th 2010
In the history, we’d want something shorter, but most people don’t look at the history, so it’s not so dangerous.
Right, so then also it shouldn’t be discouraging too many people if there were a mark in the history that Joe A. found the entry okay at some point.
1 to 48 of 48