Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Unitary operators

Bottom of Page

1 to 28 of 28

  1.  
    • CommentRowNumber1.
    • CommentAuthorIan_Durham
    • CommentTimeMar 3rd 2010
    I just added a page on unitary operators. I also have a query there about whether unitary operators on a given Hilbert space form a category.
    • CommentRowNumber2.
    • CommentAuthorzskoda
    • CommentTimeMar 3rd 2010

    They form a topological group what says it all.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeMar 3rd 2010
    • (edited Mar 3rd 2010)

    Ian, automorphisms of any object form a group, the automorphism group of that object, and if you like you can regard this group as a 1-object category. This is described at delooping.

    So the answer to your question is "yes", but it's not a particularly deep answer. It's an obvious yes.

    • CommentRowNumber4.
    • CommentAuthorIan_Durham
    • CommentTimeMar 4th 2010
    Interesting. The reason I asked (in case anyone is interested) is that I suspect that category theory might be able to help solve the problem that some quantum channels don't obey Birkhoff's theorem. If I were to "visualize" this in my head in a Venn diagram kind of way, it would be that QChan and Uni (or whatever you want to call the unitaries) partially overlap. The goal is to find a larger category (other than Vect) that encompasses them both (and preferably only them).
    • CommentRowNumber5.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 4th 2010
    • (edited Mar 4th 2010)

    There may be some diddling that needs to be done here. A priori a unitary is a (particular sort of) morphism from a Hilbert space 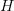H to itself (in the category Hilb). A quantum channel is a (particular sort of) morphism from the algebra 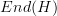End(H) to itself (in some category of algebras, maybe 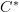C^*). The unitaries 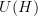U(H) of a Hilbert space act on the endomorphisms 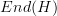End(H) by conjugation. This means we can map the unitaries into the quantum channels, but may not be one-to-one. I don't know off the top of my head if all maps from 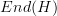End(H) to itself (of the appropriate sort) are in the image of this map, but from what you say I suspect not. The partial overlap you envisage may in fact be that one is wholly contained in the other.

    Also note that all this can be generalised to involve maps from one Hilbert space to another.

    • CommentRowNumber6.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 4th 2010

    One thing I might suggest is that we have a page called Birkhoff's theorem, or at least a page containing it. Also some detail at quantum channels at what it means for a quantum channel to obey Birkhoff's thoerem. Then we can nut out what you really need here.

    • CommentRowNumber7.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 4th 2010
    • (edited Mar 4th 2010)

    Is a quantum channel the (topological) group algebra of a unitarizable group (admits a faithful representation by a subgroup of the unitary group)? That is, instead of considering "almost everywhere vanishing" functions 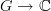G\to \mathbb{C} (the group ring), consider continuous functions 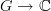G\to \mathbb{C} with compact support (the group algebra of a topological group).

    • CommentRowNumber8.
    • CommentAuthorIan_Durham
    • CommentTimeMar 4th 2010
    Hmmm. Interesting suggestion. I'll have to think about that. Check out what I wrote up for Birkhoff's theorem which gives a bit more detail about both the classical version and the suggested quantum extensions.
    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeMar 4th 2010

    A quantum channel is a (particular sort of) morphism from the algebra End(H) to itself (in some category of algebras

    Wait, a quantum channel is not in general an algebra homomorphism. Just a linear map.

    Is a quantum channel the (topological) group algebra of a unitarizable group

    Wait, a quantum channel is not an algebra, just a certain linear map.

    • CommentRowNumber10.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 4th 2010

    I dunno, I guess I read wrong.

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeMar 4th 2010
    • (edited Mar 4th 2010)

    The collection of all endo-quantum channels 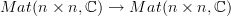Mat(n\times n, \mathbb{C} ) \to Mat(n \times n, \mathbb{C}) forms a monoid, clearly, but not even a ring, because the sum of two linear maps underlying a quantum would not be trace preserving. So also this is not an algebra.

    Unless I am missing something, of course.

    But I am puzzled: don't we all agree now on the very simple definition of what a quantum channels is the way I wrote it at quantum channel? Let me know what is unclear. Maybe I am mixed up.

    • CommentRowNumber12.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 4th 2010
    • (edited Mar 4th 2010)

    Edit: Never thee mind.

    • CommentRowNumber13.
    • CommentAuthorIan_Durham
    • CommentTimeMar 4th 2010
    I agree with your definition, though I'm curious about David's comment in which he noticed that my original intent was to have the objects be the vector spaces. I honestly don't know if that really makes a difference or not.

    But, anyway, going with the existing definition, how can we differentiate between quantum channels that are a) fully reversible, b) reversible with environmental assistance, and c) not reversible at all? A quantum extension of Birkhoff's theorem exists for a) and b) but not c). Also it is not clear (at least to me) whether all channels of type c) violate Birkhoff's theorem or just some do.
    • CommentRowNumber14.
    • CommentAuthorUrs
    • CommentTimeMar 4th 2010

    my original intent was to have the objects be the vector spaces. I honestly don't know if that really makes a difference or not.

    it makes no difference: your original intent is completely realized here.

    It makes no difference what you name the objects. There is one object per natural number 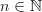n \in \mathbb{N} . And the hom-set between the object labeled 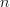n and the object labeled 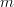m is a subset of the space of linear maps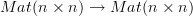 Mat(n \times n) \to Mat(n \times n)

    You can -- and probably should -- think of the object labeled n as being the vector space \mathbb{C}^n .

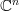    Just that morphisms between these vector spaces are not linear maps between them, but linear maps between their vector spaces of endomorphisms.

    Does that help?

    • CommentRowNumber15.
    • CommentAuthorIan_Durham
    • CommentTimeMar 4th 2010
    • (edited Mar 4th 2010)
    Yes, thanks! It actually helps a lot since I really liked your definition but wasn't sure if the idea was fully encapsulated in it (which I see it is).

    My only potential concern (and I need to check on this) is that I could see different channels, both with the same value for , having very different properties. So I'm worried that the category definition somehow washes out some of the structure. But I need to check to make sure that such a thing could actually happen (I suspect it can, but am not positive).
    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeMar 4th 2010
    • (edited Mar 4th 2010)

    My only potential concern (and I need to check on this) is that I could see different channels, both with the same value for n \in \mathbb{N}, having very different properties.

    Hm? Of course they will have different properties. Otherwise this would be a bit boring. I don't understand: what's your concern?

    Your statement sounds a bit as if you would also say: "I am concerned that there are linear maps from a vector space to itself that may have very different properties."

    • CommentRowNumber17.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 4th 2010
    Ok, I guess I was getting a little excited about describing QChan in some fancy way. Also, from the original definition (which I agree was only work in progress, and I didn't read the references (lazy!)) I thought that the maps between the matrix algebras were algebra maps.

    Some questions:

    Is it still possible to have a subspace/subalgebra/sub-thing in place of M_n(C)? In that case, we need the objects to not be just the natural numbers/C^n, but the domains/codomains of the actual arrows.

    What do you mean, Ian, about a channel being reversible with environmental help?

    In the more general channel (classical + quantum), can we replace C(X) with a general (poss. non-unital) commutative C-star algebra?

    Sorry for not posting these questions on the page - it's a bit quicker here and I'm short on time.
    • CommentRowNumber18.
    • CommentAuthorIan_Durham
    • CommentTimeMar 5th 2010
    By the way, thanks to all for actually devoting a few minutes to thinking about this. I know you're all busy, but I seriously appreciate it (and I find it to be a very stimulating discussion!).

    Anyway, let me try to explain a little better what channels are all about. A reversible quantum channel is one for which the initial state of the system - the "quantum information" - is recoverable. For some channels, recovery is really simple: just feed the output back in to the input and you get the original state back out again. For some channels, the only way to recover the original state is by plugging in the output into an entirely different quantum channel (i.e. with a different set of Kraus operators). For some channels, recovery is only possible by coupling the output to the environment (it's an open quantum system - the environment, whether or not it is quantum, has its own density operator) and then putting it through some channel (perhaps the same one). And then there are some for which the quantum information is entirely lost. Gregoratti and Werner have a basic classification for such things.

    With that said, I think I can make subcategories out of Urs' definition that would capture this structure. Does that make more sense?
    • CommentRowNumber19.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 5th 2010
    • (edited Mar 5th 2010)

    Yes. I'm curious about the channels which are their own inverses. It raises the question of channels which return the original information after passing it through n times... And in a more asymptotic mindset, for the (countable) inf. dim. Hilbert space case, how about channels which, for any small 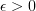\epsilon > 0, there is an N such that for all 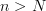n>N we are within \epsilon (in some measure of information) of the original state?

    Also, how is the 'environment' coded? By coupling I assume you mean that one tensors the output with something, and there is a channel from this tensor product back to the original state, such that there is a composite (somehow) that is the identity?

    • CommentRowNumber20.
    • CommentAuthorIan_Durham
    • CommentTimeMar 5th 2010
    Hmmm. I'm seeing two "formula does not parse" tags in your reply.

    Incidentally, just to clarify, given my newbie understanding of categories, I envisioned reversible channels were in a category whose arrows were isomorphisms while the non-reversible kind weren't, but all are clearly part the larger category QChan as Urs defined it.

    (If you guys aren't careful, you'll end up as co-authors on a paper with me...)

    Incidentally, I have a whole host of other quantum- and relativity-related things that I envision could be described by categories if anyone is interested...
    • CommentRowNumber21.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 5th 2010
    • (edited Mar 5th 2010)

    Fixed.

    I envisioned reversible channels were in a category whose arrows were isomorphisms while the non-reversible kind weren't, but all are clearly part the larger category QChan as Urs defined it.

    that is correct.

    other quantum- and relativity-related things

    Sometimes it's not so much as whether things can be described using categories (since we think everything mathematical can be described using categories, sometimes in multiple ways) but whether that adds to the understanding. The thought of a category as encoding a process or information flow is one that is helpful and useful in both QM (Coecke and collaborators) and in computer science. Describing spacetime as having the structure of a poset can be useful when describing nets of observables in algebraic quantum field theory (what Urs calls functorial QFT edit: no he doesn't, see next comment). But beware there are some things that can be written in category theoretic language which essentially is just a replacement of words, and the structure etc when written as a category is exactly the same as before with no added value. I think quantum channels (especially when the classical information and the environmental interactions are included) do have some interest, though.

    • CommentRowNumber22.
    • CommentAuthorUrs
    • CommentTimeMar 5th 2010

    nets of observables in algebraic quantum field theory (what Urs calls functorial QFT)

    Well, not quite. The net of observables is in AQFT. This is the dual concept to FQFT.

    • CommentRowNumber23.
    • CommentAuthorIan_Durham
    • CommentTimeMar 5th 2010
    Right. What I'm thinking of, actually, are physical problems where I think category might be able to help shed some light on the issue (and maybe solve a paradox or two). Otherwise, I agree that, in theory, everything could be described by categories (I was going to put a tongue-in-cheek thing on my blog describing cow's stomachs with category theory after my daughter came home from school with a book on cows that had an interesting diagram of the stomach).
    • CommentRowNumber24.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 5th 2010

    @Urs,

    my mistake :)

    • CommentRowNumber25.
    • CommentAuthorIan_Durham
    • CommentTimeMar 5th 2010
    • (edited Mar 5th 2010)
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> I realized I never fully responded to your other post.<br/><br/><blockquote> Yes. I'm curious about the channels which are their own inverses. It raises the question of channels which return the original information after passing it through n times...</blockquote><br/><br/>Yes, indeed. And I had a hunch this was potentially related to one of the proposed extensions of Birkhoff's theorem to the quantum domain partly based on the fact that both the tensor product of copies of a channel (which is equivalent to executing copies simultaneously) and compositions of a channel (which is equivalent to repeatedly feeding the output back into the input) happen to both be bilinear operations (I know that's a really vague and probably unsatisfactory response, but I'm still mulling it over).<br/><br/>I'm not sure about the asymptotic case. I'll have to go back and look at the literature again.<br/><br/>Regarding the environment, it is just tensored with the output. </div>
    • CommentRowNumber26.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 5th 2010

    So what is the environment coded as?

    • CommentRowNumber27.
    • CommentAuthorIan_Durham
    • CommentTimeMar 5th 2010
    • (edited Mar 5th 2010)
    Good question. It's always a density matrix, for one. But what form that density matrix takes all depends on the type of environment. So, for instance, in some work I've done on closed time-like curves (that is, work I've done studying them - I can't say I've ever actually been on one :)) I discovered that it actually depended on the linear map that was applied (this is one of the paradoxes of CTCs). But, in order for it to make sense it, at the very least, has to be in the same basis as the input, output, and channel themselves.

    Here's the basic model of what is called a quantum operation (and what quantum channels are basically a generalization of) for an open quantum system, i.e. one that interacts with its environment:

    Tr

    where Tr is known as the partial trace (let me know if you're not familiar with this term).
    • CommentRowNumber28.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 5th 2010

    I've not seen the partial trace before.

    I'm not too surprised (from a mathematical viewpoint) that the density matrix depends on the map, and in fact makes things interesting. The challenge is then to figure out the rules which govern this.

    I suggest that we continue this discussion at a page on the nlab, say quantum channel, in a new section about environmental interactions.

1 to 28 of 28

  1.