nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 5th 2010
- (edited Mar 5th 2010)
brief remark on my personal web on Whitehead systems in a locally contractible (oo,1)-topos.
So the homotopy fibers of the morphism
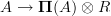 that induces the Chern character in an (oo,1)-topos are something like the "rationalized universal oo-covering space": all non-torsion homotopy groups are co-killed, or something like that.
that induces the Chern character in an (oo,1)-topos are something like the "rationalized universal oo-covering space": all non-torsion homotopy groups are co-killed, or something like that.Is there any literature on such a concept?
-
- CommentRowNumber2.
- CommentAuthorTim_Porter
- CommentTimeMar 9th 2010
I am not sure that this is closely related but your constructions do remind me of that question I asked you some time ago. In the simplicial group model it is easiest to see. You can model the n-type by a truncated simplicial group and then there is a natural fibration from the given G to that n-type. (Beware I am not being careful about whether the n-type is the n-1 type of n+1 type or whatever.) I think one can do a 'relative Abelianisation' of the fibre and get something which might correspond to chains on the universal n-covering space.
I know this best in bottom dimensions. The homotopy types you get have vanishing Whitehead products above a given dimension. The 2-crossed complexes are and example, as are Baues' quadratic complexes. The next stage down is crossed complexes and the functor from 2-crossed complexes to crossed complexes does nothing above dimension 3 and coverts the bottom 2-crossed modules to the corresponding crossed module. At the next (and last) stage the passage from crossed complexes to chain complexes over groupoids involves Fox derivative, universal derived modules etc. Ronnie has a treatment in the new book I believe, and there is a reasonably full sketch in the Menagerie.(Sections 3.2-3.4).
I have never looked at this from the point of view of the homotopy fibre as in the cases I have considered that is just the kernel.
By the way, this all goes across to simplicial commutative algebras and is related to the cotangent complex construction of Illusie.
1 to 2 of 2