nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 17th 2010
Here is where I'll put my comments on Urs' entry path oo-groupoid.
there will be both very specific comments like:
in line 5 in the Idea section I would change with and add a link to nice category of spaces. I guess stands for compactly generated, but this is never specifies in the entry, nor one finds the notation in Top, where one is directed by the present link (but one finds there).
and very vague ones, like:
in the Idea section I would add a few lines to recall that a groupoid is completely known by the category of its Sets-valued representations, i.e. by the category , and that for a (nice enough) topological space X, the category of representations of with values in Core(Sets) is equivalent to the category Cov(X) of coverings of X. Since coverigs are etale spaces of locally constant sheaves (of Sets), one knows everything about the fundamental group of X from locally constant sheaves on X. (clearly all this is implicit in the construction of in path oo-groupoid, I am just suggesting to make it a little more explicit in the Idea section, so that the reader will find something familiar to start with) -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
- (edited Mar 17th 2010)
Thanks for the comments!!
concerning the first one: I added a link to nice topological space and removed the
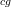 -subscript throughout. It is not of any importance there anyway.
-subscript throughout. It is not of any importance there anyway.Now I have also edited the entries Top and nice topological , in an attempt to polish them a bit more.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
- (edited Mar 17th 2010)
concerning your second comment:
okay, so I have edited that introducory paragraph a little bit,following your suggestions, to make it slightly more accessible.
-
- CommentRowNumber4.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
in Idea section
in subsection Unstructured geometric homotopy oo-groupoid, I find "If H is a locally contractible (oo,1)-topos, then we also have a left adjoint..." a bit misleading, since it seems to me that p^* having a left adjoint is the definition of being locally contrctible.
also, I would write "a left adjoint ", to continue the pattern and .
should be .
in subsection Structured geometric homotopy oo-groupoid, there's a which should be .
overall comment: in reading I find a bit hard the notation, since each time I have to remember what they are, from where to where they go, who is the adjoint of who, and on which side. I would find the much more self-explanatory, and would use it throughout the text, fixing in a remark at the beginning the geometric meaning of these functors. what I mean is that phsycologically I'm lead to think to something I read formulated in terms of upper/lower stars/shrieks as some very natural and general construction (and I feel path oo-groupoid is such a construction), while to think to something formulated in terms of functors with "their own names" as something very specific of those functors, not fitting into a simple general pattern. so I would write, for instance, instead of . Just a personal taste. -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
Thanks, these are very good points.
I'll work these in as soon as I have a second.
Concering the notation of
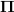 versus
versus 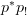 : I have thought about which one to use and found that using the specific names helps greatly to see what's actually going on. You are of course right that this notation does not amplify how general-abstract the construction is, but i found it helps to amplify the meaning of these general abstract constructions here.
: I have thought about which one to use and found that using the specific names helps greatly to see what's actually going on. You are of course right that this notation does not amplify how general-abstract the construction is, but i found it helps to amplify the meaning of these general abstract constructions here. -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
I see I said things in a confusing way: it was not versus , but versus . I like the notation a lot, and I think deserves its own symbol, since it is the main character here and since it is not an 'elementary' functor, but a 'composite' one. On the other hand, I would avoid the ubiquitous usage of and , putting their geometric meaning in the emphasis it deserves (I do think it deserves emphasis) in a dedicated paragraph at the beginning, but then letting the automatic machinery of work for you.
I have some comments on the "Relative and infinitesimal homotopy oo-groupoid" subsection, but have to go now. Should be back in three hours or so. -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
Okay, I see. I edited the entry a bit, put in the
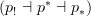 right at the beginning. Also rephrased the sentence where local contractibility is introduced. I'll see if I rename the
right at the beginning. Also rephrased the sentence where local contractibility is introduced. I'll see if I rename the 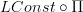 -occurences later, have to run now...
-occurences later, have to run now... -
- CommentRowNumber8.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
Section: Idea
Subsection: Relative and infinitesimal homotopy oo-groupoid
here is where I'm most confused. namely, seems to take the role that was the role of , and this makes it all a bit confusing. for instance, the sequence of morphisms is a sequence of morphisms in , but from the previous subsections one would expect and to be in .
also, the rightmost part of the first diagram in this subsection (the one with oo-Grpd) seesm to be irrelevant, and one has that bit of confusion coming from the fact that stems from but arrives into . and the motivation to rename as seems to me a bit weak: one could similarly say for any essential geometric morphism : the functor identifies points connected by a path within a fiber of in the same way as the functor identifies points connected by a finite path. but this is like renaming by for any essential geometric morphism of (oo,1)-topoi. so again I would use the classic (admittedly less evocative) notation .
summing up, I would consider an (oo,1)-topos over a base , with an essential geometric morphism, here, rather than ; would not use the notations , but would rather introduce the notations and for an arbitrary . the canonical morphism then equals on general grounds ( for any , since oo-Grpd is terminal), and does not depend on having taken an infinitesimal thickening. Finally, I would write "Of particular interest is the case where is an infinitesimal thickening of , with induced from a morphism of sites that takes a test space with infinitesimal thickening to its reduced ordinary underlying space. In this case one writes to denote the relative oo-path groupoid . Morphisms out of may be interpreted as..." -
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
on second thought, the geometry of the problem suggests me that a thickening should be a retract . This way one is allowed to consider as an object in , for in which is - I suspect - what you want.
since I feel the relative oo-path groupoid has interest on its own, I would distiguish it from the thickening stuff, to which I would devote a distinct subsection; i.e., I would have "Relative homotopy oo-groupoid" and "Thickenings and and infinitesimal oo-groupoid"
typo in the definition of : infinitsimal -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
Thanks, Domenico, very helpful comments.
I only had a handful of minutes to spare and quickly implemented what you suggested about
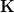 : I renamed that to
: I renamed that to 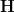 , which is indeed of course a much smoother perspective. The thing it sits over I named
, which is indeed of course a much smoother perspective. The thing it sits over I named 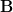 and then
and then 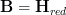 .
.Already have to run again. But thanks for the comments. Will look at this more in a little while.
-
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 19th 2010
today's comment is a bit more vague. the discussion about thickening remindem me of some discussion I recently had with Gabriele Vezzosi on virtual fundamental classes a la Behrend-Fantechi. namely, the Behrend-Fantechi ingredient to build a virtual fundamental class on a moduli space X is something they call an obstruction theory. in gemetric applications, obstructions are suggested by the geometry of the problem, an so one arrives to something which is quite natural to call "the" virtual fundamental class of X. but actually an obstruction theory a la Behrend-Fantechi can be something quite arbitrary, and different choices will lead to different fundamental classes. moreover there is no need X to be a moduli space, X can be a quite general object (now I suspect it can be an arbitrary locally contractible (oo,1)-topos).
what we had thought with Gabriele was that the obstruction theor on X had to be the datum of some algebroid (e.g., for X a smooth compact differential manifold, one would have taken the tangent algebroid, recovering the classical fundamental class; however one could have taken the 0 algebroid, and would have got 0-dimensinal fundamental calsses). the algebroid role was to say which were the "directions" in which one was allowed to move.
now I see this is precisely the role of the thickening . and also in this case the thickening can be arbitrary, but in some cases, e.g., a smooth topos, there is a canonical one.
I'll think more to this and will be back. -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
Thanks Domenico, that sounds interesting. I wasn't aware that you are in direct contact with Gabriele Vezossi. That's nice.
I am also still thinking about how to say "infintiesimal thickening" correctly. I feel like I should be able to simply put all the available ingredients together. Here is a thought:
start with some
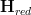 , an (oo,1)-category "of spaces" of sorts, so that
, an (oo,1)-category "of spaces" of sorts, so that 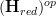 is the category of "function algebras" on these spaces.
is the category of "function algebras" on these spaces.To find its infinitesimal thickening, we should form its tangent (infinity,1)-category
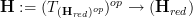 .
.Because we know from the classical case (as reviewed at module) that if
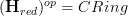 , then
, then 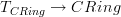 is the category of all modules over all rings, but with each module
is the category of all modules over all rings, but with each module 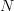 over a ring
over a ring 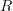 regarded as the square-0-extension ring
regarded as the square-0-extension ring 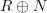 . But this is of course in
. But this is of course in 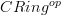 precisely an infinitesimal thickening of the space corresponding to
precisely an infinitesimal thickening of the space corresponding to 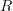 .
.Do you see what I mean?
So I am beginning to think that the tangent (oo,1)-category of an (oo,1)-topos is what gives its infinitesimal thickening. And I suppose it is no coincidence that the terms do match this way.
One technical point that i am unsure about: for
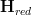 an (oo,1)-topos,
an (oo,1)-topos,is
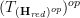 itself an (oo,1)-topos?
itself an (oo,1)-topos?is the canonical morphism
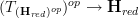 a (essential) geometric morphism?
a (essential) geometric morphism?
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
I have added some more details to tangent (infinity,1)-category.
If one looks at the cotangent-complex adjunction
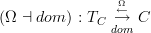
that does begin to look a bit like the infinitesimal topos-thickening
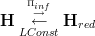
that we would like to see, using
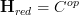 and noticing that under opposing categories left adjoint become right adjoints, and vice versa.
and noticing that under opposing categories left adjoint become right adjoints, and vice versa.But I am not sure if this can be made to work. Maybe that's not white what the relation is. But something like this might make sense.
-
- CommentRowNumber14.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 19th 2010
- (edited Mar 20th 2010)
yes. and I also see in tangent (infinity,1)-category that with and one has the retraction I was suspecting was a feature of thickening we would have liked to have.
edit: here there were a few considerations on integration as a Kan extension, but they were nonsense as in an (oo,1)-topos there is no distinction between extension and Kan extension. maybe they apply to integration in an (oo,2)-topos, but I am not going to think to this right now -
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
(sorry, I said something stupid here, which I decided to remove...) more later...
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
(second attempt, my previous one was slightly flawed...)
Domenico,
very good point about the retract.
Reminds me of the observation at my discussion of the path oo-groupoid on oo-toposes of oo-shesves on sites of "geometrically contractible objects". That makes ooGrpd be a retraxct of these beasts in a special way, which implies that these (oo,1)-toposes have the "shape" - in the sense of shape of an (infinity,1)-topos -- as the point. (Which I suppose makes good sense for these gros oo-toposes of "all spaces".)
This makes me think it would make sense if an infinitesimal thickening of such an oo-topos should still have the "shape" of the point, in particular any infinitesimal thickening should probably have the same "shape" as what it is a thickening of.
I wrote a remark on this at shape of an (infinity,1)-topos in the new section Shape of an essentialretract.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
Here is an observation:
if we start with some oo-topos of sheaves on Rings^op and then pass to its tangent oo-category, then we know that the new objects are something like pairs consisting of the old objects and a module, turned into a nilpotent ideal.
So this new tangent category might look not unlike oo-stacks on the category of pairs (rings, nilpotent ideal) which are the kinds of sheaves considered in Zoran's work with Durov, p. 22 here.
Do you see what I mean?
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
Maybe we want to be looking at this:
Let
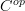 be a site and
be a site and 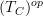 its tangent category. Then we want to put a site structure on
its tangent category. Then we want to put a site structure on 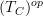 such that the projection
such that the projection 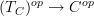 is a morphism of sites. Then this induces a geometric morphism of oo-stack oo-toposes.
is a morphism of sites. Then this induces a geometric morphism of oo-stack oo-toposes.Now, by exactly the same kind of argument that I use to show that oo-toposes are locally contractible, we should be able to see that
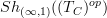 is locally contractible relative to
is locally contractible relative to 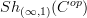 .
.This should follow when the site structure is such that sheaves on
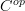 that are constantly extended to
that are constantly extended to 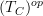 are still sheaves there, which is just what we expect of a topology on "infintiesimally thickened spaces". Then this should imply that we
are still sheaves there, which is just what we expect of a topology on "infintiesimally thickened spaces". Then this should imply that we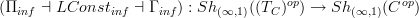 .
.Do you see what I mean? Now that I wrote this it looks to me that this should be an essentially trivial generalization of the non-relative situation discussed so far.
-
- CommentRowNumber19.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
I have to look more carefully into this but, yes, it seems things are working nicely.
there's a question which has been puzzling me all the afternoon, and maybe now I'm finally able to write it in a not too obscure way. fix a thickening of . then for every object of we have a notion of and morphisms stemming out of this are differential forms on . but now, classically, I'd like to interpret differential forms as sections of suitable powers of the cotangent bundle (or better, complex..) of . and this seems indeed to be the case, by the very definition of : it is the adjoint of and so a functor stemming from with values in is the same thing as a functor stemming from with values in , which I'd like to think as a section of "something built from and the cotangent complex of . vice versa, having a functorial notion of cotangent complex of (equivalently, of its sections) would give us a natural definition of differential forms on , and so would define a apparently without any notion of thickening.
this is still very confused, but I'm thinking of the following principle: a thickening of is the same thing as endowing each object of of a cotangent complex in a functorial way, i.e., it is giving the cotangent complex functor. even better: "thickening is taking the (oo,1)-tangent category".
so we have now to answer a few technical questions, yours: the tangent (oo,1)-category of an (oo,1)-topos is an (oo,1)-topos? projection the base is essentially geometric? and mine: do the notions of differential forms coming from the cotangent complex functor and the one coming from coincide? -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
the tangent (oo,1)-category of an (oo,1)-topos is an (oo,1)-topos? projection the base is essentially geometric?
For the time being I think it may be useful to circumvent this problem by being very slightly non-intrinsic and talking about sites:
I believe for C any site we should be able to canonically equip
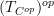 with the structure of a site such that the 0-section
with the structure of a site such that the 0-section 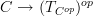 is a morphism of sites.
is a morphism of sites.For instance for the example of
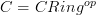 in which case
in which case 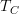 should be thought of as Mod we just take a cover in Mod to be anything which is a cover in Cring after forgetting the square-0--extensions. The "0-section" here is the functor that sends
should be thought of as Mod we just take a cover in Mod to be anything which is a cover in Cring after forgetting the square-0--extensions. The "0-section" here is the functor that sends 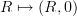 .
.My best current understanding of the resulting picture I have now indicated in the section relative theory over a base at structres in an (oo,1)-topos
(which does follow a few of your earlier suggestions)
Concerning the other point that you raise, let me think a bit...
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
Here is what I mean in the 1-categorical case
Morphisms of sites -- Examples -- Injections into tangent categories.
But check.
-
- CommentRowNumber22.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 20th 2010
I'll check. In the meanwhile I'm still distracted by differential forms. namely, in a smooth (oo,1)-topos is an oo-Lie algebroid and one obtains the algebraic de Rham complex of by taking . for a smooth affine scheme , the algebraic de Rham complex is built from Kaehler differentials, extending to a differential graded commutative algebra. so what I'm wondering is:
i) assume is an arbitrary affine scheme; can we build a natural dgca out of the cotangent complex of ?
ii) how is this dgca related to (where we thicken by taking its tangent (oo,1)-category)? -
- CommentRowNumber23.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 22nd 2010
- (edited Apr 23rd 2010)
But check.
Checked. Seems to be ok.
by the way, the coverage defined on should be the coverge induced by the coverage of via the functor ; I guess this is a general construction, but at induced toplogy there's only a hint of this. can any expert expand that? -
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
Checked. Seems to be ok.
Thanks. I wanted to write tangent category (entirely 1-categorical case) to make it fully precise. Now I realize that I need to think harder about how to correctly talk about morphisms going between objects over a different base. Still thinking...
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
Oh, wait, it is correct, I managed to confuse myself.
I am talking about the definition of morphisms at tangent category (explicit 1-categorical version). I got worried that what I wrote as the general definition of morphisms in
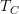 does not match the morphisms in
does not match the morphisms in 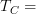 Mod when
Mod when 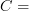 CRing. But now I think it does.
CRing. But now I think it does. -
- CommentRowNumber26.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
I agree, but to be honest I found it a bit hard to follow the proof as it is now. I would more directly define the ring homomorphism as , where is the -module homomorphism which is part of the definition of morphism in Mod, and then check that the induced morphism , which is explicitly given by is a morphism of abelian group objects over . -
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
but to be honest I found it a bit hard to read the proof as it is now
Sure, maybe this is the kind of thing best done on paper and then omitted.
a morphism of abelian group objects over
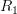 .
.Yes, but first I was worried that the pullback abelian group object as I defined it does not actually match the notion of pullback of modules. But I was just being dense, it all works of course.
Dunno, should I better remove the proof I typed again? Is it more confusing then enlightning?
-
- CommentRowNumber28.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 22nd 2010
let's try this way. I'll add the proof the way I was suggesting above into the Lab entry. then we can see what to keep of each of the two versions. on the occasion I'll adjust a few typos I've spotted -
- CommentRowNumber29.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 22nd 2010
written the first half of the proof. have to run now. will continue later. -
- CommentRowNumber30.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 23rd 2010
completed (and abridged). -
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
Okay, thanks. I removed my proof and retained yours.
All right, so coming back to the infinitesimals now.
I still need to write out a fully formal proof that the infinitesimal path oo-groupoid functor
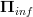 is equivalent to
is equivalent to 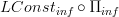 . By analogy with the finite case, for this it is sufficient to show that on representables it has the desired action, namely that it sends some
. By analogy with the finite case, for this it is sufficient to show that on representables it has the desired action, namely that it sends some 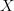 to the presheaf which takes probes of X only after reducing away all infinitesimal directions of the probe object.
to the presheaf which takes probes of X only after reducing away all infinitesimal directions of the probe object.I started typing something along these lines in the section Properties at infinitesimal interval object, but this needs to be expanded.
For the moment though I need to take care of something else.
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeApr 19th 2010
I polished a bit here and there and then expanded the discussion and the proofs in the section on the infinitesimal path oo-groupoid (on my personal web)
1 to 32 of 32