nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTobyBartels
- CommentTimeMar 20th 2010
I've written an elementary development at locale of real numbers. I think that it makes sense to me.
I also had occasion to write empty subset while I was about it.
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMar 20th 2010
This feels like a constructive version of the dedekind-cut construction of the reals (I've only seen it once in the appendix of Spivak's Calculus). Does the cauchy-sequence-approach to completion work constructively as well?
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeMar 20th 2010
The definition of point (real number) on that page is certainly a constructive version of Dedekind's cuts. (In fact, it's closer to Dedekind's original formulation than the one-sided version more often seen today.) But notice that it is the definition of open (open subset of the real line) which is the primary notion. That is not a Dedekind cut; the only similarity is that it is defined as a set of rational numbers (but actually, a set of pairs of rational numbers in practice).
The Cauchy sequence approach to defining real numbers does not work in full generality. It does work if you adopt what Fred Richman calls Weak Countable Choice, which follows from either countable choice or excluded middle. Some constructivists prefer the Cauchy sequence approach as being more predicative than the Dedekind cut approach, but otherwise Dedekind cuts seem to be better whenever it makes a difference.
I suppose that one could also take a sequential approach to defining opens from scratch. You could implicitly use the theorem that every open subset of the real line is a countable union of open intervals. But this also does not hold in full generality, at least I don't think so.
-
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeMar 20th 2010
Actually, we can make a stronger analogy between Dedekind's construction of the points in the real line and the construction here (I don't know who first did it) of the opens in the real line, like this:
The key to Dedekind's definition of point is to realise that a point is determined by the open intervals of rational numbers which it belongs to. Then it just becomes a matter of characterising exactly what information is sufficient and consistent (and in particular you realise that it's simpler to treat the lower and upper endpoints of these intervals separately, so that a point is given by an element of
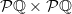 ).
).The key to this definition of open is to realise that an open is determined by the open intervals of rational numbers which it contains. Then again it just becomes a matter of characterising exactly what information is sufficient and consistent (but this time you have to treat the lower and upper endpoints of these intervals together, so that an open is still given by an element of
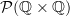 ).
). -
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeMar 20th 2010
- (edited Mar 20th 2010)
There's this notion of the completion of a group or a ring using pure category theory. Can we give a construction similar to that and using the fact that the category of sets is a complete topos (heyting or otherwise), or is that inconsistent with the internal logic of the topos?
I mean, is a nonconstructive proof in a complete heyting topos still constructive?
Edit: If the above doesn't make any sense, blame it on the fact that I've barely read any of the elephant.
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeMar 21st 2010
A proof that can be phrased in the internal language of an arbitrary topos is a constructive proof, although it might be impredicative. A proof that can be phrased in the internal language of an arbitrary Heyting category is a predicative proof as well. (Well, this depends on exactly what one means by ‘constructive’ and ‘predicative’, but they are reasonable interpretations.) I don't know what you mean by a ‘Heyting topos’; every elementary topos is a Heyting category. (And I guess that by ‘complete topos’ you mean a Grothendieck topos?)
There certainly is a sense in which
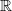 can be constructed as the completion of
can be constructed as the completion of  , although you have to specify a topology (or even uniform structure) on
, although you have to specify a topology (or even uniform structure) on  to start that, and this is valid in at least some constructive contexts (although I'm not quite sure if it works in an arbitrary topos, and I don't know how to make it work predicatively at all). That's surely got something to do with what's going on at locale of real numbers, since we are starting with the open intervals of rational numbers and ending up with the open sets of real numbers. More specifically, it has to do with the fact that the open intervals of rational numbers form a base for the topology of the real line. But I don't know how to tie it in with a general theory of completion.
to start that, and this is valid in at least some constructive contexts (although I'm not quite sure if it works in an arbitrary topos, and I don't know how to make it work predicatively at all). That's surely got something to do with what's going on at locale of real numbers, since we are starting with the open intervals of rational numbers and ending up with the open sets of real numbers. More specifically, it has to do with the fact that the open intervals of rational numbers form a base for the topology of the real line. But I don't know how to tie it in with a general theory of completion. -
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeMar 21st 2010
And if you have subset collection, then instead of Cauchy sequences you can use "Cauchy presequences," i.e. entire relations from N to Q satisfying a Cauchy condition, to get a notion which "works."
It should perhaps also be clarified a bit more what "works" means. You can define the Cauchy completion of the rationals constructively. It's just that in the absence of weak countable choice, it won't be equivalent to the Dedekind completion, and there are various reasons that the Dedekind completion is "better." For instance, a Dedekind real in the topos of sheaves on a space X is precisely a continuous map from X to the usual space of real numbers, whereas for most X, a Cauchy real in Sh(X) is much less interesting. On the other hand, one could argue that constructively, even the Dedekind completion of the rationals as a set doesn't "work," because it doesn't have the good properties of the real numbers, like the Heine-Borel theorem. That's what working with the locale of real numbers remedies.
I haven't read the page yet, but I look forward to it.
-
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeMar 21st 2010
Note: Even from the localic perspective, we still have that Dedekind real numbers are the correct points of this locale, even if the set of these points does not have a satisfactory topological structure. So localic reals (starting with opens, then points) are better than Dedekind reals (starting with points, then open sets), which are better than Cauchy reals (again starting with points).
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeMar 21st 2010
What would a very abstract definition of the locale of real numbers, along the lines of saying "complete Archimedian field"?
Something one could state in one line in the entry and then show to be equivalent to the detailed definition currently given?
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeMar 21st 2010
Good question, Urs!
Of course, ‘complete Archimedian field’ doesn't mention the topology (although it gives enough information to determine the topology, as you can tell since the result has only the identity field automorphism). But it's still a good question.
There are slicker ways to specify this locale; it's because I was having trouble understanding them that I figured out what I needed to write down the elementary definition here. But nothing close to ‘complete Archimedian field’ as far as I know.
(A pet peeve: why do so many people bother with ‘complete Archimedian field’? It's overkill! An Archimedean field is ipso facto an ordered field, but it is a theorem that a complete ordered field must be Archimedean. So isn't ‘complete ordered field’ even slicker?)
I have an added an Idea section expressing my response in #4 to Harry's observation in #2.
-
- CommentRowNumber11.
- CommentAuthorSridharRamesh
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
Perhaps people say "complete Archimedean field" to mean "terminal object in the category of Archimedean fields" rather than "ordered field which is both Dedekind-complete and Archimedean"? I mean, if you want to talk about slickness by parsimony, one could ask why people bother saying field; the terminal Archimedean group is already the reals. Etc.
Of course, all this amounts to is that there are lots of different but ultimately equivalent ways to specify (a certain conception of) the reals, so perhaps really what's going on is that people choose to explicitly state whichever defining properties they find most integral to the notion, nevermind a little redundancy. -
- CommentRowNumber12.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
Probably because most people use complete to mean cauchy-complete (clearly the more useful notion), which doesn't imply Archimedean.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
Of course, all this amounts to is that there are lots of different but ultimately equivalent ways to specify (a certain conception of) the reals,
I would very much enjoy if those -- like you, unlike me -- who know this stuff well would eventually add some kind of discussion along these lines to real number.
Eventually, what I'd be interested in is the most abstract nice characterization of the category CartSp, consisting of the real line and all its cartesian powers, with smooth maps between them. In as far as one exists.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
And what about the various characterizations of the reals as terminal coalgebras, as in On coalgebra of real numbers?
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
Can we maybe improve the first sentence in the entry real number:
A real number is an approximation of a rational number.
This sounds backwards to me: a real number is a limit of a sequence of rational numbers. So a rational number is an approximation to a real number. Clearly, no?
-
- CommentRowNumber16.
- CommentAuthorTobyBartels
- CommentTimeMar 22nd 2010
A real number is an approximation of a rational number.
Yeah, that should be
A real number is that which can be approximated by a rational number.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
Okay, I have edited the entry a bit. Please have a look. Can't do more right now, due to a shaky internet connection.
-
- CommentRowNumber18.
- CommentAuthorTobyBartels
- CommentTimeMar 23rd 2010
I want to add more to real number, but for the moment I want to explain why I changed the first sentence to ‘A real number is something that may be approximated by rational numbers.’ without any mention of sequences. In a weak foundation it is not true that every located Dedekind real number (the notion of real number that appears halfway down locale of real numbers and should appear soon on real number itself) is given by a sequence of rational numbers. I could change ‘sequence’ to ‘set’, but that begs its own foundational questions. So I think that it's simpler to just say ‘by rational numbers’ up front and give the details later.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
Okay, sure.
-
- CommentRowNumber20.
- CommentAuthorSridharRamesh
- CommentTimeMar 23rd 2010
I've made a minor edit giving a simpler description of the transformation from completely prime filters on the locale of reals to located Dedekind reals. -
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeMar 23rd 2010
Thanks for clearing that up, Sridhar.
-
- CommentRowNumber22.
- CommentAuthorTobyBartels
- CommentTimeMar 24th 2010
I split out Dedekind cut from real number so I can put a lot of details about variations in the former without cluttering up the latter.
-
- CommentRowNumber23.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
I've now put in a bunch of stuff at Dedekind cut and consider that more or less complete. I've also made real number reference Dedekind cut and locale of real numbers (remember locale of real numbers? this is a thread about locale of real numbers) more intelligently.
-
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
Now also lower reals and upper reals (just one page).
-
- CommentRowNumber25.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
Now also extended real number.
-
- CommentRowNumber26.
- CommentAuthorTobyBartels
- CommentTimeMar 29th 2010
There is discussion at real number about the Cauchy reals (most of which should probably go on a separate page, actually) and the concept of the complete ordered/archimedean field.
-
- CommentRowNumber27.
- CommentAuthorTobyBartels
- CommentTimeMar 30th 2010
OK, now Cauchy real number is pretty complete.
-
- CommentRowNumber28.
- CommentAuthorTim_Porter
- CommentTimeDec 5th 2010
- (edited Dec 5th 2010)
In the entry, near the reference to a ‘zag’ we have bi>ai+. This looks a bit strange. Is bi>ai+1 intended, or am I missing something. (I was just browsing… as one does… and noticed this. :-)) There are several uses of the notation but it miught just be ’copy and paste’ errors rather than something deep.
-
- CommentRowNumber29.
- CommentAuthorDavidRoberts
- CommentTimeDec 6th 2010
My guess is that i+ is the intended subscript, as some form of notation for a constructive successor.
-
- CommentRowNumber30.
- CommentAuthorTobyBartels
- CommentTimeDec 6th 2010
It is indeed a superscript within the subscript; i+ means the successor of i, which is indeed equal to i+1 (but shorter and more fundamental). It’s not particularly constructive, nor is it due to me, but I like it.
-
- CommentRowNumber31.
- CommentAuthorTobyBartels
- CommentTimeDec 6th 2010
H’m, I just realised that the definition of open on this page is wrong! That may explain why I never fully proved some of the theorems …. I’ll fix the definition now.
1 to 31 of 31