Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration finite foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf sheaves simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: Boundary maps in the simplex-category?

Bottom of Page

1 to 20 of 20

  1.  
    • CommentRowNumber1.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 23rd 2010
    • (edited Mar 23rd 2010)

    So right now in my formal classes, I'm doing homology, and it looks to me like singular homology is just the homology of the complex:

    \ldots FSing(X)_n\to FSing(X)_{n-1}\to\ldots\to FSing(X)_0.

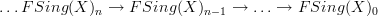    However, it's not clear to me how to use maps 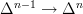\Delta^{n-1}\to \Delta^n to induce the boundary maps functorially using Yoneda. Is there any way to do it, or am I doing something that won't work? (note: F denotes the free abelian group on that set.)

    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeMar 23rd 2010
    • (edited Mar 23rd 2010)

    The step you need is the Dold-Kan correspondence: what we get naturally from the boundary maps is a simplicial abelian group

    \cdots \stackrel{\to}{\stackrel{\to}{\to}}F Sing(X)_1 \stackrel{\to}{\to}F Sing(X)_0

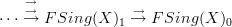
    You want to turn this into a complex by forming the Moore complex of this: the differential is the alterating sum of the maps induced by the boundary maps.

    • CommentRowNumber3.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 23rd 2010
    • (edited Mar 23rd 2010)

    Freaking awesome. That is so cool! You've exceeded my expectations!

    Thank you, I really appreciate it. This is exactly what I was looking for!

    • CommentRowNumber4.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 24th 2010
    The usual description of the complex above is in terms of the alternating sum of the (homomorphisms induced by the) boundary maps, but this is just the Dold-Kan construction in disguise.

    I didn't think that this was the Moore complex, as that involves looking at the intersection of kernels of the induced face maps - it's just the Dold-Kan correspondence. The Moore complex is almost all the way to the cohomology, as you only use one face map, not the alternating sum of all of them.
    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeMar 24th 2010
    • (edited Mar 24th 2010)

    Maybe it is me who uses the terminology incorrectly. See the discussion at Moore complex -- related complexes.

    I don't know. Somehow a word is missing in the standard literature! People like to say "normalized chains complex" when they mean the normalized version. There seems to be no good word for the non-normalized version apart from "the complex". Maybe: "that complex, you know" would be an option.

    • CommentRowNumber6.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 24th 2010
    • (edited Mar 24th 2010)

    "that complex, you know"

    :D

    One could say, 'the Dold-Kan complex associated to a simplicial abelian group', but it is a bit long. I came to the Moore complex via the nonabelian version, so that is where I know it from. In any case, the homology of the Moore complex and "that complex" are isomorphic (naturally so I think), so it is a fine point.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeMar 24th 2010

    By the way, David, you probably accidentally switched your text filter (happens to me every now and then, too). When posting comments, below the edit box choose "Markdown" and then your intended formatting will again appear.

    • CommentRowNumber8.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 24th 2010

    Thanks - I sometimes turn it off so I can do quicker maths comments without using proper LaTeX.

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeMar 24th 2010

    Oh, i see. Never mind me, then. I suspected that you were like me and did this accidentally! ;.)

    • CommentRowNumber10.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 24th 2010

    Yeah, I accidentally forgot to turn them back on!

    • CommentRowNumber11.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 24th 2010
    • (edited Mar 24th 2010)

    Does anybody else find the notion of alternating signs distasteful? (Not to sound too picky), but is there perhaps some sort of "better" structure than imposing strange sign conditions?

    I mean, in the case of, say, deRham cohomology, the signs come from the alternating form, but why should they come up in singular homology?

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeMar 24th 2010
    • (edited Mar 24th 2010)

    One way to think of it is:

    the Dold-Kan correspondence allows us to regard everything related to chain complexes as just a tool and convenient repackaging of the true structure, which are abelian Kan complexes = abelian oo-groupoids.

    From this perspective a chain complex has no further intrinsic meaning and is just a convenient way to encode an abelian oo-groupoids. If it takes alternating signs or whatnot to achieve this, then so be it.

    But of course the signs are not all that arbitrary and pointless. For one, the alternating sum of face maps is precisely the sum of incoming face maps minus the sum of outgoing face maps. So what happens under Dold-Kan is also secretly a step from simplicial shapes to globular shapes. This is more manifest in the non-abelian version of Dold-Kan, which leads not to chain complexes but to crossed complexes. It is also manifest in the beginning of Ross Street's text on orientals.

    • CommentRowNumber13.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 24th 2010

    Incoming face maps and outgoing face maps? I'm not sure that I'm familiar with the terminology, (or I could be missing the point!).

    • CommentRowNumber14.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 24th 2010

    Here's my guess:

    Take a 2-simplex: two of the faces (=edges if you draw it) are source and one is target if you take the simplex (=filler) as a globular shape. For higher simplices there should be a systematic way to say which faces are a component of the source and which are a component of the target. Orientals sounds a good way to do this.

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeMar 24th 2010

    Yes. Look at the pcitures at oriental. An oriental is an "oriented simplex", sort of: is is a simplex thought of as a globular n-category, where each k-morphism has a source and a target (k-1)-morphism.

    You can check that the face maps that appear with a plus-sign in the alternating sum all correspond to source and those with a minus sign all to target, in any given situation.

    • CommentRowNumber16.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 24th 2010
    • (edited Mar 24th 2010)

    The way I draw the 2-simplex, I get one vertex that is a source for two edges, one that is the source for one edge and target of another, and one that is the target for two edges.

    The triangle where all edges are facing rightwards Edit: (Markdown broke my Ascii art)

    Edit: Aren't simplices oriented by definition?

    • CommentRowNumber17.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 24th 2010

    Is it worth reading over Goerss-Jardine for the answer to this, or is it not going to give the moral story?

    • CommentRowNumber18.
    • CommentAuthorUrs
    • CommentTimeMar 24th 2010

    This is not supposed to be a deep point that I am making here.

    For n=2: notice that the two even faces can be composed and the 2-simplex may be regarded as going from the two even faces to the single odd face.

    Similarly for the 3-simplex: the picture given at oriental shows a 3-morphism going from the two even faces to the two odd faces.

    For the 4-simplex, look at that big picture at oriental. The big vertical arrow in the middle goes from the three even faces to the two odd faces.

    For a full formalization of this you can look at Ross Street's The algebra of oriented simplices . But I don't think you want that fully formalized statement.

    • CommentRowNumber19.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 24th 2010

    I couldn't see the picture for some reason! I had to open it in a different browser!

    • CommentRowNumber20.
    • CommentAuthorDavidRoberts
    • CommentTimeMar 24th 2010

    2 simplex = filled triangle, and it is the source and target of the putative 2-arrow that is that filler I was referring to, but Urs has given a better reference.

1 to 20 of 20

  1.