nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
created stub for n-connected object in an (infinity,1)-category
--( made connected redirect to it, so that one can easily link to this entry by saying xyz is 4-connected)
Also added to homotopy group a section on connected and truncated objects.
-
- CommentRowNumber2.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 24th 2010
I would add that an n-connected n-truncated object in an (oo,1)-category is the (oo,1)-categorical version of an Eilenberg-MacLane K(G,n), so it should be equivalent to for some abelian group A.
I'm remarking this since fibraton sequences in Whitehead towers (at least for topologicla spaces) precisely involve this kind of spaces:
and when X=BG, for G some (nice) topolgical group one immediately recovers the classical theory of obstructions for principal G-bundles. For instance, for G=U(N), the whitehead tower begins with
, and one recovers that obstruction to reduce the structure group from to is an element in .
what I find interesting here is that this integral cohomology class is the first Chern class of the -bundle associated to the morphism into . so we can express in terms of the first bit of the whitehead tower of . what I am suspecting now, is that for large (i.e. infinite) N, the whitehead tower of is an incarnation of k-theory spectrum, and that all chern classes will appear this way, as integral classes. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
I'm remarking this since fibraton sequences in Whitehead towers (at least for topologicla spaces) precisely involve this kind of spaces:
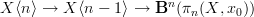
Yes, thanks, good point.
I have typed now what I think is the fully general statement of this at Whitehead tower in an (oo,1)-topos -- Properties
-
- CommentRowNumber4.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 24th 2010
very nice. I added a line in the Examples to say that when X is a pointed topological space, is an Eilenberg-MacLane space. -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
I added a line in the Examples to say that when X is a pointed topological space,
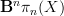 is an Eilenberg-MacLane space.
is an Eilenberg-MacLane space.thanks! I added a further proposition here that asserts that and how this works generally
I will now add more details elsewhere.
By the way, I find the classical article
- Dwyer, Kan, An obstruction theory for diagrams of simplicial sets (pdf)
a good source of classical statements for the kind of statemements that we are after here.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
Domenico,
here a thought on curvatures as obstructions to lifts through Whitehead/Postnikov towers:
classical obstruction theory in Top tells us that to compute iteratively the obstruction to extending a morphism
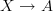 through a morphism
through a morphism 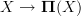 we are to form the Postnikov tower
we are to form the Postnikov tower 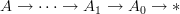 of
of 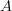 and then lift through that step-by-step, each time picking up the corresponding k-invariant characteristic class as the obstruction.
and then lift through that step-by-step, each time picking up the corresponding k-invariant characteristic class as the obstruction.But this story by itself fails to work sensibly for us in our oo-stack topos
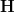 : the k-invariants are not useful here by themselves. For instance if
: the k-invariants are not useful here by themselves. For instance if 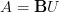 is the coefficient object for complex bundles, the the corresponding (oo,1)-categorical Postnikov tower has essentially just a single term, namely
is the coefficient object for complex bundles, the the corresponding (oo,1)-categorical Postnikov tower has essentially just a single term, namely  itself. That's because
itself. That's because 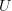 is an ordinary group, so from the point of view of the categorical homotopy groups of
is an ordinary group, so from the point of view of the categorical homotopy groups of 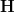 ,
, 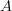 is a 1-type. Of course that just means that it is a Lie 1-groupoid, so it makes sense, but it makes the Postnikov tower non-useful for the obstruction theory.
is a 1-type. Of course that just means that it is a Lie 1-groupoid, so it makes sense, but it makes the Postnikov tower non-useful for the obstruction theory.The thing is that we rather want a Postnikov filtration with respect to the geometric homotopy groups of
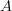 . These are by definition those of
. These are by definition those of 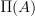 (non-boldface
(non-boldface 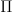 here!). As discussed elsewhere,
here!). As discussed elsewhere, 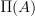 is in fact the geometric realization of the groupoid
is in fact the geometric realization of the groupoid 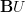 , so
, so 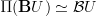 is the correct topological classifying space for the unitary group.
is the correct topological classifying space for the unitary group.We want the Postnikov filtration of
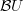 and want to see its real cohomology groups appear as obstructions, which are precisely the Chern classes.
and want to see its real cohomology groups appear as obstructions, which are precisely the Chern classes.So I am thinking: we may have to redo the Postnikov theory of HTT for geometric homotopy groups.
Meaning: we let
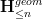 be the full subcategory of
be the full subcategory of 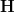 on those objects whose geometric homotopy groups vanish above degree
on those objects whose geometric homotopy groups vanish above degree  . Then we need to check if the inclusion
. Then we need to check if the inclusion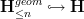 has a left adjoint, the geometric truncation
has a left adjoint, the geometric truncation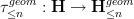
If we could get this, then the rest would go through verbatim as before, but would now produce a Postnikov tower obstruction theory that encodes the desired information. We would decompose
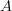 into a geometric Postnikov tower
into a geometric Postnikov tower 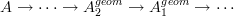 and then lift from
and then lift from 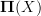 step-by-step through that. In the nth step we should pick up the nth Chern character there (up to issues of how to count :-).
step-by-step through that. In the nth step we should pick up the nth Chern character there (up to issues of how to count :-).I guess that is in principle the right plan. I am just not sure if I am up to the task of finding the required localization left adjoints.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
I guess that is in principle the right plan. I am just not sure if I am up to the task of finding the required localization left adjoints.
On a second thought, it should be clear how it works: we know the localization is specified by the collection of morphisms
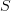 that the left adjoint sends to equivalences. These morphisms in
that the left adjoint sends to equivalences. These morphisms in 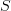 should be those morphisms in
should be those morphisms in 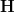 that induce isomorphisms on geometric homotopy groups below degree
that induce isomorphisms on geometric homotopy groups below degree  . Probably.
. Probably. -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
Probably.
Right, so one would have to mimic the proof of HTT, Prop. 5.5.6.18 for another class
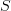 of morphisms than used there. Hm...
of morphisms than used there. Hm... -
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 24th 2010
- (edited May 17th 2010)
We want the Postnikov filtration of and...
precisely. when I was thinking/talking of the Whitehead tower of , that was the tower of as a topological group, so what I was denoting should have correctly been (I tend to mix up these notations when dealing with topological groups, and would have probably used something weird as to denote the delooping of as a group).
so I totally agree with what you write. I'll try to work on the details tomorrow. in the meanwhile, let me point out something I've been using in this last two days informal computations and which I should actually give a proof of (if it is true..). in the -obstructions sequences I've been writing things like: we have fibration sequences
but then I've secretely delooped everything claiming there were fibration sequences
which are the one actually appearing in the obstruction theory for -bundles.
so I should justify this delooping of fibration sequences I implicitly used. I guess it should be easy to state and prove, but now it's too late even for this, I'll think to this tomorrow morning. -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
I think actually the "delooped" sequences are the fundamental ones. The other ones are "looped" :-)
In applications it's the "delooped" sequences that matter for the obstruction theory, as you say, and whose homotopy fibers we are actually interested in
By the way, discussion along these lines that you indicate is for instance at string structure and related entries.
-
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 25th 2010
I think both looped and delooped sequences are interesting here: it is something saying "if X is deloopable, then its Whitehead tower is deloopable", which in a single sentence says that given a (nice) topological group G, the connected component of the identity and the universal cover of G are groups, and also all higher covers of G (at least, up to homotopy). this should be straightforward (but let me think to the details..) -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Yes, right, both are interesting I think what I mean is that we start with a coefficient object
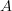 and are interested in its decompositions. In applications that
and are interested in its decompositions. In applications that  is
is
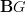 and not
and not 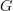
I think in Top, whatever statement about Whitehead towers of an object
 one has, they will induce corresponding statements about the Whitehead towers of the looping of
one has, they will induce corresponding statements about the Whitehead towers of the looping of 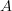 . That's because the construction of Whitehead towers as well as that of the looping involves only (homotopy) limits which hence commute with each other, and the coskeleton functor which is right adjoint and hence also commutes with them.
. That's because the construction of Whitehead towers as well as that of the looping involves only (homotopy) limits which hence commute with each other, and the coskeleton functor which is right adjoint and hence also commutes with them.In a general oo-topos I need to think about how to adapt this statement, as there everything is the same except that at one point we apply
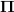 , which is left adjoint.
, which is left adjoint.Hm...
-
- CommentRowNumber13.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 25th 2010
it seems I'm completely tired and unable to do anything, today.. :(
anyway, what I was thinking is that, since the point (the terminal object) is deloopable, we should have a good notion of deloopable morphism, and as a particular case an object X should be deloopable when the terminal morphism is deloopable. I'm saying this cause at delooping there's a characterization of deloopable objects, but a notion of deloopable morphism seems to be lacking. -
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
a notion of deloopable morphism seems to be lacking.
Typically we would pass to the over-oo-category over a given object and call the looping/delooping on objects there the looping/delooping of the corresponding morphisms.
Do you have concretely an example in mind where you want to be delooping a morphism?
-
- CommentRowNumber15.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 25th 2010
that was my first idea, too: relative deloopable objects. but that did not correspond to what I had in mind, which is characterizing the image of the free loop space functor: given a morphism in, say, Top, when is it of the form ? the main example I'm aiming at is the Whitehead tower of for a nice topological group (there must be a simple explanation of the fact that higher covers of a topological group admit a topological group structure and/or an higher topological group structure, and that the involved fibrations are group homomorphisms, but this simple abstract nonsense explanation is still escaping me) -
- CommentRowNumber16.
- CommentAuthorDavidRoberts
- CommentTimeMar 25th 2010
Well for a topological group the fundamental n-groupoid is internal to groups, and so is deloopable (for n=1 this is due to Brown-Higgins, and for n=2 I wrote it down somewhere, but it is fairly obvious). Then the homotopy fibre over the identity element (=trivial group) regarded as an object of Pi_n is also internal to groups. That one can calculate this as the ordinary pullback of the tangent category (which is again internal to groups) shows that this construction works internally. As the whole thing is done internal to groups, we can deloop the n-connected cover of G to an n+1 connected cover of the delooping of G -
- CommentRowNumber17.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
thanks. let me see if I understand this correctly. if is a nice topological space (in aprticular it should be locally enough-connected) then is a topological n-groupoid, and the constant-paths inclusion is a morphism of topological n-groupoids. taking the (homotopy) fiber of gives a toplogical n-groupoid with a morphism to . now, since the homotopy fiber is the product of two topological 0-groupoids over a topological n-groupoid, it is a toplogical 0-groupoid (is this correct). so is just a (or better, is equivalent to a) morphism of topological spaces, and it is the (n+1)-connected cover of .
when is a topological group, the construction is internal to groups (this essentially because maps froma a simplex to a group are naturally a group with pointwise multiplication) so one ends up with a morphism of topological groups . -
- CommentRowNumber18.
- CommentAuthorDavidRoberts
- CommentTimeMar 26th 2010
Ah, not quite. The homotopy fibre is one categorical dimension lower than Pi_n, namely n-1. Thus the 1-connected cover is a space (=topological 0-groupoid), the 2-connected cover is a topological 1-groupoid (as in my thesis) and so on (hypothetically and ideally using Trimble groupoids for choice, or Kan complexes if you are so inclined and seem to indicate above). The n-connected cover should be a topological (n-1)-groupoid. But as you say, the construction works internal to topological groups. Then the geometric realisation of this (n-1)-groupoid internal to topological groups should be a topological group. -
- CommentRowNumber19.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 26th 2010
I see and actually had thought to the (n-1)-categorical dimension, but then I got confused about the 0th step: taking the connected component of a point (e.g., of the identity in a topological group). from the categorical abstract nonsense that seems to be a topological (-1)-groupoid, but I would have expected it to be a honest topological space (i.e., topological 0-groupoid). so I tried to think to what exactly happens for the homotopy fiber of and of . In the first case it seems to em taht one obtains what a priori is a topological 1-groupoid, but looking at morphisms, one sees that hom-spaces are trivial, so this is actually a topological 0-groupoid. for I'm not confident in my ability of explicitly describing a homotopy fiber, but I had come to the conclusion that not only 2-hom spaces were trivial, so that one has a topological 1-groupoid, but also 1-hom spaces were contractible, so that one could in some sense think of this 1-groupoid as a 0-groupoid (but I cannot say I am confident in this argument) -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
so that one has a topological 1-groupoid, but also 1-hom spaces were contractible, so that one could in some sense think of this 1-groupoid as a 0-groupoid (but I cannot say I am confident in this argument)
Suppose the pointed space X is already connected and simply connected and compute the homotopy fiber of
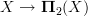 . This is the ordinary pullback of the "tangent 2-groupoid" of
. This is the ordinary pullback of the "tangent 2-groupoid" of 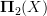 : objects are paths in X from the basepoint. Morphisms are homotopy classes of fillings of triangles of paths, and 2-morphisms are "paper cup" diagrams of such fillings.
: objects are paths in X from the basepoint. Morphisms are homotopy classes of fillings of triangles of paths, and 2-morphisms are "paper cup" diagrams of such fillings.Pulling this back to X gives you the bundle of topological groupoids which over each point x in X has: objects the path from the basepoint to X, morphsism the homotopy classes of surfaces between these paths. This is equivalent to
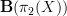 .
. -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
... which is just the special case of the formula that we derived at Whitehead tower in an (infinity,1)-topos: the topological groupoid
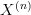 sits in a fibration sequence
sits in a fibration sequence 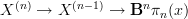 , hence is a
, hence is a 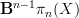 - bundle over
- bundle over 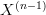 .
.The ordinary higher covering space (as a topological space) that you expect to see is the geometric realization of this.
-
- CommentRowNumber23.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 26th 2010
I finally see it! and so what makes the difference between the topological and the Lie case is that in the latter there is (above first step) no "Lie realization". so the Whitehead tower of a Lie group is really made of n-Lie groups. however, one has a partial Lie realization: , so that using as a realization of , one gains one categorical degree in the Lie framework. so, for intance, the 3-connected cover String(n) is a topological group or a Lie 2-group, and the 7-connected cover Fivebrane(n) is a topological group or a Lie 6-group.
(in case this should happen to be correct, please, be extremely cautious in telling me so: I could stand up, run to the window and cry I see the light! :-) ) -
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
I finally see it! and so what makes the difference between the topological and the Lie case is that in the latter there is (above first step) no "Lie realization". so the Whitehead tower of a Lie group is really made of n-Lie groups. however,
Yes! The internal Whitehead tower, internal to the Lie oo-topos. Yes. It also has an underlying topological tower, tough, in Top. Under the non-boldface
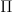 .
.however, one has a partial Lie realization:
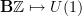 ,
,Yes. I would put it like this: if we want to refine ordinary cohomology in Top and the extensions it classifies to the Lie context, then it matters for the smooth structure whether we use
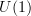 or
or 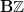 .
.for intance, the 3-connected cover String(n) is a topological group or a Lie 2-group, and the 7-connected cover Fivebrane(n) is a topological group or a Lie 6-group.
Yes!
(in case this should happen to be correct, please, be extremely cautious in telling me so: I could stand up, run to the window and cry I see the light! :-) )
Oops, i wasn't being cautious... :--)
-
- CommentRowNumber25.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 26th 2010
I SEEEE THE LIGHTTTTTTT!!!!!!!!!!! -
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
All right!
So let's put some of this light into the entry.
I started polishing the Examples-section at Whitehead tower in an (infinity,1)-topos a bit
I moved the discussion of Postnikov towers by coskeletons and the Duskin reference to Postnikov tower in an (infinity,1)-category
I expanded on the remarks involving the use of the decalage construction to compute the homotopy pullback that defines the Whitehead tower elements in sSet.
David Roberts should have a look if he agrees with what I did so far.
-
- CommentRowNumber27.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 26th 2010
the light is suggesting me the following remark: let be a Lie group and let be its higher covers, as higher Lie groups. now consider the Lie algebra of . then does not know about , but it dies know about ! but then it knows about all the higher covers of , and so about their higher Lie algebras! so, for instance knows .
well known, I know, but I clearly see it only now.
next thought: is there a representation theory for higher Lie groups (taking values in higher vector spaces)? is there an higher equivariant version of extended topological quantum field theory?
time to sleep.. -
- CommentRowNumber28.
- CommentAuthorDavidRoberts
- CommentTimeMar 27th 2010
@Domenico
I got confused about the 0th step: taking the connected component of a point (e.g., of the identity in a topological group). from the categorical abstract nonsense that seems to be a topological (-1)-groupoid, but I would have expected it to be a honest topological space
I was trying to think about this step in the context of the classical Whitehead construction recently and I got confused in a different way. But giving it another go, I came up with this: The zeroth stage
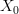 in the Postnikov tower of
in the Postnikov tower of  (as constructed using topological n-groupoids) should be the Cech groupoid of the map
(as constructed using topological n-groupoids) should be the Cech groupoid of the map 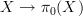 (a unique arrow between any two points in a path component - we assume that
(a unique arrow between any two points in a path component - we assume that  is locally well-behaved for components and path-components to be the same ). Thus this is a topological groupoid which is equivalent (internally!) to a set, the 0-type of
is locally well-behaved for components and path-components to be the same ). Thus this is a topological groupoid which is equivalent (internally!) to a set, the 0-type of  . Then, as usual,
. Then, as usual,  is pointed so that
is pointed so that 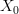 is a pointed groupoid. To construct the homotopy fibre we can take the source fibre of
is a pointed groupoid. To construct the homotopy fibre we can take the source fibre of 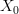 over the basepoint (this is just a shortcut description of the usual tangent category construction), which is a space over
over the basepoint (this is just a shortcut description of the usual tangent category construction), which is a space over  by the restriction of the target map. This space is precisely the connected component of the basepoint of
by the restriction of the target map. This space is precisely the connected component of the basepoint of  , if I am not mistaken.
, if I am not mistaken. -
- CommentRowNumber29.
- CommentAuthorDavidRoberts
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
Looks good, Urs.
One thing I would like to edit, but the spam filter is blocking me, is in the section construction using topological groupoids, where I say
As the space is locally contracible, in particular semi-locally
 -connected, the space
-connected, the space 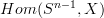 is semi-locally simply-connected (I have a fragment of a paper saying this is true for the 'absolute case' - that is, locally
is semi-locally simply-connected (I have a fragment of a paper saying this is true for the 'absolute case' - that is, locally  -connected implies the mapping space locally simply connected, but I expect it to be true for the relative case -DMR)
-connected implies the mapping space locally simply connected, but I expect it to be true for the relative case -DMR)This is essentially now Corollary 5.9 in my thesis, but taking the space of pointed maps instead of all maps. The proof (a new one, not from the paper mention) is given in detail.
-
- CommentRowNumber30.
- CommentAuthorDavidRoberts
- CommentTimeMar 27th 2010
Domenico
I think I have it - the construction for the 0-connected cover gives a (-1)-groupoid ... over X. Thus it is really a bundle of (-1)-groupoids, i.e. a sub-'set'. More generally, the n-connected cover is an (n-1)-groupoid over X (parameterised by X, internal to things over X, and so on), and so has categorical dimension max{1,n-1}.
I am reminded of Grothendieck's thoughts in the early parts of Pursuring Stacks, where he says the most general n-groupoids will be parameterised by some site i.e. bundles/stacks of groupoids. -
- CommentRowNumber31.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
over X, yes! the fibre over a point is TRUE if we get that point, or FALSE if we don't get it. that's it.
now I think we should stress this bundle-perspective:
first, a 0-groupoid is not a set: it is a set with a relation (hom(x,y) is a truth value);
second, the bundle -bundle is the flat higher-bundle given by the natural representation given by . -
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
Concerning the bundles of (-1)-groupoids: yes, exactly: bundles whose fiber either is a point or empty.
David wrote:
I am reminded of Grothendieck's thoughts in the early parts of Pursuring Stacks, where he says the most general n-groupoids will be parameterised by some site i.e. bundles/stacks of groupoids.
Sure, we start with oo-groupoids parameterized by all topological spaces, these are topological oo-groupoids. Then if you have a particular one over a topological space, you can pull back from that gros site to the petit site of that space, to get one parameterized by that space.
This is a general principle: for C a category of test spaces,
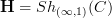 is the gros topos of all oo-groupoids modeled on them. Given any object
is the gros topos of all oo-groupoids modeled on them. Given any object 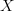 in there, the overcategory
in there, the overcategory 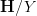 is the "petit oo-topos" of
is the "petit oo-topos" of 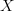 .
.Domenico wrote:
second, the bundle
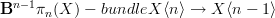 is the flat higher-bundle given by the natural representation
is the flat higher-bundle given by the natural representation 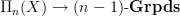 given by
given by 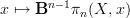 .
.Let me seee: that looks sensible, but can you see this formally? From that diagram in the proof at Whitehead tower in an (infinity,1)-topos we kow that the bundle
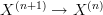 is classified by the map
is classified by the map 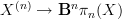 which is the pullback of
which is the pullback of 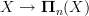 along
along 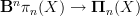 .
.Now I'd need to use
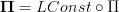 and the adjunction
and the adjunction 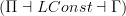 to manipulate this to get it into the form you mentioned. Ahm, I can almost see this. But not quite actually. Hm..
to manipulate this to get it into the form you mentioned. Ahm, I can almost see this. But not quite actually. Hm.. -
- CommentRowNumber33.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 27th 2010
indeed, the description of the morphism I suggested above is not quite correct. for , for instance, one would get , but since the set on the right is pointed this would give a section, and so the universal cover of would be trivial. the right fiber is (obviously, now that I write it) , where is the chosen basepoint. -
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeMar 27th 2010
Yes, that looks right.
-
- CommentRowNumber35.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 27th 2010
so the construction is in some sense tautological: a point in which most of (all?) the possible definitions of higher category agree is that an n-category is enriched over (n-1)-categories. so once a 0-object is fixed, each n-category is naturally a bundle of (n-1)-categories over 0-objects. and in considering the homotopy fibre of constant path inclusion it seems we are precisely realizing this bundle. -
- CommentRowNumber36.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 27th 2010
@David, @Urs:
it's holiday time in Italy, I'll be away for a while. back on the Lab on April 5th. -
- CommentRowNumber37.
- CommentAuthorDavidRoberts
- CommentTimeMar 28th 2010
Cheers, Domenico, have fun. -
- CommentRowNumber38.
- CommentAuthorUrs
- CommentTimeMay 27th 2010
added a liitle bit more details to n-connected object of an (infinity,1)-topos
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeDec 21st 2011
- (edited Dec 21st 2011)
At n-connected object of an (infinity,1)-topos I have
added the recursive characterization of n-connected morphisms;
added an Examples section “In Grpd” where I state the fact that 0-connected morphisms between groupoids are precisely the eso+full functors, and then spell out the proof.
(Probably there is a quicker proof using something or other. I just check it explicity.)
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeDec 21st 2011
- (edited Dec 21st 2011)
Probably there is a quicker proof
Of course in ∞Grpd one can check connectedness of morphisms by checking connectedness of homotopy fibers over each connected component. It is immediate that an eso+full functor of groupoids has connected (homotopy) fibers.
But that argument does not seem to generalize well to stacks, unless I am missing something. I believe the argument that I wrote up does:
A morphism between two groupoid-valued presheaves that is objectwise an eso+full functor is a 0-connected morphism of stacks.
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeMar 12th 2012
- (edited Mar 12th 2012)
I felt like making explicit in this subsection that in a hypercomplete ∞-topos the notions of n-connected / n-truncated form not just a linear hierarchy, but a “clock”, which wraps around at
- ∞-truncated = any morphism = (-2)-connected
and at
- ∞-connected = equivalence = (-2)-truncated -
1 to 41 of 41