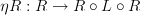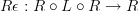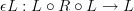nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
I asked a question at adjunction.
Edit: Also created experimental alternative definition of adjunction
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
Check it yourself. It is a useful exercise.
-
- CommentRowNumber3.
- CommentAuthorEric
- CommentTimeMar 25th 2010
I did check it :) That is why I'm asking, to make sure my check was correct. I should say more accurately, I didn't "check it", I derived it and want to know if I made a mistake.
-
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Oops! Typo. My bottom arrow should go right to left. I transcribed it wrong. Will fix it now.
-
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Argh. The arrows should also go up not down. Tragedy of poor cut and past. Will fix it
Edit: I fixed the typos at adjunction, but Toby is editting experimental alternative definition of adjunction :o
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
Please check it yourself and also do not put it at the top of the page, if you have to put it there at all.
-
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Now that I created experimental alternative definition of adjunction, I removed the question from adjunction.
-
- CommentRowNumber8.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
You should probably have named that incorrect definition of an adjunction, although I haven't checked.
Basically, either your "definition" is just one of the other definitions restated in a more abstruse way, or it's incorrect.
-
- CommentRowNumber9.
- CommentAuthorEric
- CommentTimeMar 25th 2010
@Harry: You have the potential to be helpful. From your comment, it is obvious you haven't even read it (or Toby's response). Do you really think that was necessary or even appropriate?
-
- CommentRowNumber10.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Yes, I do. I think that you should try to prove it. That is, if you're going to try to come up with an alternative definition, attempt a proof first. Then put up your proof with your question. Something like "does this work", etc.
Here's the problem. You can make up definitions faster than anyone here can answer your questions. It's like, "is this an equivalent definition?" "I have no idea. I can check the same way that you can check."
If you never even try to prove it, you won't learn how to prove things like that, and then you'll keep asking questions like that. I think that the stance to take here is to encourage you to try. As you can see in the other thread, you were completely and totally mistaken about what functoriality means. I'll let the other people involved give their takes on it, but I found it a little bit silly that I was sitting there giving you the definition of a functor multiple times, but my words fell on deaf ears.
Anyway, as it stands, that definition is wrong. Even if you fix it, it's going to be more complicated than:
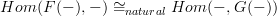
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Here is the story...
I am trying to understand adjunctions, so I look at the nLab [gulp!] No chance of me understanding that. I check out MacLane. Nope. I like MacLane's book, but it is not written in a style I can easily absorb. So I pick up Goldblatt.
Low and behold. There is a picture that looks eerily similar to what I drew at experimental alternative definition of functor, but with things slightly rearranged. So I combined my diagram with his (any complaints about my diagram should apply equally to his so I'm not too worried about that) and after connecting a few "2-cells" ended up with that commuting square.
Since I derived it, that counts as a "check" based on the best of my knowledge. Since I derived it in an attempt to understand adjunctions, then I thought someone who understands adjunctions could look at the diagram and tell me if it is correct. Toby had some encouraging words, but the jury is still out.
If this diagram is correct, it means I understand adjunctions. If not, I have some work to do. If I were bet on it, I'd bet I have some work to do.
Edit: If it is correct, this is great news for "scientists and engineers" because I'm sure they can understand this much better than other (hopefully equivalent) definitions.
-
- CommentRowNumber12.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Come on..
Just think about it.
The definition I just cited is the easiest way to define what is going on.
-
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Maybe for a math student. I think I represent a large portion of the non-math population, i.e. "scientists and engineers" and I assure you mine (if correct) would be much easier for them to understand than yours.
-
- CommentRowNumber14.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
I disagree. My statement is a statement about a bijection of sets. Your statement involves commutative diagrams.
-
- CommentRowNumber15.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Since you are neither a scientist nor an engineer, you do not have a say in what they find easier ;)
-
- CommentRowNumber16.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
I think that you're doing it wrong.™
I'm done arguing with you about this. The problem is not with category theory...
-
- CommentRowNumber17.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Category theory is beauty. I never said it was wrong and I never said it had any problems. The fact I do not find some definitions "optimal" is my problem, not category theory's. Rather than sit back and complain, I'm trying to do something about it. If I can find (equivalent, but simpler) definitions I'm happy with, maybe, just maybe, it might help others like me who are trying to learn.
-
- CommentRowNumber18.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Update: The experimental alternative definition of adjunction is taking better shape now. There are even some equations we can check. Now I just need to try to decipher the standard definition well enough so I can write down similar equations using the standard definition. OR massage these equations into something looking more like the standard definition.
Believe me, I'm trying to check this myself...
-
- CommentRowNumber19.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
It is not equivalent based on a quick check.
At least to the extent that it is well-defined.
Eric, it appears that you're having trouble with these definitions. Have you tried those catsters videos?
-
- CommentRowNumber20.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Thanks Harry. Yeah, the Catster videos are great. I'm the one that put think link to them on adjunction. I'll need to watch it again now that I'm giving this a second shot. Watching the video the first time fooled me into believing I understood it (good teachers can do that!), which obviously isn't the case.
-
- CommentRowNumber21.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
I've never actually watched them, but I've heard good things.
-
- CommentRowNumber22.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Edit: I asked an(other) embarrassing question and removed it.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
The diagram you draw almost (up to reversal of some arrows and renaming of some variables) lloks like a diagram that encodes part of the fact that the counit of an adjunciton is natural.
But I'd really rather go the other way. If the standard definition of adjunction looks complicated, that's an illusion of notation. Let's look at the standard definition first, and see what it means. After you understand it, you can entertain yourself with finding equivalent definitions.
Back in the other thread we talked about one example of an adjunction and went through seeing that it is an adjunction in great detail. Do you understand what we did there? I'd feel it would be better if you replied to the discussion we had there than throwing another guess at an alternative definition at us. Usually the idea is that one starts trying to redo something after one has understood it.
The standard definition of adjunction says that a functor
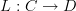 is left adjoint to a functor
is left adjoint to a functor 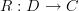 precisely if for all objects
precisely if for all objects  and
and  we have that morphisms
we have that morphisms 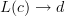 in
in  can naturally be identified with morphisms
can naturally be identified with morphisms 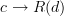 in
in  .
.This is simple, isn't it? Which part of it looks not understandable?
I don't want to discuss any more alternative definitions. I would like to see you understand the standard definitions of category, functor, natural transformation and adjunction. It's easy. There is no mystery here. It is elementary, you just manipulate some sets of things.
-
- CommentRowNumber24.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Usually the idea is that one starts trying to redo something after one has understood it.
You should know by now I am not "usual" (for better or worse).
I would be your worst nightmare as a student. I simply cannot learn something by reading standard definitions. I do literally need to "find my own way". I have no choice about it.
But to your point, I agree. I am turning attention back to the standard definition now that I made some progress "my own way". For example, I now know the second diagram, the one I incorrectly attributed to it being an endofunctor, is actually due to the natural transformation
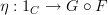 .
.The first diagram there does not commute, hence the Crash!...
I hope to first understand what a adjunction is and then return to your simple example. I know you would have me do it the other way...
-
- CommentRowNumber25.
- CommentAuthorEric
- CommentTimeMar 25th 2010
PS:
The standard definition of adjunction says that a functor
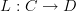 is left adjoint to a functor
is left adjoint to a functor 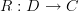 precisely if for all objects
precisely if for all objects 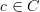 and
and 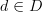 we have that morphisms
we have that morphisms 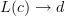 in
in  can naturally be identified with morphisms
can naturally be identified with morphisms 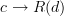 in
in  .
.By the way, I think this is what Goldblatt's diagram was trying to say, but I took visual "naturally identified" the wrong way. What does it mean for two morphisms to be naturally identified?
-
- CommentRowNumber26.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Edit: Argh. Another embarrassing question.
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Usually the idea is that one starts trying to redo something after one has understood it.
You should know by now I am not "usual" (for better or worse).
Okay, but here I am getting the impression that we are not making progress with the unusual way. The definitions we are talking about are elementary, and should be gotten under control.
The standard definition of adjunction says that a functor L: C \to D is left adjoint to a functor R: D \to C precisely if for all objects c \in C and d \in D we have that morphisms L(c) \to d in D can naturally be identified with morphisms c\to R(d) in C.
By the way, I think this is what Goldblatt's diagram was trying to say,
If he gives a definition of adjunction, this must be what he was trying to say. But can you see it? Do you understand the above definition? If not, what about the above sentence is not clear to you?
-
- CommentRowNumber28.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Do you understand the above definition? If not, what about the above sentence is not clear to you?
No. I don't know what it means for two morphisms to be "naturally identified".
I've been staring at adjunction literally for hours now. I still do not know what
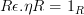 means :( The diagram looks like total chaos to me.
means :( The diagram looks like total chaos to me. -
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
No. I don't know what it means for two morphisms to be "naturally identified".
Okay, then you should ask. We already talked about this quite a bit in the other thread.
It means two things:
the set of all morphisms of the form
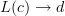 in
in  is in bijection with the set of all morphisms of the form
is in bijection with the set of all morphisms of the form 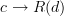 in
in 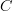 : you can match them one-to-one
: you can match them one-to-oneand one can find one such bijection
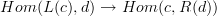 that is "compatible with composition" of morphisms.
that is "compatible with composition" of morphisms.
Don't worry about the second part for the moment. Let's concentrate on the first part, first. This is the defining characteristic of an adjunction, that we have bijections of sets
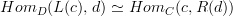
Do you understand this notation? It means just what I said before in words.
This is all there is to the definition of adjunctions. No mystery. Just this.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Eric, I have to run now and take care of some other things for a while.
For the future, I would like to ask if we could proceed this way, for a while: no more experimental wild guesses for a while, until you have a first idea of what's going on. Instead, ask questions about what our replies mean again and again until you understand all the words.
What we just said is what Harry and I have said many times before already in this discussion. I didn't know that it wasn't clear.
While he is not being polite, Harry's technical answers here in this discussion are quite correct. He understands functors, natural transformations and adjunctions. I think if you try to get into a genuine question-and-answer mode with him, that could cause progress.
-
- CommentRowNumber31.
- CommentAuthorEric
- CommentTimeMar 25th 2010
Thanks Urs. I'm at home now and I plan not to sleep until I get this. Until now I was at work and, although I tried, I could not fully concentrate. I have Goldblatt and MacLane and all your and Harry's comments. I will sit down with paper and pencil and figure this out once and for all.
Thank you both for doing your best to help me. I know it isn't easy.
-
- CommentRowNumber32.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
LIGHT BULB!!!
After many many sheets of drawings and reading Goldblatt over and over again, I FINALLY made some progress after watching the Catsters video.
One reason I was confused was because I didn't know what
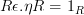
and
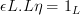
meant. I looked at that and thought "How do you compose a functor with a natural transformation?????"
Now I understand this is a kind of notational convenience. You're not really composing a functor and natural transformation. Since
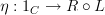
and
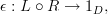
then
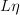 is kind of like a "push forward" in differential geometry. It means the natural transformation
is kind of like a "push forward" in differential geometry. It means the natural transformation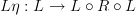 .
.With an adjunction, we get 4 such natural transformations
This is obvious for the experts, but might be worth writing down on adjunction just to be clear what is meant.
-
- CommentRowNumber33.
- CommentAuthorEric
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Edit: Removed question about string diagrams. I get it now.
-
- CommentRowNumber34.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
See, as soon as you stopped trying to come up with your own definitions, this became a lot easier for you.
-
- CommentRowNumber35.
- CommentAuthorFinnLawler
- CommentTimeMar 25th 2010
@Harry: I don't think there's any need to be quite so curt with Eric. I suspect that, if he's anything like me, his insight came at least partially as a result of his other attempts to understand this, not in spite of them.
I personally certainly find that understanding a piece of maths is a matter of finding the right conceptual perspective, and that finding it usually involves unsuccessfully trying several others. But these failures themselves often lead to increased understanding of the other ways of looking at the problem, so non-standard approaches like Eric's, even if eventually unsuccessful, are not to be discouraged.
Just my two penn'orth.
-
- CommentRowNumber36.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
You do not have any context on the matter. This is a repeat of something that happened earlier this week.
-
- CommentRowNumber37.
- CommentAuthorFinnLawler
- CommentTimeMar 25th 2010
I'm not trying to start an argument, Harry. All I mean is that patience is a virtue, especially when it comes to understanding category theory.
-
- CommentRowNumber38.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Finn Lawler, in category theory, a lot of the work in understanding general ideas like this comes from trying to abstract the ideas from concrete examples and then trying to come up with your own definitions. You need to have cases that you understand and then try to formulate a general idea that encompasses all of them. What Eric was doing was coming up with arbitrary definitions not based on anything concrete.
If you go back to the other thread, you'll see why I was short with Eric earlier in the thread. This was essentially something we had just talked about, and Eric was not listening to what Urs or I had to say.
-
- CommentRowNumber39.
- CommentAuthorFinnLawler
- CommentTimeMar 25th 2010
OK, I understand your being annoyed if you felt that you hadn't been listened to. But when you say
You need to have cases that you understand and then try to formulate a general idea that encompasses all of them.
I think you're missing my original point. This may be a common way of coming to understand things, but it's by no means universal. And our own idiosyncratic ways of learning seem to us so natural and obvious that when two conflict we can end up talking at cross purposes and getting quite frustrated.
Anyway, this isn't really the place for a long discussion on that topic. I'm sorry if my comment came off as high-handed, but this is an issue close to my heart.
Maybe what we all should do is wait for Eric to make some more progress on his own and report back.
-
- CommentRowNumber40.
- CommentAuthorEric
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Yep yep. Finn Lawler hit it on the head. Thanks for that. I had seen the definition. I had seen the Catsters video. I had read Goldblatt. I had read MacLane. I had read nLab. I had read Urs' and Harry's comments. I wasn't ignoring you. But the only thing that got me make real progress was to draw pages and pages of pictures. These pictures do not appear in any of the mentioned resources. I even described above that this is the way I must learn. I don't expect anyone to understand it and to be honest, I don't really care. I'm quite happy with where my ways have taken me.
By the way, the diagram on the nLab is horrible. The nLab page should at least contain the words, "Given functors
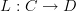 and
and 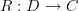 , an adjunction consists of two natural transformations
, an adjunction consists of two natural transformations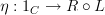
and
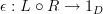
such that
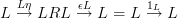
and
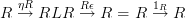 ."
."At least I now understand the words of the definition, but I need to play with it a little, e.g. re-examine the free category example, before I will understand enough to use it.
-
- CommentRowNumber41.
- CommentAuthorEric
- CommentTimeMar 26th 2010
PS: If what I wrote is correct above, I can add it to adjunction.
PPS: Even if Harry was a little curt, it is fine. I really appreciate the fact he was here at all trying to help me. Even despite me being so dense.
-
- CommentRowNumber42.
- CommentAuthorHarry Gindi
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
The wikipedia page on adjoint functors is significantly better than the nLab page, by the way.
It's probably one of the best math-related articles on the whole site.
-
- CommentRowNumber43.
- CommentAuthorEric
- CommentTimeMar 26th 2010
I've changed
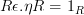
and
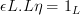
to
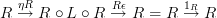
and
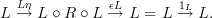
I also added a link to Wikipedia. As a tribute to all the help here, I will try to gather what I can and improve adjunction.
-
- CommentRowNumber44.
- CommentAuthorEric
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Hmm...
I just noticed Toby changed
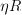 and similar to actual compositions such as
and similar to actual compositions such as 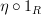 and similar. Now I'm confused again...
and similar. Now I'm confused again...We have
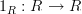
and
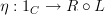
so how can you compose them?
Given a natural transformation
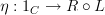 and a functor
and a functor 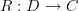 , then I'm 95% sure without even doing any calculations that we can show this "pulls back" to a natural transformation
, then I'm 95% sure without even doing any calculations that we can show this "pulls back" to a natural transformation 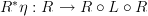 via "pre-composing
via "pre-composing 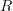 on the right" and I convinced myself that
on the right" and I convinced myself that 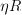 was simply notation for this process.
was simply notation for this process.Similarly, given a functor
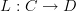 we can "push forward"
we can "push forward" 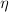 by post-composing on the left, i.e.
by post-composing on the left, i.e. 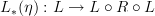 , which I convinced myself is what is meant when people write
, which I convinced myself is what is meant when people write 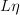 .
.Have I gone astray?
-
- CommentRowNumber45.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
how can you compose them?
You compose
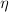 with
with 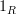 using horizontal composition. Sorry that I haven't gotten around to using the new SVG editor, but try this picture from codecogs (or even edit the picture). You should be able to see that the final composite goes from
using horizontal composition. Sorry that I haven't gotten around to using the new SVG editor, but try this picture from codecogs (or even edit the picture). You should be able to see that the final composite goes from 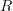 (or
(or 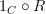 , but that's the same as
, but that's the same as 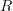 ) to
) to 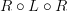 ).
).I put those circles and things in there because it seemed to me to make things more explicit, which is what you seemed to be doing. Note also that horizontal composition is different from vertical composition, which is the kind of composition that was denoted by
 (rather than
(rather than  ) before you started to edit the page.
) before you started to edit the page.When thought of as an operation between
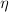 and
and 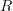 (rather than as an operation between
(rather than as an operation between 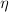 and
and 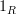 , this is also called whiskering (on the left). You can read about that on strict 2-category; in the notation that I used on that page, this would be written
, this is also called whiskering (on the left). You can read about that on strict 2-category; in the notation that I used on that page, this would be written 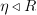 . But that's not very widely used notation, so I wrote things in terms of horizontal composition with
. But that's not very widely used notation, so I wrote things in terms of horizontal composition with 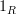 instead of whiskering with
instead of whiskering with 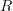 , since the notation for horizontal composition is more fixed.
, since the notation for horizontal composition is more fixed.I don't think that anybody writes this as
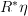 or
or 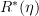 , although I can see why you might want to write it that way. (It was written simply
, although I can see why you might want to write it that way. (It was written simply 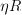 before I edited the page, of course.) Sometimes people will also write
before I edited the page, of course.) Sometimes people will also write 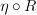 , conflating whiskering with horizontal composition (or conflating
, conflating whiskering with horizontal composition (or conflating 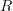 with
with 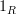 ).
). -
- CommentRowNumber46.
- CommentAuthorEric
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Interesting! Thank you Toby. I'll have to think about it....
PS: On the Catsters video, they also write
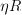 .
. -
- CommentRowNumber47.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
So the short version of my last comment is this:
The operation that you interpreted as being something like pull-back is called whiskering. (Well, whiskering on the left. And the push-forward thing is whiskering on the right.) Since you were making the notation more explicit, I thought that I would do the same for the whiskering. And since there isn't really one standard notation for whiskering, I wrote it as horizontal composition with an identity transformation, which comes to the same thing.
In any case, if you understood what
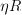 meant, that's the same thing as what
meant, that's the same thing as what 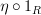 means.
means. -
- CommentRowNumber48.
- CommentAuthorFinnLawler
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Edit: Toby beat me to it, but here's my contribution anyway.
No, that's right. Here
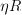 is short for
is short for 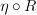 , the horizontal composite or "whiskering". This is different from vertical composition of transformations between functors with the same source and target.
, the horizontal composite or "whiskering". This is different from vertical composition of transformations between functors with the same source and target.If you have
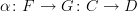 and
and 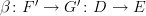 , then the horizontal composite
, then the horizontal composite 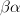 goes from
goes from 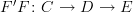 to
to 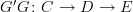 -- that is, the boundary of the composite is the composite of the boundaries. So thinking of
-- that is, the boundary of the composite is the composite of the boundaries. So thinking of 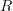 as the identity transformation
as the identity transformation 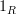 , you have
, you have 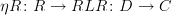 .
.Pictures really help here, I find. I'd write more, but I'm in a rush. Keep trying! It'll all make sense in the end.
-
- CommentRowNumber49.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
Each equation at adjunction is written two ways, originally one way (on the left) very concise and like a formula and then another way (on the right) very spread out and like a diagram. You (Eric) changed the way on the left into something a little more spread out and like a diagram but still more concise and like a formula than the way on the right. I decided to restore the original consise and formula-like way, but not get rid of your new way, making three ways in all to write each of the two equations.
Hopefully, this helps you see a sort of progression of symbolism from something concise and formulaic into something spread out and diagramatic. (Although the far right could stand to be spread out even a little bit more, maybe.)
This is not to say that you can't continue to concentrate on the middle of each.
-
- CommentRowNumber50.
- CommentAuthorHarry Gindi
- CommentTimeMar 26th 2010
Can we always whisker? If we can, does this make Cat a double category?
-
- CommentRowNumber51.
- CommentAuthorEric
- CommentTimeMar 26th 2010
Yep yep. Thanks Toby. That is great. More to think about...
Thanks Finn. One reason I love category theory is the pictures, so now I'll need to learn about horizontal and vertical composition through more drawings :)
-
- CommentRowNumber52.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
@ Harry #50:
I don't know any way that
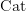 is a double category, except the two degenerate ways in which any 2-category may be interpreted as a double category.
is a double category, except the two degenerate ways in which any 2-category may be interpreted as a double category.Whiskering on the left can be done in this situation: an object
 , an object
, an object  , an object
, an object  , a morphism
, a morphism  , a morphism
, a morphism 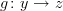 , a morphism
, a morphism 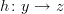 , and a 2-morphism
, and a 2-morphism 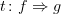 . Then the result of the whiskering is a 2-morphism from
. Then the result of the whiskering is a 2-morphism from 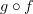 to
to 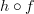 .
.Whiskering on the right can be done in an analogous situation.
-
- CommentRowNumber53.
- CommentAuthorHarry Gindi
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Is there a generalization of whiskering to weak 2-cats? It seemed to be a technique that Vistoli was using even though he was proving things about weak 2-cats (forced by using pseudofunctors).
-
- CommentRowNumber54.
- CommentAuthorTobyBartels
- CommentTimeMar 26th 2010
Sure, you can do whiskering in weak 2-categories.
If you know how to do horizontal composition, then you know how to do whiskering. Whiskering with a morphism
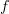 is simply horizontal composition with the identity 2-morphism
is simply horizontal composition with the identity 2-morphism 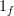 .
. -
- CommentRowNumber55.
- CommentAuthorDavidRoberts
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
>I don't know any way that \mathrm{Cat} is a double category, except the two degenerate ways in which any 2-category may be interpreted as a double category.
(By this I think you mean where either the vertical or horizontal arrows are all trivial)
There are other ways, but not in ways that are special to Cat and work for any 2-category, namely there is the double category of commuting squares and the double category of squares that commute up to a natural transformation - this latter uses whiskering to define horizontal and vertical compositions (see the recent paper by John Baez and John Huerta on the arXiv for some pictures of this, but in a different context) -
- CommentRowNumber56.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Thanks! To you all. Especially to Eric. This is looking much better now. I see real progress going on.
If in the course of this the nLab page adjunction is being prettified and improved, you make me a happy man. If everyone tries to prettify and improve those entries whose content he or she is concerned with, for one reason or other, then eventually we'll get the best possible resource.
by the way, with everyone looking at adjunction: we also have adjoint functor with much more details. This is really more specific to what the discussion has been about! I had intentially tried to keep the 2-category theory out of it and explain adjunctions just of functors.
-
- CommentRowNumber57.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
I added an Idea-section and an Examples-section to adjunction.
-
- CommentRowNumber58.
- CommentAuthorTodd_Trimble
- CommentTimeApr 1st 2010
As I've said elsewhere, I'm just returning to the math blogosphere after spending several weeks away -- and plowing through hundreds and hundreds of comments. So I cannot pretend to have read every one of them with care.
Adjoint functors are perhaps the most important basic notion in all of category theory, so trying to understand them is time well spent. But you need examples before their true significance sinks in. Eric: what examples are you testing your understanding on?
Adjoint functors are pretty hard for most people to understand readily, but it may help if you have an example like "free groups" in hand to guide you along, as you work slowly through (say) the formulation that uses natural bijections between hom-sets. The formulation which uses triangular equations is very pretty, but for me it came at a slightly later stage of understanding. If you do work with that formulation, then again I would recommend that you bring it down to earth, by understanding thoroughly what it is saying in an example like that of "free groups". That can be very enlightening.
You will also want to keep building your stockpile of examples. After a while, you may see adjoint functors just about everywhere you turn. And that can be very powerful.
Most of this discussion, as far as I can tell, has been on getting the "syntax" of adjunctions straightened out. But that's not my memory of how I learned it -- I swallowed it with loads of "semantic sugar"!
-
- CommentRowNumber59.
- CommentAuthorPeter Heinig
- CommentTimeJun 12th 2017
Gave adjunction some polishing here and there.
-
- CommentRowNumber60.
- CommentAuthorTodd_Trimble
- CommentTimeJun 12th 2017
It’s not clear to me that these types of stylistic rewording constitute “polishing” (i.e., improvement), at least not in all places. We each have our individual styles and preferences in expressing ourselves, but unless there is something actually wrong with the English (misspellings, mistakes in grammar, etc.), or something is unclear or ambiguous, then generally out of respect, or not stepping on each others’ toes, we should be a bit circumspect about erasing the style of others and imposing our own. I feel this is an important point to keep in mind when dealing with a collaborative enterprise such as the nLab.
It’s similar to the adage in improv, “yes, and…”.
-
- CommentRowNumber61.
- CommentAuthorPeter Heinig
- CommentTimeJun 12th 2017
- (edited Jun 12th 2017)
Thanks for the extensive feedback.
You are right that the changes are of mixed value.
All were thought to be improvements though.
Still new to nLab, and its general guidelines urge to be bold.
Will adjust my threshold for when to edit further to the side of not editing, though.
For what it’s worth, here’s a run-down (for others: all merely linguistic matters, probably not interesting to read):
“a la the Yoneda lemma” was wrong in that it missed a diacritic and doubled an article (“la the”)
the change from “describable” to “determined” (etc) does indeed distort the meaning given by the previous author, though not in a serious way. This is a debatable change. Did not think long about this, but thought “determined” to be more neutral, abstract and implicit than “describable” (what does it mean to describe a presheaf? a presheaf being determined by something has a clearer meaning). Moreover, in discussions of (proving) the Yoneda lemma, the phrase “being described by the value on the identity” (etc) is often seen. So thought it to be an improvement.
“yields back” sounded wrong to me (not native speaker though) while “to recover a formula” is standard
” the changes of “triangular equations” was motivated by thinking it an improvement to get the links to the article “triangle identities” in. Moreover, “tirangular equations” is not found by the search, and there is a more general issue of constructions like “Lagrange equation” being preferred to “Lagrangian equation”, or, for example, in graph theory, “Hamilton cycle” being preferable to “Hamiltonian cycle”, for example since every cycle is Hamiltonian when seen as a graph on its own, while the modifier “Hamilton” marks it as a separate concept. Similarly, can an equation be “triangular”? Or rather, any equation can be written triangularly.
“perfectly serviceable” seemed too strong, or rather, not clear in its meaning. My changes reintroduced some degree of unclearness by using “viable” and “classical”, which were now removed.
-
- CommentRowNumber62.
- CommentAuthorTodd_Trimble
- CommentTimeJun 12th 2017
Thanks for explaining your thinking; that’s helpful. I may come back to it later. Please keep in mind however #60 as a general precept when making edits. (I know too that I often feel urges to make small changes, especially regarding preferred notation, but I try to keep those urges in check – with varying degrees of success.)
It does seem to me that there is so much else to do than making small stylistic or linguistic adjustments. If you see a possibility of starting an article on an area close to your research interests and that aligns well with what others are doing here, I think that would be appreciated.
-
- CommentRowNumber63.
- CommentAuthorPeter Heinig
- CommentTimeJun 12th 2017
Thanks for the answer.
Minor technical point: my question
what does it mean to describe a presheaf?
was written too hurriedly; I recognize that the previous author did not refer to a presheaf, but to the natural isomorphism Ψ as being desirable to be describeable. If this is what you intended to come back to, there is no need to explain this. That was a mixing up of terms.
1 to 63 of 63