nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Terry Tao's post on MO related to category theory and topology
Bottom of Page1 to 4 of 4
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
So Terry Tao gave an answer on MO earlier, where he said that you can construct Top using sheaves of sets on Set, but he didn't really know how.
Is this actually true? Can we construct Top as a stack on Set without giving the axioms for a topological space (hidden or otherwise)?
-
- CommentRowNumber2.
- CommentAuthorTim_Porter
- CommentTimeMar 25th 2010
Reading that I think he may be referring to Grothendieck topologies.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
So you are thinking of this sentence of Tao's, here:
I believe that there is some equivalent way to axiomatise topology via continuous functions using the machinery of sheaves, which is in some ways more "natural" than the simple but somewhat arbitrary-looking axioms for open sets,
?
This does not mention sheaves on
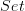 . Did he say something about that elsewhere?
. Did he say something about that elsewhere?Yes, so my impression, too, is that he is simply referring to the sheaf topos on the category of open subsets of a topological space.
But there are of course ways to speak of topologies that are very category-theoretic and don't look like the ordinary definition. For instance a topology on a space is a sub-quantale of the power-set quantale or something like that. (I forget. Maybe sub-*-quantale).
But I think the royal road to topological spaces in terms of just category theory is regarding them as localic toposes. We can say "localic topos" using only very natural category-theoretic language that never looks ad hoc.
-
- CommentRowNumber4.
- CommentAuthorTim_Porter
- CommentTimeMar 25th 2010
Exactly.
1 to 4 of 4