nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Magmoid, semicategory, semifunctor
Bottom of Page1 to 18 of 18
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Proposals for definitions:
Definitions:
Magmoid: A category without (necessarily) identities or associative composition.
Semicategory: A category without (necessarily) identities
Semifunctor: A semifunctor is a functor without the requirement that identities map to identities.
Uses: Categorifies magmas, semigroups, quasigroups, loops.
Semifunctors provide the correct way to describe the map k x {0} -> k x k of rings in the delooping. Note that this is still a meaningful algebraic concept. (For example it explains why localizations behave how they do in a product of fields.)
Are there any opposed or for the motion?
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
Oh yeah, and faithful semifunctors give the right notion for "classes of morphisms that are closed under composition", which means that there should be a use for them in describing localization.
-
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeMar 29th 2010
As always, it's unfortunate that "semigroups" are called that rather than "semimonoids". (-:
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
Are there any opposed or for the motion?
Go ahead.
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
I made them up, so I figured I'd ask.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
Semicategory people have used before, at least.
-
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
I wrote up semipresheaf, semifunctor, and semicategory. I feel like the notion of a magmoid is just for completion and adding it would just be pretty pointless.
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeMar 31st 2010
Given semicategories
 and
and  , a semidiagram is a semifunctor
, a semidiagram is a semifunctor 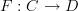 :)
:) -
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeMar 31st 2010
The term "diagram" is not useful, since a diagram is just a functor. Similarly, a semidiagram would just be a semifunctor.
-
- CommentRowNumber10.
- CommentAuthorJacques_Carette
- CommentTimeApr 20th 2010
I am currently (re)developing a lot of algebra, starting from a long list of essentially algebraic theories. To get from one theory to another, and following the Little Theory methodology, I add one item at a time, using coproducts and pushouts. In that setting, the algebraic theory of Magmas is extremely important as it is frequently the 'base' of many pushout diagrams. I expect that, when moving from a 0-categorical view (aka set-based) to seeing things categorically, magmoids would find their proper place.
Mathematically, magmas are completely uninteresting, but as a 'structuring object' for the web of mathematical theories, it is very important. I think of it like the discrete 2 object category; sure as a category it is completely trivial, but as a target for Functors, it is extremely useful!
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeOct 11th 2010
I like the concept of semicategories and would like to learn more about them. Do they go by any other name in the literature? Googling didn’t help me much.
I think they might be relevant for directed spaces.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeOct 11th 2010
I like the concept of semicategories and would like to learn more about them.
If you know what a category is, you don’t need to learn more. You need to forget something.
Do they go by any other name in the literature? Googling didn’t help me much.
Try googling “category without units.”
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeOct 11th 2010
I added to semicategory a section “In higher category theory” with a brief remark.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeOct 11th 2010
expanded the Idea-section at semicategory
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeOct 11th 2010
brought some structure into the TOCs at semicategory, semigroup and semiring, cross-linked the three concepts and added one (random) reference.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeOct 11th 2010
At essentially algebraic theory I moved the statement about the equivalence with locally finiely presentable categories to its own Properties-section.
Going along with that, I added this statement also to locally presentable category.
(I understand the the statement is trivial once we adopt the suitable one of the various equivalent definitions of these concepts, but it is still important to state it and to interlink these two entries)
-
- CommentRowNumber17.
- CommentAuthorTim_Porter
- CommentTimeOct 12th 2010
@Harry One thought resulting from this is : have you looked at Weak Identity Arrows in Higher Categories, Joachim Kock, IMRP Intrnat math. Res. papers, 2006 Article ID69163, p. 1-54. There may be some ideas in there that would be useful. (It is more accessible in a preprint form http://arxiv.org/abs/math/0507116.)
-
- CommentRowNumber18.
- CommentAuthormaxsnew
- CommentTimeOct 3rd 2017
- (edited Oct 3rd 2017)
I added to semifunctor a reference to one application in programming language semantics. Also, I added a statement that semifunctors are equivalent (using choice) to adjoint pairs of distributors. I’ve never seen that theorem in that form anywhere, but it’s basically the same as the well-known theorem when you have a cauchy-complete category.
1 to 18 of 18