Identity morphism can cause problems for commutative diagrams.
I am with those who say that if you draw a loop 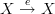 (but not looking like that, since ‘
(but not looking like that, since ‘ ’ should only be written once) and claim that it commutes, then you are claiming that
’ should only be written once) and claim that it commutes, then you are claiming that 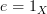 . In particular, an operation on objects and morphisms that preserves all commutative diagrams must preserve identities (and thus be a functor).
. In particular, an operation on objects and morphisms that preserves all commutative diagrams must preserve identities (and thus be a functor).
However, not everything involving an identity morphism can actually be drawn in this way. For example, given 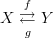 , there's no way to indicate that the composition in one direction is the identity without also catching the other direction. If you tell me that the diagram that I've just drawn commutes, then I'll take it to mean that
, there's no way to indicate that the composition in one direction is the identity without also catching the other direction. If you tell me that the diagram that I've just drawn commutes, then I'll take it to mean that 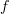 and
and 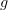 are inverses (although I'll feel more certain if you draw the arrows curved on opposite sides). If you only want one composite to be the identity, then you can either put an identity arrow in explicitly (making a triangle) or adopt a convention that (say) the curved arrow is a section and the straight arrow is the retraction.
are inverses (although I'll feel more certain if you draw the arrows curved on opposite sides). If you only want one composite to be the identity, then you can either put an identity arrow in explicitly (making a triangle) or adopt a convention that (say) the curved arrow is a section and the straight arrow is the retraction.
The reason that I'd feel a little uncomfortable taking that diagram literally (to mean that 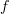 and
and 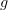 are inverses) is that there's another convention about parallel arrows with no gap between them. For example, if you have
are inverses) is that there's another convention about parallel arrows with no gap between them. For example, if you have 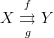 , then to say that the diagram that I've just drawn commutes should mean that
, then to say that the diagram that I've just drawn commutes should mean that 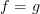 . But in fact, that often appears as a small part of a larger commutative diagram where you don't mean that
. But in fact, that often appears as a small part of a larger commutative diagram where you don't mean that 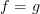 , but simply mean that the diagram commutes with either version. (If you really want to say that
, but simply mean that the diagram commutes with either version. (If you really want to say that 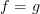 , then again it's better if the arrows are curved on opposite sides.)
, then again it's better if the arrows are curved on opposite sides.)
So in a straightforward mathematical theory of commutative diagrams, then you certainly want a loop to be an identity, 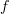 and
and 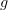 to be inverses in
to be inverses in 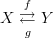 , and
, and 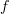 and
and 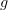 to be equal in
to be equal in 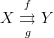 . But in practice, people might adopt conventions that cancel those conclusions.
. But in practice, people might adopt conventions that cancel those conclusions.