I guess this is well known, but let me try writing it here and see what happens.
If a connection on a principal -bundle is locally represented by the 1-form with values in , then the connection is flat if and only if the curvature 2-form vanishes, that is, if is a solution of the Maurer-Cartan equation.
Now, what is interesting is that one can see curvature only on 2-dimensional paths (it is a 2-form): if one restricts to a 1-dimensional submanifold, then there is clearly a solution to the Maurer-Cartan equation. so, if I think of an infinitesimal 1-simplex and look at my connection there, I could say that my connection is 1-flat. then, moving to an infinitesimal 2-simplex I see that the connection is (generally) not 2-flat: holonomy along two sides of the 2-simplex is not the same thing as holonomy along the third side. not the same, but in a very precise way: the curvature exactly measures the gap to go from a horn of the 2-simplex to the third edge. this is very 2-categorical, and suggests I could cure the lack of flatness of my original connection by adding a copy of in degree -1 and cooking up a 2-Lie algebra . Maurer-Cartan equation for this 2-Lie algebra would coincide with the original one one the 1-simplex (since only degree 1 elements are 1-forms with values in . but on the 2-simplex we would have, in addition to these elements, also 2-forms with coefficients in , and the Maurer-Cartan equation on teh simplex would look like where is the differential of the -algebra (and it should be induced by the identity of , thought as a degree 1 map from to ). So the original equation telling that had curvature is now equivalent to say that is flat.
in other words, what seemed a non-flat connection was so since I was not seeing the 2-bundle, but only a 1-bundle approximation. and on a 1-bundle I can only clearly see up to 1-simplices, wher my connection was actually flat.
once curvature has come in, we can repeat the argument: now we have a 2-flat connection and test it on the 3-simplex. if it has 3-curvature, that will presumibly be because we are not seeing the 3-bundle, yet. so I find it natural to wonder (to conjecture) whether any connection on a principal bundle (and more generally any -flat connection on an -bundle) can be seen as a flat connection on an -bundle.
We can “test” all 1-diagrams to see if they 1-commute. If one does not, we can “fill” it with 2-morphisms to make the individual filled 2-diagram 2-commute. Then we can test all subsequent 2-diagrams to see if they 2-commute. If one does not, we can fill it with 3-morphisms to make it 3-commute. Etc etc.
PS: The prescription chosen for “filling” a category like this could be called something like the “-curvature of an -category”, where the category itself is essentially an -connection.
]]>
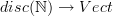 sending
sending  to
to 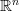 . Then the analogue of what I was talking about in the free category case is all finite dimensional vector spaces, not just the collection of
. Then the analogue of what I was talking about in the free category case is all finite dimensional vector spaces, not just the collection of 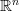 s. Note that
s. Note that 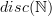 here is the category with set of objects
here is the category with set of objects 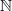 and only identity arrows.
and only identity arrows.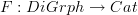 ? I should hope so.
? I should hope so.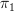 non-trival (for various basepoints if not connected). Then non-equal arrows should correspond to holes in the space. And adding even non-invertible higher arrows plays absolute havoc with the space (well, the homotopy type), because then these add non-trivial homotopy groups in (potentially) an infinite number of dimensions.
non-trival (for various basepoints if not connected). Then non-equal arrows should correspond to holes in the space. And adding even non-invertible higher arrows plays absolute havoc with the space (well, the homotopy type), because then these add non-trivial homotopy groups in (potentially) an infinite number of dimensions.