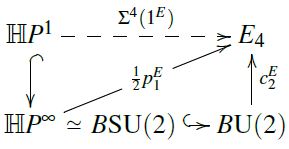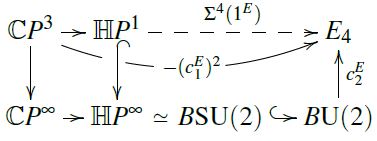The argument in #9, #10 above was not correct (for instance: the same argument would immediately imply that has no ordinary cohomolgy in degree 6…).
The following argument should work. It’s essentially a standard basic argument in complex oriented cohomology theory, and I suppose I am making a fool of myself here in going on about this at all. But here goes:
To recall, the question was:
How to formally show that every complex orientation induces a quaternionic orientation by setting ?
First, a quick abstract way to see it:
Just as complex orientations are co-represented by the ring spectrum (all homotopy-commutative), so quaternionic orientations are co-represented by the ring spectrum (by the same proof, just with the evident substitutions), and the evident map is a ring spectrum homomorphisms. This way complex orientations immediately induce quaternionic representations by precomposition with .
Unravelling this, what is happening under the hood:
Under the equivalence the following two inclusions are equivalent (by this diagram):
the canonical inclusion ;
the canonical inclusion .
The fact that the Conner-Floyd Chern class is a Thom class for complex rank-2 bundles says it restricts to unity along the second of these maps.
But by the equivalence to the first of these maps, it also restricts to unity there, and this was to be shown.
Of course the very same argument run in reverse shows that itself really gives an orientation of complex line bundles. So, nothing to see here, please move along.
]]>