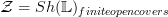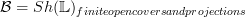okay, thanks Andrew, at least that tells me what's going on.
Was a bad idea to put that novel-like text in a subscript anyway! :-)
So here what I wanted to typeset:
for

the category of smooth loci, consider the Grothendieck topology given by
a) covers are finite open covers
b) covers are finite open covers and projections.
Then sheaves wrt the first yield the smooth topos 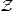 , sheaves with respect to the second the smooth topos
, sheaves with respect to the second the smooth topos 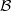 , with notation as in Models for Smooth Infinitesimal Analyis (see list in appendix 2).
, with notation as in Models for Smooth Infinitesimal Analyis (see list in appendix 2).
I tried to add to microlinear space a (the supposedly obvious) proof that all representable objects in these toposes are microlinear.
]]>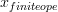 and
and 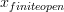 .
.
 ]]>
]]>