I tried to prettify the entry infinitesimal object:
I expanded and restructured the "Idea" section. I tried to emphasize the point that Lawvere's axioms are the right general point of view and that the wealth of constructions in algebraic geoemtry is, from this abstract nonsense point of view, to be regarded as taking place in a model for these axioms. I cite Anders Kocks's latest book for the most simple minded version of how algebraic geometry is a model for sdg, but I think this goes through for more sophisticated versions, too. It would be nice to discuss this eventually elsewhere in some entry on "algebraic geometry as models for smooth toposes".
I have also tried to subsume the approach of nonsstandard analysis as yet another special case of Lawvere's general axioms, by referring to Moerdijk-Reyes' topos 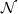 and
and 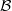 in which "objects of invertible infinitesimals/infinities" exist and model nonstandard analysis. This, too, would deserve being expanded on further, but I am thinking for the nLab this abstract-nonsense-first perspective is the right one.
in which "objects of invertible infinitesimals/infinities" exist and model nonstandard analysis. This, too, would deserve being expanded on further, but I am thinking for the nLab this abstract-nonsense-first perspective is the right one.
Then I inserted some links to the now separate infinitesiaml interval object that I am still working on. I also changed the ideosyncratic terminology "infinitesimal k-cube" and "infinitsimal k-disk" to "cartesian product of inf. intervals" and "k-dimensional infinitesimal interval". Anders Kock calls the latter a "monad", following Leibniz, but I am hesitating to overload monad this way, given that Kock's use of it doesn't seem to be wide spread.
]]>