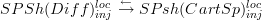Thanks for the comments.
I came to wonder about this in thinking about how to get the naive formula for an external tensor product to yield a derivable functor on an integral model structure. In some natural contexts I can see that it behaves like a left Quillen functor on an ambient integral model structure except that (or if only) the initial operation of pullback of either factor to the cartesian product of their bases spaces is or were left Quillen wrt the projective model strcuture.
But this fails badly over sites of simplicial groupoids, since here cofibrancy essentially means free actions of the simplicial Kan loop group, and the partially trivial actions obtained by pullback along projections are as far from this as possible. In view of this, last night, I naively came to wonder whether if I’d pull a Thomason-trick and removed all manifest automorphisms by passing to posetal models of homotopy types I could get around this problem. But now I see that this is hopeless.
As another solution to the problem I guess one could pick a “universe” of simplicial group that one cares about, then blow up the point space to (using here that has itself group structure) and blow up any connected homotopy type that one cares about to , thought of as sliced over the blown-up point via the inclusion (using that this is in fact a group homomorphism) and the identity on all the other factors.
This way, every cofibrant object parameterized by the blow-up of is now freely acted on by all (the and hence) the in the universe. Moreover, the product over the blown-up point of the blow-up of with another is now such that pullback to it along either of the two projections amounts to restricting, in the left factor, say, -actions along the inclusions , which does preserve cofibrancy.
]]>