created a section on cofibrations in CdgAlg and hence on Sullivan algebras.
Created entry for Dennis Sullivan in that context. Always nice to create an entry and see that the "timeline"-entry was already requesting it.
I suppose I'll have the following sorted out in a minute, but maybe somebody is quicker with helping me:
in the definition of a relative Suillvan algebra 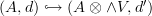 I suppose we do require that
I suppose we do require that 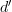 restricted to
restricted to 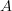 acts like
acts like 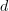 plus a term that contains elements in V ?
plus a term that contains elements in V ?