At Existence of Bousfield localization I spelled out the proof (from Barwick's article) that every left proper combinatorial model category has all Bousfield localizaitons at sets of morphisms. Using Jeff Smith's recognition theorem for combinatorial model categories, this is comparatively easy.
But I seem to have one confusion about filtered colimits:
Question
Why is every  -filtered colimit in a model category necessarily a homotopy colimit, for sufficiently large
-filtered colimit in a model category necessarily a homotopy colimit, for sufficiently large  ?
?
I seem to have a worse confusion, which probably shows that I am suffering from an elementary misundersstanding of something:
at small object it says that that a  -compact obect for regular
-compact obect for regular  is also compact for all
is also compact for all 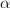 greater than
greater than  . But clearly also for all
. But clearly also for all 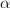 lower than
lower than  . So for all
. So for all 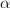 ? What's wrong here??
? What's wrong here??
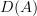 and
and 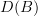 I suppose you mean the model categories of complexes insteadof the derived categories? Otherwise I am not sure what Bousfield localization should mean, for derived categories.
I suppose you mean the model categories of complexes insteadof the derived categories? Otherwise I am not sure what Bousfield localization should mean, for derived categories.