removed from cofibrantly generated model category the extra section on presentable ones, which became superfluous after Mike (if I saw correctly) added the clause that generating cofibrations and acyclic cofibrations admit the small object aregument.
Instead, I moved now the statement that 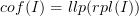 below the main definition and supplied the details of the proof
below the main definition and supplied the details of the proof